2023-2024学年初中数学人教版七年级下学期 第六章 实数 单元测试 A卷
试卷更新日期:2024-03-15 类型:单元试卷
一、选择题
-
1. 9的算术平方根是( )A、 B、 C、 D、2. 下列各数中的无理数是( )A、 B、 C、0 D、3. 的立方根是( )A、 B、2 C、 D、44. 下列各数中,界于6和7之间的数是( )A、 B、 C、 D、5. 下列说法中,正确的是( )A、正整数和负整数统称整数 B、整数和分数统称有理数 C、零既可以是正整数,也可以是负整数 D、一个有理数不是正数就是负数6. 下列四个实数中,属于无理数的是( )A、 B、 C、 D、7. 有下列四个命题:①相等的角是对顶角;②两条直线被第三条直线所截,同位角相等;③无理数包括正无理数、0、负无理数;④同一平面内,垂直于同一条直线的两条直线平行.是真命题的命题的个数有( )个.A、1 B、2 C、3 D、48. 实数的值在( )A、和之间 B、和之间 C、和之间 D、和之间9. 数轴上点所表示的实数可能是( )
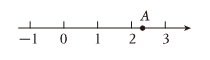 A、 B、 C、 D、10. 满足的整数有几个?( )A、3 B、4 C、5 D、6
A、 B、 C、 D、10. 满足的整数有几个?( )A、3 B、4 C、5 D、6二、填空题
-
11. 的平方根是 .12. 根据下表回答: .13. 比较大小: .14. 请写出一个比﹣ 小的无理数:.15. 一个正数的平方根是和 , 求这个正数 .
三、计算题
-
16. 计算:17. 计算:18. 计算:
四、解答题
-
19. 已知:和是的两个不同的平方根,是的立方根求、、的值.20. 已知一个正数的平方根分别是和 , 又的立方根为 .(1)、求a , b的值;(2)、求的算术平方根.
五、实践探究题
-
21. 阅读材料:
∵<< , 即2<<3,
∴0<-2<1,
∴的整数部分为2,的小数部分为-2.
解决问题:
(1)、填空:的小数部分是 ;(2)、已知a是的整数部分,b是的小数部分,求a+b-的立方根.22. 请认真阅读下面的材料,再解答问题.依照平方根(即二次方根)和立方根(即三次方根)的定义,可给出四次方根、五次方根的定义.
比如:若 , 则叫的二次方根;若 , 则叫的三次方根;若 , 则叫的四次方根.
(1)、依照上面的材料,请你给出五次方根的定义;(2)、81的四次方根为;-32的五次方根为;(3)、若有意义,则的取值范围是;若有意义,则的取值范围是;(4)、求的值: .23. 我们知道,负数没有算术平方根,但对于三个互不相等的负整数,若两两乘积的算术方根都是整数,则称这三个数为“完美组合数”.例如:-9,-4,-1这三个数, , , ,其结果6,3,2都是整数,所以-1,-4,-9这三个数称为“完美组合数”.
(1)、-18,-8,-2这三个数是“完美组合数”吗?请说明理由.(2)、若三个数-3,m , -12是“完美组合数”,其中有两个数乘积的算术平方根为12,求m的值.