2023-2024学年初中数学人教版七年级下学期 第五章 相交线与平行线 单元测试 B卷
试卷更新日期：2024-03-15 类型：单元试卷
一、选择题
-
1. 如图是小周同学在校运会上投掷实心球的场景，当投掷完毕时，测量员选取AB的长度作为小周的成绩，其依据是（ ）．
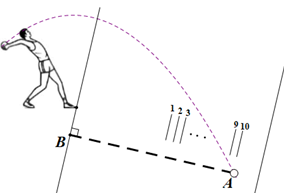A、垂线段最短 B、两点之间线段最短 C、两点确定一条直线 D、过一点有且只有一条直线与已知直线垂直2. 直线、线段、射线的位置如图所示，下图中能相交的是（ ）A、
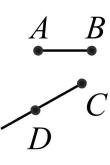B、
C、
D、
3. 在下列命题中，是真命题的是（ ）A、相等的角是对顶角 B、若 ， 则 C、两个锐角的和是钝角 D、有两个角相等的三角形是等腰三角形4. 如图，直线 ， 的直角顶点A落在直线a上，点B落在直线b上，若 ， ， 则的大小为（ ）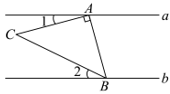
A、50° B、45° C、40° D、35°5. 如图，下列条件中能判定是（ ）
A、 B、 C、 D、6. 如图，将网格中的三条线段沿网格线的方向(水平或竖直)平移后组成一个首尾依次相接的三角形，至少需要移动 （ ）
A、12格 B、11格 C、9 格 D、8格7. 下列图形中，周长最长的是（ ）A、
B、
C、
D、
8. 如图，A，B，C，D中的哪幅图案可以通过图案①平移得到（ ）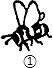
A、
B、
C、
D、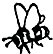
9. 过直线l外一点P作直线l的平行线，下列尺规作图中，错误的是（ ）A、
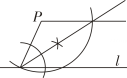B、
C、
D、
10. 如图1，当光从空气进入水中时，会发生折射，满足入射角∠1 与折射角∠2 的度数比为4：3.如图2，在同一平面上，两条光线同时从空气进入水中，两条入射光线与水面的夹角分别为α，β，水中两条折射光线的夹角为γ，则α，β，γ三者之间的数量关系为（ ）
A、 B、 C、α+β=γ D、二、填空题
-
11. “平行于同一条直线的两条直线平行”是 命题（填“真”或“假”）．12. 如图1，一块长为a(cm)，宽为b(cm)的长方形地板中间有一条裂缝.如图2，若把裂缝右边的一块向右平移x(cm)，则产生的裂缝的面积为cm2.
13. 如图，平面反光镜AC斜放在地面AB上，一束光线从地面上的P点射出，DE是反射光线.已知∠APD=120°，若要使反射光线DE∥AB，则∠CAB应调节为°(提示：∠ADP=∠CDE，三角形的内角和等于180°).
14. 如图，直线AB，CD交于点O，∠AOC：∠COE=1：2．若∠BOD=28°，则∠COE等于度．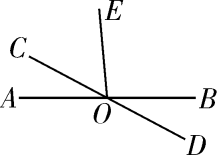
15. 如图，将长方形纸片 ABCD沿EF折叠后，点A，B分别落在A'，B'的位置，再沿AD边将∠A'折叠到∠H处，若∠1=52°，则∠AEF= ， ∠FEH= .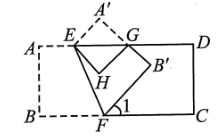
三、作图题
-
16. 如图，已知直线l和l外一点P，用尺规作l的垂线，使它经过点P.（保留作图痕迹，不写作法）
17. 如图，在∠AOB 内有一点 P.
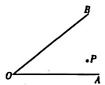(1)、过点 P 作l1∥OA.(2)、过点 P 作l2∥OB.(3)、用量角器量一量 l1 与 l2 的夹角与∠O 有怎样的数量关系?四、解答题
-
18. 如图，已知直线AB与CD相交于点O，OD平分∠BOE，∠AOE＝126°．
(1)、求∠AOC的度数.(2)、若直线OF⊥OE，求∠DOF的度数.五、实践探究题
-
19. 如图
(1)、【感知】已知：如图①，点E在AB上，且CE平分∠ACD，∠1＝∠2．求证：AB∥CD．将下列证明过程补充完整：
证明：∵CE平分∠ACD（已知），
∴∠2＝∠ ▲ （角平分线的定义），
∵∠1＝∠2（已知），
∴∠1＝∠ ▲ （等量代换），
∴AB∥CD（ ）．
(2)、【探究】已知：如图②，点E在AB上，且CE平分∠ACD，AB∥CD．求证：∠1＝∠2．(3)、【应用】如图③，BE平分∠DBC，点A是BD上一点，过点A作AE∥BC交BE于点E，∠ABC：∠BAE＝4：5，直接写出∠E的度数．20. 【教材呈现】如图是华师版七年级上册数学教材第176页的部分内容．有了“两直线平行，同位角相等”，我们就能用推理的方法得出“两条平行线被第三条直线所截，内错角相等”．
如图①，已知平行线a、b被直线l所截，我们将∠1的对顶角记为∠3．
(1)、下面是“两直线平行，内错角相等”的推理过程，在括号内填写理由．∵a∥b（ ），
∴∠2＝∠3（ ）．
∵∠1＝∠3（ ），
∴∠1＝∠2（ ）．
(2)、【拓展应用】如图②，AB∥CD，BC∥DE，若∠B＝47°，则∠D＝°．(3)、如图③，已知AB∥CD，∠1＝∠2，试说明∠BEF＝∠EFC．21. 小明完成作业后在家复习，他看到七下课本第12页例4，感到这个结论十分有趣，便尝试探究起来.
(1)、【基础巩固】与例4条件和结论互换，改成了：“如图1，AP 平分∠BAC，CP平分∠ACD，AB∥CD，则∠1+∠2=90°，”小明认为这个结论正确，你赞同他的想法吗? 请说明理由.
(2)、【尝试探究】小明发现：若将其中一条角平分线改成AC的垂线，则“∠1+∠2=90°”这个结论不成立.请帮小明完成探究：
如图2，AB∥CD，AP平分∠BAC，CP⊥AC，∠1是AP与AB的夹角，∠2 是CP与CD的夹角.
①若∠2=22°，求∠1的度数.
②试说明：2∠1-∠2=90°.
(3)、【拓展提高】如图3，若AB∥CD，AP⊥AC，CP平分∠ACD，请直接写出∠1与∠2的数量关系.
六、综合题
-
22. 已知：点E在线段间（如图1）．连接 ． ．
(1)、求证： ．(2)、如图2，点F在点E右侧．连接 ． 求证 ．(3)、如图3在（2）的条件下，线段 ， 的延长线交于点H ． 交于点K ． 当平分 ， 平分 ， ， 时，求的度数．23. 如图1，已知两条直线被直线所截，分别交于点E，点F，平分交于点M，且 ．
(1)、判断直线与直线是否平行，并说明理由；(2)、如图2，点G是射线上一动点（不与点M，F重合），平分交于点H，过点H作于点N，设 ．①当点G在点F的右侧时，若 ， 求的度数；
②当点G在运动过程中，和之间有怎样的数量关系？请写出你的猜想，并加以证明．
-