2023-2024学年初中数学人教版七年级下学期 第五章 相交线与平行线 单元测试 A卷
试卷更新日期：2024-03-15 类型：单元试卷
一、选择题
-
1. 2022年，中国举办了第二十四届冬季奥林匹克运动会，如图，通过平移左图吉祥物“冰墩墩”可以得到的图形是（ ）
A、
B、
C、
D、
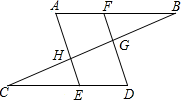
2. 如图，在下面4个图形中，∠1与∠2属于同位角的是（ ）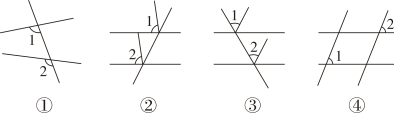
A、① B、①② C、①③ D、②③④3. 如图，下列条件中，能判定AB∥EF的是（ ）
①∠B+∠BFE=180°；
②∠1=∠2；③∠3=∠4；
④∠B=∠5.A、② B、①③ C、①③④ D、②③④4. 如图，直线DE∥FG，三角尺ABC的顶点B，C分别在DE，FG上.若∠BCF=25°，则∠ABE的度数为（ ）
A、25° B、55° C、65° D、75°5. 如图，要把河中的水引到村庄A，小凡先作AB⊥CD，垂足为点B，然后沿AB开挖水渠，就能使所开挖的水渠最短，其依据是（ ）
A、两点确定一条直线 B、两点之间线段最短 C、直线外一点与直线上各点连接的所有线段中，垂线段最短 D、在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线6. 根据投影屏上出示的填空题，判断下列说法正确的是 （ ）已知：如图是△ABC.
试说明：∠BAC+∠B+∠C=180°.
解：过点A作DE∥ ◎ .
∴∠DAB=∠B，∠EAC= ＠ .
又∵∠DAB+∠BAC+∠EAC= ▲ .
∴ ※ +∠BAC+∠C=180°.
A、◎代表 AB B、@代表∠BAC C、▲代表 90° D、※代表∠B7. 如图，已知AB∥EG，BC∥DE，CD∥EF，则x，y，z三者之间的关系是 （ ）
A、x+y+z=180° B、x-z=y C、y-x=z D、y -x=x-z8. 如图，直线m∥n，∠1=100°，∠2=30°，则∠3 的度数为 （ ）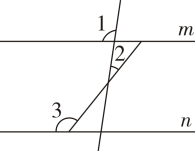
A、70° B、110° C、130° D、150°9. 如图，若 ， ， ， 则的度数为（ ）
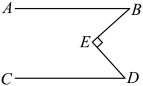A、 B、 C、 D、10. 如图，已知 ， ， 点P是射线上一动点（与点A不重合），、分别平分和 ， 分别交射线于点C、D，下列结论：①；②；③当时，；④当点P运动时，的数量关系不变．其中正确结论有（ ）个
A、1 B、2 C、3 D、4二、填空题
-
11. 将“平行于同一条直线的两条直线平行”改写成“如果……那么……”的形式为.12. 在如图所示的方格纸中，AB∥ ， AB⊥.
13. 如图，已知AB∥CE，∠B=50°，CE平分∠ACD，则∠ACD的度数为°.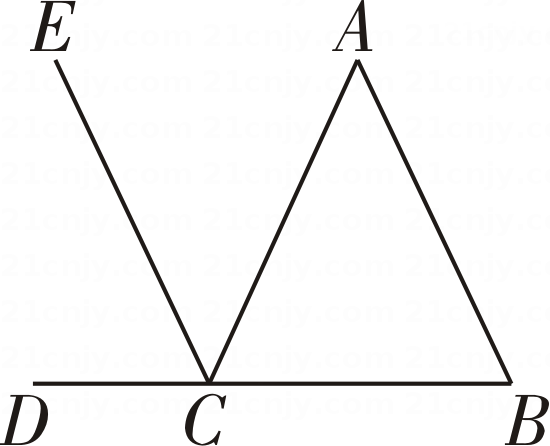
14. 如图是一块长方形的场地，长AB=a(m)，宽AD=b(m).已知从A，B两处入口的小路宽都为1m，两小路汇合处路宽为2m，其余部分种植草坪，则草坪的面积为m².
15. 如图，三角形ABC的边BC长为4cm.将三角形ABC平移2cm得到三角形A'B'C'，且BB'⊥BC，则阴影部分的面积为cm².
三、解答题
-
16. 如图，已知∠1=∠2，∠AED+∠BAE=180°，试问：∠F和∠G相等吗？请说明理由.
17. 如图，把一张长方形纸片ABCD沿EF折叠，点D，C分别落在D'，C的位置上，ED'的延长线与BC交于点G．若∠EFG= 63°，求∠1，∠2的度数．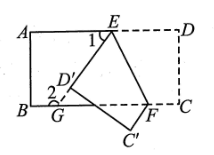
18. 如图，已知AB∥DE，∠1=18°，∠2=125°，求∠BCD的度数.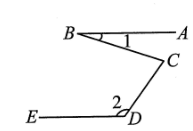
四、实践探究题
-
19. 探究：如图 ， ， ， 若 ， 求的度数．
请将下面的解答过程补充完整，并填空．
解：因为 ，
所以 ▲ （ ）.
因为 ，
所以 ▲ （ ）.
所以等量代换 ．
因为 ，
所以 ▲
应用：如图 ， ， ， 若 ， 求的度数．
20. 已知：如图是一个跳棋棋盘，游戏规则是：一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角。跳动时，每-步只能跳到它的同位角或内错角或同旁内角的位置上，例如：从起始角∠1跳到终点角∠3写出其中两种不同路径，路径1：∠1∠9∠3．
路径2：∠1∠12∠6∠10∠3．
试一试：
(1)、从起始角∠1跳到终点角∠8；(2)、从起始角∠1依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点角∠8？21. 某学习小组发现一个结论：已知直线a∥b，若直线c∥a，则c∥b.他们发现这个结论应用很广，请你利用这个结论解决以下问题：已知直线 AB∥CD，点E在AB，CD 之间，点 P，Q分别在直线AB，CD上，连结 PE，EQ.
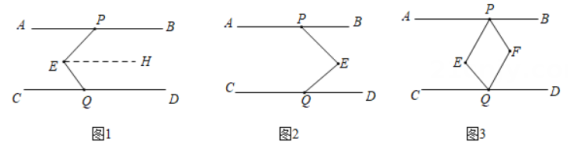(1)、如图1，过点 E 作 EH∥AB，运用上述结论，探究∠PEQ，∠APE，∠CQE之间的数量关系，并说明理由.(2)、如图2，类比(1)中的方法，运用上述结论，探究∠PEQ，∠APE，∠CQE 之间的数量关系，并说明理由.(3)、如图3，PF 平分∠BPE，QF 平分∠EQD，当∠PEQ=140°时，请直接写出∠PFQ的度数.五、综合题
