2014年高考理数真题试卷（江苏卷）

试卷更新日期：2016-09-28 类型：高考真卷

进入出卷网下载

一、填空题

1. 已知集合A={﹣2，﹣1，3，4}，B={﹣1，2，3}，则A∩B= ．

查看试题解析
2. 已知复数z=（5+2i）²（i为虚数单位），则z的实部为．

查看试题解析
3.
如图是一个算法流程图，则输出的n的值是．

查看试题解析
4. 从1，2，3，6这4个数中一次随机抽取2个数，则所取2个数的乘积为6的概率是．

查看试题解析
5. 已知函数y=cosx与y=sin（2x+φ）（0≤φ＜π），它们的图象有一个横坐标为 $\frac{π}{3}$ 的交点，则φ的值是．

查看试题解析
6. 为了了解一片经济林的生长情况，随机抽测了其中60株树木的底部周长（单位：cm），所得数据均在区间[80，130]上，其频率分布直方图如图所示，则在抽测的60株树木中，有株树木的底部周长小于100cm．

查看试题解析
7. 在各项均为正数的等比数列{a_n}中，若a₂=1，a₈=a₆+2a₄ ，则a₆的值是．

查看试题解析
8. 设甲、乙两个圆柱的底面积分别为S₁ ， S₂ ，体积分别为V₁ ， V₂ ，若它们的侧面积相等，且 $\frac{S_{1}}{S_{2}}$ = $\frac{9}{4}$ ，则 $\frac{V_{1}}{V_{2}}$ 的值是．

查看试题解析
9. 在平面直角坐标系xOy中，直线x+2y﹣3=0被圆（x﹣2）²+（y+1）²=4截得的弦长为．

查看试题解析
10. 已知函数f（x）=x²+mx﹣1，若对于任意x∈[m，m+1]，都有f（x）＜0成立，则实数m的取值范围是．

查看试题解析
11. 在平面直角坐标系xOy中，若曲线y=ax²+ $\frac{b}{x}$ （a，b为常数）过点P（2，﹣5），且该曲线在点P处的切线与直线7x+2y+3=0平行，则a+b的值是．

查看试题解析
12. 如图，在平行四边形ABCD中，已知AB=8，AD=5， $\vec{C P}$ =3 $\vec{P D}$ ， $\vec{A P}$ • $\vec{B P}$ =2，则 $\vec{A B}$ • $\vec{A D}$ 的值是．

查看试题解析
13. 已知f（x）是定义在R上且周期为3的函数，当x∈[0，3）时，f（x）=|x²﹣2x+ $\frac{1}{2}$ |，若函数y=f（x）﹣a在区间[﹣3，4]上有10个零点（互不相同），则实数a的取值范围是

查看试题解析
14. 若△ABC的内角满足sinA+ $\sqrt{2}$ sinB=2sinC，则cosC的最小值是．

查看试题解析

二、解答题

15. 已知α∈（ $\frac{π}{2}$ ，π），sinα= $\frac{\sqrt{5}}{5}$ ．

(1)、求sin（ $\frac{π}{4}$ +α）的值；

(2)、求cos（ $\frac{5 π}{6}$ ﹣2α）的值．

查看试题解析
16. 如图，在三棱锥P﹣ABC中，D，E，F分别为棱PC，AC，AB的中点，已知PA⊥AC，PA=6，BC=8，DF=5．求证：

(1)、直线PA∥平面DEF；

(2)、平面BDE⊥平面ABC．

查看试题解析
17. 如图，在平面直角坐标系xOy中，F₁ ， F₂分别为椭圆 $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左、右焦点，顶点B的坐标为（0，b），连接BF₂并延长交椭圆于点A，过点A作x轴的垂线交椭圆于另一点C，连接F₁C．

(1)、若点C的坐标为（ $\frac{4}{3}$ ， $\frac{1}{3}$ ），且BF₂= $\sqrt{2}$ ，求椭圆的方程；

(2)、若F₁C⊥AB，求椭圆离心率e的值．

查看试题解析
18. 如图，为保护河上古桥OA，规划建一座新桥BC，同时设立一个圆形保护区，规划要求：新桥BC与河岸AB垂直；保护区的边界为圆心M在线段OA上并与BC相切的圆，且古桥两端O和A到该圆上任意一点的距离均不少于80m，经测量，点A位于点O正北方向60m处，点C位于点O正东方向170m处（OC为河岸），tan∠BCO= $\frac{4}{3}$ ．

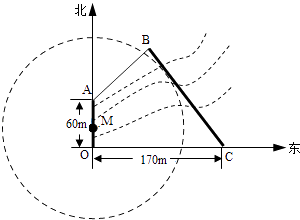(1)、求新桥BC的长；

(2)、当OM多长时，圆形保护区的面积最大？

查看试题解析
19. 已知函数f（x）=e^x+e^﹣^x ，其中e是自然对数的底数．

(1)、证明：f（x）是R上的偶函数；

(2)、若关于x的不等式mf（x）≤e^﹣^x+m﹣1在（0，+∞）上恒成立，求实数m的取值范围；

(3)、已知正数a满足：存在x₀∈[1，+∞），使得f（x₀）＜a（﹣x₀³+3x₀）成立，试比较e^a^﹣¹与a^e^﹣¹的大小，并证明你的结论．

查看试题解析
20. 设数列{a_n}的前n项和为S_n ，若对任意的正整数n，总存在正整数m，使得S_n=a_m ，则称{a_n}是“H数列”．

(1)、若数列{a_n}的前n项和为S_n=2ⁿ（n∈N^*），证明：{a_n}是“H数列”；

(2)、设{a_n}是等差数列，其首项a₁=1，公差d＜0，若{a_n}是“H数列”，求d的值；

(3)、证明：对任意的等差数列{a_n}，总存在两个“H数列”{b_n}和{c_n}，使得a_n=b_n+c_n（n∈N^*）成立．

查看试题解析

三、附加题（本大题包括选做题和必做题两部分）（一）选择题（本题包括21、22、23、24四小题，请选定其中两个小题作答，若多做，则按作答的前两个小题评分）【选修4-1：几何证明选讲】

21. 如图，AB是圆O的直径，C，D是圆O上位于AB异侧的两点，证明：∠OCB=∠D．

查看试题解析
22. 已知矩阵A= $[\begin{matrix} - 1 & 2 \\ 1 & x \end{matrix}]$ ，B= $[\begin{matrix} 1 & 1 \\ 2 & - 1 \end{matrix}]$ ，向量 $\vec{α}$ = $[\begin{matrix} 2 \\ y \end{matrix}]$ ，x，y为实数，若A $\vec{α}$ =B $\vec{α}$ ，求x+y的值．

查看试题解析
23. 在平面直角坐标系xOy中，已知直线l的参数方程为 ${\begin{matrix} x = 1 - \frac{\sqrt{2}}{2} t \\ y = 2 + \frac{\sqrt{2}}{2} t \end{matrix}$ （t为参数），直线l与抛物线y²=4x相交于A，B两点，求线段AB的长．

查看试题解析
24. 已知x＞0，y＞0，证明（1+x+y²）（1+x²+y）≥9xy．

查看试题解析
25. 盒中共有9个球，其中有4个红球，3个黄球和2个绿球，这些球除颜色外完全相同．

(1)、从盒中一次随机取出2个球，求取出的2个球颜色相同的概率P；

(2)、从盒中一次随机取出4个球，其中红球、黄球、绿球的个数分别记为x₁ ， x₂ ， x₃ ，随机变量X表示x₁ ， x₂ ， x₃中的最大数，求X的概率分布和数学期望E（X）．

查看试题解析
26. 已知函数f₀（x）= $\frac{\sin x}{x}$ （x＞0），设f_n（x）为f_n_﹣₁（x）的导数，n∈N^* ．

(1)、求2f₁（ $\frac{π}{2}$ ）+ $\frac{π}{2}$ f₂（ $\frac{π}{2}$ ）的值；

(2)、证明：对任意n∈N^* ，等式|nf_n_﹣₁（ $\frac{π}{4}$ ）+ $\frac{π}{4}$ f_n（ $\frac{π}{4}$ ）|= $\frac{\sqrt{2}}{2}$ 都成立．

查看试题解析