广东省惠州市2023年八年级（上）期末质量监测模拟卷

试卷更新日期：2024-03-15 类型：期末考试

进入出卷网下载

一、选择题（共10小题，满分30分，每小题3分）

1. 2022年卡塔尔世界杯是自1930年以来举办的第22届世界杯，历届世界杯可谓各具特色，会徽设计也蕴含了不同的文化.下列世界杯会徽的图案中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各组线段中，能构成三角形的是（）

A、2，5，8 B、3，3，6 C、3，4，5 D、4，5，9

查看试题解析
3. 点M（﹣4，3）关于x轴对称点的坐标为（）

A、（4，3） B、（4，﹣3） C、（﹣4，3） D、（﹣4，﹣3）

查看试题解析
4. 下列运算正确的是（　　）

A、a¹²÷a⁴＝a³ B、（﹣4x³）³＝4x⁶ C、（x+7）²＝x²+49 D、a⁷•a⁵＝a¹²

查看试题解析
5. 正十二边形的外角和为（）

A、30° B、150° C、360° D、1800°

查看试题解析
6. 下列分式中是最简分式的是（）

A、 $\frac{2 x}{4 x^{2}}$ B、 $\frac{x^{2} + y^{2}}{x + y}$ C、 $\frac{x^{2} + 2 x + 1}{x + 1}$ D、 $\frac{x^{2} - 4}{x + 2}$

查看试题解析
7. 如图，已知AB＝DC，若用定理SSS证明△ABC≌△DCB，则需要添加的条件是（）

A、OA＝OD B、AC＝DB C、OB＝OC D、BC＝CB

查看试题解析
8. 如图，AB＝AC，∠BAC＝100°，AB的垂直平分线交BC于点D，那么∠ADC的度数为（）

A、120° B、30° C、60° D、80°

查看试题解析
9. 如图（1），在边长为a的正方形中挖去一个边长为b的小正方形（a＞b），把余下的部分拼成一个长方形，如图（2），此过程可以验证（）

A、（a+b）²＝a²+2ab+b² B、（a﹣b）²＝a²﹣2ab+b² C、a²﹣b²＝（a+b）（a﹣b） D、（a+b）²＝（a﹣b）²+4ab

查看试题解析
10. 如图，在△ABC中，以点B为圆心，AB为半径画弧交BC于点D，以点C为圆心，AC为半径画弧交BC于点E，连接AE，AD．设∠EAD＝α，∠ACB＝β，则∠B的度数为（）

A、α﹣ $\frac{β}{2}$ B、2α﹣β C、α+ $\frac{β}{2}$ D、3α﹣β

查看试题解析

二、填空题（共6小题，满分18分，每小题3分）

11. 一种植物果实像一个微笑的无花果，质量只有0.000000076克，该质量请用科学记数法表示克．

查看试题解析
12. 分解因式：x²﹣1= ．

查看试题解析
13. 要使分式 $\frac{2 x}{x - 1}$ 有意义，则x应满足的条件是．

查看试题解析
14. 若等腰三角形的两边长分别是3和7，则它的周长是．

查看试题解析
15. 若（x+1）（x﹣2）＝x²+mx﹣n，则mn的值为．

查看试题解析
16. 如图，△ABC为等腰直角三角形AC＝BC，若A（﹣3，0），C（0，2），则点B的坐标为．

查看试题解析

三、解答题（共9小题，满分72分）

17. 如图，C为BE上一点，AB∥DE，AB=CE，∠BAC=∠ECD．求证：AC=CD。

查看试题解析
18. 解方程： $\frac{x}{x - 3} + \frac{6}{x + 3} = 1$

查看试题解析
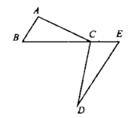19. 先化简，再求值：（2x+3y）²﹣（2x+y）（2x﹣y），其中x＝ $\frac{1}{3}$ ， y＝ $\frac{1}{2}$ ．

查看试题解析
20. 甲乙二人做某种机械零件，已知甲每小时比乙多做6个，甲做90个所用时间与乙做60个所用时间相等．求甲、乙每小时各做多少个零件？

查看试题解析
21. 设A= $(m - \frac{9}{m}) \div \frac{m - 3}{2 m}$ ．

(1)、化简A；

(2)、若x²+mx+16是一个完全平方式，求A的值．

查看试题解析
22. 如图，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．

(1)、作出△ABC关于y轴的对称图形△A'B'C'；

(2)、写出点A'，B'，C'的坐标．

(3)、在y轴上找一点P，使PA+PC的长最短．

查看试题解析
23. 如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．
求证：

(1)、BC＝AD；

(2)、△OAB是等腰三角形．

查看试题解析
24. 阅读下列解题过程：
已知 $\frac{x}{x^{2} + 1}$ = $\frac{1}{3}$ ，求 $\frac{x^{2}}{x^{4} + 1}$ 的值．
解：由 $\frac{x}{x^{2} + 1}$ = $\frac{1}{3}$ ，知x≠0，∴ $\frac{x^{2} + 1}{x} = 3$ ，即x+ $\frac{1}{x}$ =3．
∴ $\frac{x^{4} + 1}{x^{2}} = x^{2} + \frac{1}{x^{2}} = {(x + \frac{1}{x})}^{2} - 2$ ＝3²﹣2＝7，∴ $\frac{x^{2}}{x^{4} + 1}$ = $\frac{1}{7}$ ．
以上解法中，是先将已知等式的两边“取倒数”，然后求出所求式子倒数的值，我们把此题的这种解法叫做“倒数法”，请你利用“倒数法”解决下面问题：

(1)、已知 $\frac{x}{x^{2} - x + 1}$ = $\frac{1}{7}$ ，求 $\frac{x^{2}}{x^{4} + x^{2} + 1}$ 的值；

(2)、已知 $\frac{x y}{x + y}$ =2， $\frac{y z}{y + z}$ = $\frac{4}{3}$ ， $\frac{x z}{x + z}$ = $\frac{4}{3}$ ，求 $\frac{x y z}{x y + y z + z x}$ 的值．

查看试题解析
25.

(1)、问题发现：如图①，△ABC和△EDC都是等边三角形，点B、D、E在同一条直线上，连接AE．
①∠AEC的度数为；
②线段AE、BD之间的数量关系为；

(2)、拓展探究：如图②，△ABC和△EDC都是等腰直角三角形、∠ACB＝∠DCE＝90°，点B、D、E在同一条直线上，CM为△EDC中DE边上的高，连接AE，试求∠AEB的度数及判断线段CM、AE、BM之间的数量关系，并说明理由；

(3)、解决问题：如图③，△ABC和△EDC都是等腰三角形，∠ACB＝∠DCE＝36°，点B、D，E在同一条直线上，请直接写出∠EAB+∠ECB的度数．

查看试题解析