广西壮族自治区来宾市2023-2024学年八年级上学期1月月考数学试题

试卷更新日期：2024-03-15 类型：月考试卷

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑）

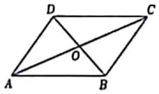
1. 下列代数式中，是分式的为（）

A、 $\frac{x}{3}$ B、 $\frac{y}{π}$ C、 $\frac{2}{3} x$ D、 $\frac{2}{x - 3}$

查看试题解析
2. 数轴上所有的点表示的数是（）

A、全体有理数 B、全体无理数 C、全体实数 D、全体正数和全体负数

查看试题解析
3. 要使分式 $\frac{x}{x - 2}$ 有意义，x的取值范围是（）

A、 $x > 0$ B、 $x < 2$ C、 $x \neq 0$ D、 $x \neq 2$

查看试题解析
4. 已知某种植物花粉的直径约为0.00035米，这个数用科学记数法表示是（）

A、 $3.5 \times 1 0^{4}$ 米 B、 $3.5 \times 1 0^{- 4}$ 米 C、 $3.5 \times 1 0^{- 5}$ 米 D、 $3.5 \times 1 0^{- 6}$ 米

查看试题解析
5. 若 $m > n$ ，则下列不等式正确的是（）

A、 $2 - m < 2 - n$ B、 $3 m < 3 n$ C、 $m + 6 < n + 6$ D、 $\frac{m}{4} < \frac{n}{4}$

查看试题解析
6. 分式方程 $\frac{1}{x - 2} = \frac{3}{x}$ 的解为（）

A、 $x = 4$ B、 $x = 3$ C、 $x = 2$ D、无解

查看试题解析
7. 利用尺规作图，不能作出唯一三角形的是（　　）

A、已知两边及其中一边的对角 B、已知三边 C、已知两边及其夹角 D、已知两角及其夹边

查看试题解析
8. 如图， $A B ∥ C D$ ， $A D ∥ B C$ ， AC和BD相交于点O ，则图中全等三角形共有（）

A、2对 B、3对 C、4对 D、5对

查看试题解析
9. 如图，数轴上表示不等式的解集为（）

A、 $x \geq - 1$ B、 $x > - 1$ C、 $x \leq - 1$ D、 $x < - 1$

查看试题解析
10. 如图，点P是AB上任一点， $∠ A B C = ∠ A B D$ ，从下列各条件中补充一个条件，不一定能推出 $△ A P C ≌ △ A P D$ 的是（）

A、 $B C = B D$ B、 $∠ A C B = ∠ A D B$ C、 $A C = A D$ D、 $∠ C A B = ∠ D A B$

查看试题解析
11. 如图，在△ABC中，AB＝3，AC＝4，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC分别交AB、AC于M、N，则△AMN的周长为（）

A、4 B、6 C、7 D、8

查看试题解析
12. 观察下列计算过程：因为 $1 1^{2} = 121$ ，所以 $\sqrt{121} = 11$ ，因为 $11 1^{2} = 12321$ ，所以 $\sqrt{12321} = 111$ ，因为 $111 1^{2} = 1234321$ ，所以 $\sqrt{1234321} = 111 1^{2}$ …，由此猜想 $\sqrt{12345678987654321} =$ （）

A、111111111 B、11111111 C、1111111 D、111111

查看试题解析

二、填空题（本大题共6小题，每小题2分，共12分.请将答案填在答题卡上）

13. 计算： $\frac{5 x + 3 y}{x^{2} - y^{2}} - \frac{2 x}{x^{2} - y^{2}} =$ .

查看试题解析
14. 在 $\frac{22}{7}$ ， 3.14159， $\sqrt{7}$ ，－8， $\sqrt[3]{2}$ ， 0.6，0， $\sqrt{36}$ ， $\frac{π}{3}$ 中是无理数的个数有个.

查看试题解析
15. 比较大小： $\sqrt{31}$ 6.（填“＞”、“＝”或“＜”）

查看试题解析
16. 将命题“两个全等三角形的周长相等”改写成“如果…那么…”的形式.

查看试题解析
17. 已知C、D两点在线段 $A B$ 的垂直平分线上，且 $∠ A C B = 30 °$ ， $∠ A D B = 70 °$ ，则 $∠ C A D =$ .

查看试题解析
18. 已知关于 $x$ 的不等式 $(2 a - 4) x < 2 a - 4$ 的解集是 $x > 1$ ，则 $a$ 的取值范围为．

查看试题解析

三、解答题（本大题共8小题，共72分.解答应写出文字说明、证明过程或演算步骤）

19. 计算： $\sqrt{{(- 3)}^{2}} - | \sqrt{3} - 2 | + {(- \frac{1}{3})}^{- 2} - {(2019 - π)}^{0}$

查看试题解析
20. 化简：

(1)、 $\frac{a}{a - 1} + \frac{1}{1 - a}$ ；

(2)、 $(a - \frac{1}{a}) \div \frac{a^{2} - 2 a + 1}{a}$ ．

查看试题解析
21. 解不等式： $- \frac{x - 1}{2} + 1 > x$ ，并把解集在数轴上表示出来.

查看试题解析
22. 先化简，再求值： $(\frac{y^{2}}{x + y} - y) \div \frac{x - y}{x^{2} - y^{2}} - (x - 2 y) (x + y)$ ，其中 $x = - 1$ ， $y = 2$ .

查看试题解析
23. 已知：如图，在 $△ A B C$ 中， $A D$ 平分 $∠ B A C .$ 在 $A B$ 上截取 $A E = A C$ ，连结 $D E .$ 若 $B C = 6 c m$ ， $B E = 3 c m$ ．

(1)、求证： $△ A E D$ ≌ $△ A C D$ ；

(2)、求 $△ B E D$ 的周长．

查看试题解析
24. 某汽车站北广场将于2023年底投入使用，计划在广场内种植A、B两种花木共6600棵，若A花木数量是B花木数量的2倍少600棵.

(1)、A、B两种花木的数量分别是多少棵？

(2)、如果园林处安排26人同时种植这两种花木，每人每天能种植A花木60棵或B花木40棵，应分别安排多少人种植A花木和B花木，才能确保同时完成各自的任务.

查看试题解析
25. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ， $E$ 为 $A C$ 边的中点，过点A作 $A D ⊥ A B$ 交 $B E$ 的延长线于点 $D ， C G$ 平分 $∠ A C B$ 交 $B D$ 于点 $G$ ， $F$ 为 $A B$ 边上一点，连接 $C F$ ，且 $∠ A C F = ∠ C B G$ ．求证：

(1)、 $△ A F C$ $≌ △ C G B$ ；

(2)、 $A F = A D$ ．

查看试题解析
26. 【综合与实践】
【问题情境】无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来，比如 $π$ 、 $\sqrt{2}$ 等，而常用“……”或者“≈”的表示方法都不够百分百准确；于是小刚用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分，你同意小刚的表示方法吗？
【猜想证明】事实上，小刚的表示方法是有道理的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分.又例如：因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ，即 $2 < \sqrt{5} < 3$ ，所以， $\sqrt{5}$ 的整数部分为2，小数部分为 $\sqrt{5} - 2$ ，也就是说，任何一个无理数，都可以夹在两个相邻的整数之间.
【问题解决】

(1)、试着写出 $\sqrt{13}$ 的整数部分和小数部分；

(2)、 $10 + \sqrt{7}$ 也是夹在两个整数之间的，可以表示为 $a < 10 + \sqrt{7} < b$ ，则 $a + b$ 的值是多少？

(3)、若 $\sqrt{40} - 4 = x + y$ ，其中x是整数，且 $0 < y < 1$ .求： $x - y$ 的相反数.

查看试题解析