广西壮族自治区柳州市鹿寨县2023-2024学年八年级上学期1月期末数学试题
试卷更新日期:2024-03-15 类型:期末考试
一、单选题(共12小题,每小题3分,共36分)
-
1. 以下四家银行的标志图中,不是轴对称图形的是 ( )A、
 B、
B、 C、
C、 D、
D、 2. 年月日,“芯科技,创未来”中国汽车芯片高峰论坛在中国电科智能科技园举行.中国电科协同相关企业,发布了 , , 等数十款汽车电子产品,发布的车规级高安全芯片,采用()国产工艺,可应用于汽车疲劳驾驶预警、车载信息娱乐等领域.将数据“”转换成米用科学记数法表示为( )
2. 年月日,“芯科技,创未来”中国汽车芯片高峰论坛在中国电科智能科技园举行.中国电科协同相关企业,发布了 , , 等数十款汽车电子产品,发布的车规级高安全芯片,采用()国产工艺,可应用于汽车疲劳驾驶预警、车载信息娱乐等领域.将数据“”转换成米用科学记数法表示为( ) A、 B、 C、 D、3. 下列图形中AD是三角形ABC的高线的是( )A、
A、 B、 C、 D、3. 下列图形中AD是三角形ABC的高线的是( )A、 B、
B、 C、
C、 D、
D、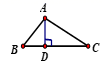 4. 下列计算正确的是( )A、a2+a3=a5 B、a3•a3=a9 C、(a3)2=a6 D、(ab)2=ab25. 若长度为x,2,3的三条线段能组成一个三角形,则x的值可能为( )A、6 B、5 C、1 D、36. 等腰三角形的一个角是70°,它的底角的大小为( )A、70° B、40° C、70°或40° D、70°或55°7. 把代数式中的x,y同时扩大2倍后,代数式的值( )A、扩大为原来的1倍 B、扩大为原来2倍 C、扩大为原来的4倍 D、缩小为原来的一半8. 下列计算正确的是( )A、 B、 C、 D、9. 若是完全平方式,则m的值等于( )A、1或5 B、5 C、7 D、7或10. 买一个足球需元,买一个篮球需元,则买5个足球和4个篮球共需( )A、元 B、元 C、元 D、元11. 如图,将△ABC绕点C顺时针旋转35°,得△A′B′C,若AC⊥A′B′,则∠BAC=( )
4. 下列计算正确的是( )A、a2+a3=a5 B、a3•a3=a9 C、(a3)2=a6 D、(ab)2=ab25. 若长度为x,2,3的三条线段能组成一个三角形,则x的值可能为( )A、6 B、5 C、1 D、36. 等腰三角形的一个角是70°,它的底角的大小为( )A、70° B、40° C、70°或40° D、70°或55°7. 把代数式中的x,y同时扩大2倍后,代数式的值( )A、扩大为原来的1倍 B、扩大为原来2倍 C、扩大为原来的4倍 D、缩小为原来的一半8. 下列计算正确的是( )A、 B、 C、 D、9. 若是完全平方式,则m的值等于( )A、1或5 B、5 C、7 D、7或10. 买一个足球需元,买一个篮球需元,则买5个足球和4个篮球共需( )A、元 B、元 C、元 D、元11. 如图,将△ABC绕点C顺时针旋转35°,得△A′B′C,若AC⊥A′B′,则∠BAC=( )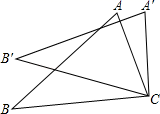 A、65° B、75° C、55° D、35°12. 如图,在中,、分别是、边上的高,在上截取 , 在的延长线上截取 , 连接、 , 则下列结论错误的是( )
A、65° B、75° C、55° D、35°12. 如图,在中,、分别是、边上的高,在上截取 , 在的延长线上截取 , 连接、 , 则下列结论错误的是( ) A、 B、 C、为等腰直角三角形 D、
A、 B、 C、为等腰直角三角形 D、二、填空题(共6小题,每小题2分,共12分)
-
13. 要使分式有意义,则x的取值范围为 .14. 师傅在做完门框后,为防止门框变形,常常需钉两根斜拉的木条,这样做的数学原理是 .15. 分解因式:.16. 如图,的度数是.
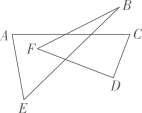 17. 若三角形的三边满足 , 则此三角形的形状是 .18. 如图,在中, , 以为边向上作正方形 , 以为边作正方形 , 点D落在上,连接 , . 若 , , 则的面积为 .
17. 若三角形的三边满足 , 则此三角形的形状是 .18. 如图,在中, , 以为边向上作正方形 , 以为边作正方形 , 点D落在上,连接 , . 若 , , 则的面积为 .
三、解答题(共7小题,72分)
-
19. 计算:20. 已知 , 求代数式的值.21. 如图,三个顶点的坐标分别为 .
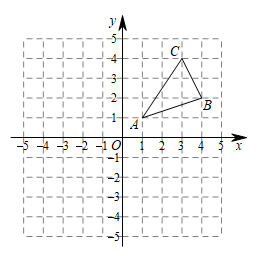 (1)、请写出关于轴对称的的各顶点坐标;(2)、请画出关于轴对称的;(3)、在轴上求作一点 , 使点到两点的距离和最小,请标出点,并直接写出点的坐标 .22. 疫情期间,学校开通了教育互联网在线学习平台.为了解学生使用电子设备种类的情况,小淇设计了调查问卷,对该校七(1)班和七(2)班全体同学进行了问卷调查,发现使用了三种设备:A(平板)、B(电脑)、C(手机),根据调查结果绘制成如下两幅不完整的统计图.请根据图中信息解答下列问题.
(1)、请写出关于轴对称的的各顶点坐标;(2)、请画出关于轴对称的;(3)、在轴上求作一点 , 使点到两点的距离和最小,请标出点,并直接写出点的坐标 .22. 疫情期间,学校开通了教育互联网在线学习平台.为了解学生使用电子设备种类的情况,小淇设计了调查问卷,对该校七(1)班和七(2)班全体同学进行了问卷调查,发现使用了三种设备:A(平板)、B(电脑)、C(手机),根据调查结果绘制成如下两幅不完整的统计图.请根据图中信息解答下列问题.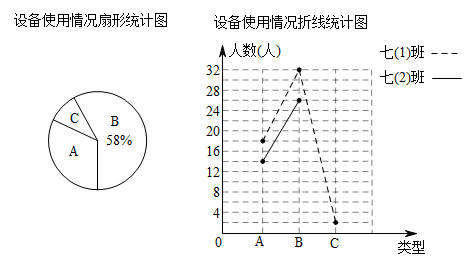 (1)、此次被调查的学生总人数为;(2)、求扇形统计图中代表类型C的扇形的圆心角,并补全折线图;(3)、若该校七年级学生共有1000人,试根据此次调查结果,估计该校七年级学生中类型C学生约有多少人.23. 如图, , , , , 垂足分别是D,E,BE=0.8,DE=1.7,求AD的长.
(1)、此次被调查的学生总人数为;(2)、求扇形统计图中代表类型C的扇形的圆心角,并补全折线图;(3)、若该校七年级学生共有1000人,试根据此次调查结果,估计该校七年级学生中类型C学生约有多少人.23. 如图, , , , , 垂足分别是D,E,BE=0.8,DE=1.7,求AD的长.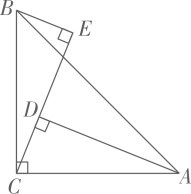 24. 永州市万达广场筹建之初的一项挖土工程招标时,接到甲、乙两个工程队的投标书,每施工一天,需付甲工程队工程款2.4万元,付乙工程队工程款1.8万元,工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:
24. 永州市万达广场筹建之初的一项挖土工程招标时,接到甲、乙两个工程队的投标书,每施工一天,需付甲工程队工程款2.4万元,付乙工程队工程款1.8万元,工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:(方案一)甲队单独完成这项工程,刚好按规定工期完成;
(方案二)乙队单独完成这项工程要比规定工期多用6天;
(方案三)若由甲、乙两队合作做5天,剩下的工程由乙队单独做,也正好按规定工期完工.
(1)、请你求出完成这项工程的规定时间;(2)、如果你是工程领导小组的组长,为了节省工程款,同时又能如期完工,你将选择哪一种方案?说明理由.