广东省珠海市斗门区2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-03-15 类型:期末考试
一、选择题(本大题10小题,每小题3分,共30分)
-
1. 下列各组中的三条线段不能组成三角形的是( )A、1,1,1 B、1,2,3 C、2,3,4 D、2,2,12. 在平面直角坐标系中,点关于轴对称的点是( )A、 B、 C、 D、3. 如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
 A、120° B、90° C、100° D、30°4. 要使分式有意义,x应满足的条件是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 与的边重合, . 添加下一个条件后,仍无法判定的是( )
A、120° B、90° C、100° D、30°4. 要使分式有意义,x应满足的条件是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 与的边重合, . 添加下一个条件后,仍无法判定的是( ) A、 B、 C、 D、7. 下面四个图形中,线段不是的高的是( )A、
A、 B、 C、 D、7. 下面四个图形中,线段不是的高的是( )A、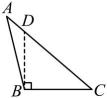 B、
B、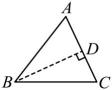 C、
C、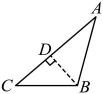 D、
D、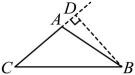 8. 下列式子的化简结果为的是( )A、 B、 C、 D、9. 如图,在中,于D , , 则( )
8. 下列式子的化简结果为的是( )A、 B、 C、 D、9. 如图,在中,于D , , 则( ) A、2 B、3 C、2.5 D、1.510. 如图,中, , , 要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形,其作法错误的是( )A、
A、2 B、3 C、2.5 D、1.510. 如图,中, , , 要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形,其作法错误的是( )A、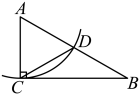 B、
B、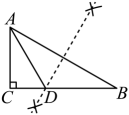 C、
C、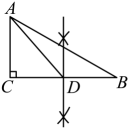 D、
D、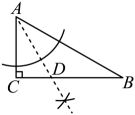
二、填空题(本大题5小题,每小题3分,共15分)
-
11. 计算:.12. 对分式和进行通分,它们的最简公分母为 .13. 已知正n边形的一个外角是45°,则n=14. 如图,在中,的角平分线交于点 , 则的面积是 .
 15. 如图,在等腰三角形中, , D为延长线上一点,且 , 垂足为C , 连接 , 若 , 则的面积为 .
15. 如图,在等腰三角形中, , D为延长线上一点,且 , 垂足为C , 连接 , 若 , 则的面积为 .
三、解答题(一)(本大题4小题,每小题6分,共24分)
-
16. 分解因式:x2y-4y= .17. 先化简,再求值: , 其中 .18. 如图,点B、C、E、F共线,AB=DC , ∠B=∠C , BF=CE .
求证:△ABE≌△DCF .
 19. 如图,在四边形ABCD中,BP,CP分别平分∠ABC和∠BCD,若∠A=90°,∠D=130°,求∠P的度数.
19. 如图,在四边形ABCD中,BP,CP分别平分∠ABC和∠BCD,若∠A=90°,∠D=130°,求∠P的度数.
四、解答题(二)(本大题3小题,每小题9分,共27分)
-
20. 一项工程,甲、乙两公司合做,12天可以完成,如果甲乙公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍.(1)、甲、乙公司单独完成此项工程,各需多少天?(2)、若已知甲乙合做完成此项工程共需费用102000元,并且乙公司每天费用比甲公司每天费用少1500元,分别计算甲、乙单独完成此项工程各需多少费用并选择合理的施工方案.21. 在等边中,点为边上任意一点,点在边的延长线上,且 .
 (1)、如图1,若点为的中点,求证:;(2)、如图2,若点为上任意一点,求证: .22. 小戴同学通过计算下列两位数的乘积,发现结果也存在一定的规律,请你补充小戴同学的探究过程:
(1)、如图1,若点为的中点,求证:;(2)、如图2,若点为上任意一点,求证: .22. 小戴同学通过计算下列两位数的乘积,发现结果也存在一定的规律,请你补充小戴同学的探究过程:, , ,
(1)、利用发现的规律计算 .(2)、根据发现,若设一个两位数的十位上的数字为 , 个位上的数字为 , 则另一个两位数的个位上的数字为;用含、的等式表示以上两位数相乘的规律;
(3)、请用所学知识证明②中的规律.五、解答题(三)(本大题2小题,每小题12分,共24分)
-
23. 在中, , , 为边延长线上一点,连接 .
 (1)、如图1,当时,求证:;(2)、如图2,当时,求证:;、(3)、如图3,当时,求证: .24. 通过完全平方公式的灵活运用,可以解决很多数学问题.
(1)、如图1,当时,求证:;(2)、如图2,当时,求证:;、(3)、如图3,当时,求证: .24. 通过完全平方公式的灵活运用,可以解决很多数学问题.例如:若 , , 求的值.
解: , ,
, .
,
.
根据上面的解题思路与方法解决下列问题:
(1)、若 , , 则;(2)、已知 , 分别以、为直角边向两侧作等腰直角和等腰直角 , 其中 .①如图1,若 , 的面积为 , 和的面积之和为26,求线段的长;

②如图2,若与在同一直线上,连接 , 延长与交于点 , 连接并延长与边交于点 , 且 , 若和的面积之和为20,的面积为6,求线段的长.
