广东省惠州市惠阳区2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-03-15 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，满分30分）

1. $- \frac{3}{2}$ 的倒数是（）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、 $- \frac{3}{2}$ D、 $- \frac{2}{3}$

查看试题解析
2. 科学家发现，距离银河系2500000光年之遥的仙女星系正在向银河系靠近．其中2500000用科学记数法表示为（）

A、 $0.25 \times 10^{7}$ B、 $2.5 \times 10^{6}$ C、 $2.5 \times 10^{7}$ D、 $25 \times 10^{5}$

查看试题解析
3. 第19届亚运会将于2023年9月23日至2023年10月8日在杭州举行，中国代表队自1982年新德里亚运会以来，连续蝉联金牌榜第一，中国已经成为亚洲体育第一强国．小明将“亚、洲、体、育、第、一”这六个汉字分别写在某正方体的表面上，如图是它的一种展开图，现在原正方体中，与“一”字所在面相对的面上的汉字是（　　）

A、亚 B、洲 C、体 D、育

查看试题解析
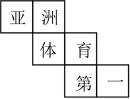4. 已知 $(1 - n) x^{| 2 n | - 1} + 9 = 0$ 是关于 $x$ 的一元一次方程，则 $n$ 的值为（）

A、 $1$ B、 $- 1$ C、 $0$ D、 $1$ 或 $- 1$

查看试题解析
5. 某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分（如图），发现剩下的银杏叶的周长比原银本叶的周长要小，能正确解释这一现象的数学知识是（　　）

A、两点确定一条直线 B、点动成线 C、直线是向两方无限延伸的 D、两点之间线段最短

查看试题解析
6. 下列单项式中，系数最小的是（）

A、 $- a x^{3}$ B、 $- π x y^{2}$ C、 $- 3 a b c^{3}$ D、 $\frac{1}{3} x y^{2}$

查看试题解析
7. 把多项式 $- 3 x^{2} - 2 x + y - x y + y^{2}$ 一次项结合起来，放在前面带有“+”号的括号里，二次项结合起来，放在前面带有“-”号的括号里，等于（）

A、 $(- 2 x + y - x y) - (3 x^{2} - y^{2})$ B、 $(2 x + y) - (3 x^{2} - x y + y^{2})$ C、 $(- 2 x + y) - (- 3 x^{2} - x y + y^{2})$ D、 $(- 2 x + y) - (3 x^{2} + x y - y^{2})$

查看试题解析
8. 如图，射线 $O A$ 表示北偏东 $30 °$ 方向，射线 $O B$ 表示北偏西 $50 °$ 方向，点C在射线 $O B$ 的反向延长线上，则 $∠ A O C$ 的度数为（）

A、 $100 °$ B、 $90 °$ C、 $80 °$ D、 $60 °$

查看试题解析
9. 我国古代对于利用方程解决实际问题早有研究，《九章算术》中提到一道“以绳测井”的题：“以绳测井，若将绳三折测之，绳多四尺；若将绳四折测之，绳多一尺．绳长、井深各几何？”这道题大致意思是：用绳子测量水井深度，如果将绳子折成三等份，那么每等份井外余绳四尺：如果将绳子折成四等份，那么每等份井外余绳一尺．问绳长和井深各多少尺？若设井深为x尺，则下列求解井深的方程正确的是（）

A、 $3 (x + 4) = 4 (x + 1)$ B、 $3 x + 4 = 4 x + 1$ C、 $\frac{1}{3} x + 4 = \frac{1}{4} x + 1$ D、 $\frac{1}{3} x - 4 = \frac{1}{4} x - 1$

查看试题解析
10. 找出以下图形变化的规律，则第101个图形中黑色正方形的数量是（）

A、149 B、150 C、151 D、152

查看试题解析

二、填空题（本题共6题，每小题3分，共18分）

11. 已知 $x = 2$ 是关于x的一元一次方程 $m x + 2 = 0$ 的解，则m的值为．

查看试题解析
12. 如果一个角的度数为 $43 ° 3 6^{'}$ ，那么这个角的补角的度数为．

查看试题解析
13. 多项式 $- 3 a b^{2} - a b - 2 a^{2} b^{2} + 1$ 的次数是．

查看试题解析
14. 我国南北朝时期著名的数学家和天文学家祖冲之最先将圆周率的计算准确到了小数点后七位，比国外的科学家早了1000多年．祖冲之推演出圆周率在3.1415926到3.1415927之间，若圆周率取近似值，精确到千分位，则约为．

查看试题解析
15. 甲、乙两个工程队共同承接了某村“煤改气”工程，甲队单独施工需10天完成，乙队单独施工需15天完成．若甲队先做5天，剩下部分由两队合做，则完成该工程还需要天．

查看试题解析
16. 如图，有 $12$ 个方格，每个方格内都有一个数，若任何相邻三个数的和都是 $18$ ，则x的值是．
5
A
B
C
D
E
F
x
G
H
P
$10$

查看试题解析

三、解答题（一）（本题共3小题，每题7分，共21分）

17. 计算： $| - 2 - 4 | - 32 \div {(- 2)}^{3} \times (- \frac{1}{4})$

查看试题解析
18. 某教辅书中一道整式运算的参考答案污损看不清了，形式如下：
解：原式＝█ $+ 2 (3 y^{2} - 2 x)$
$= - 11 x + 8 y$ ．

(1)、求污损部分的整式；

(2)、当x＝2，y＝﹣3时，求污损部分整式的值．

查看试题解析
19. 我们将 $| \begin{array}{l} a & b \\ c & d \end{array} |$ 这样的式子称为二阶行列式，它的运算法则公式表示就是 $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ ．若二阶行列式 $| \begin{array}{l} 2 x - 3 & \frac{1}{3} \\ x + 2 & \frac{1}{4} \end{array} |$ 的值为1，请写出求x的具体过程．

查看试题解析

四、解答题（二）（本题共3小题，每小题9分，共27分）

20. 某校组织学生参加2022年冬奥知识问答，问答活动共设有20道选择题，每题必答，每答对一道题加分，答错一道题减分，下表中记录了A、B、C三名学生的得分情况：
参赛学生
答对题数
答错题数
得分
A
20
0
100
B
18
2
86
C
15
5
65
请结合表中所给数据，回答下列问题：

(1)、本次知识问答中，每答对一题加分，每答错一题减分；

(2)、若小刚同学参加了本次知识问答，下列四个选项中，那一个可能是小刚的得分： ▲ （填写选项）；
A.75；B.63；C.56；D.44
并请你计算他答对了几道题，写出解答过程，（列方程解决问题）

查看试题解析
21. 一般情况下 $\frac{a}{2} + \frac{b}{3} = \frac{a + b}{2 + 3}$ 不成立，但有些数可以使得它成立，例如a=b=0．我们称使得 $\frac{a}{2} + \frac{b}{3} = \frac{a + b}{2 + 3}$ 成立的一对数a，b为“相伴数对”，记为（a，b）．

(1)、若（1，b）是“相伴数对”，求b的值.

(2)、若（m，n）是“相伴数对”，求整式26m+4n-2（4m-2n）+5的值．

查看试题解析
22. 已知O是直线 $A B$ 上一点， $∠ C O D$ 是直角， $O E$ 平分 $∠ B O C$ ．

(1)、【初步尝试】如图（1），若 $∠ A O C = 30 °$ ，则 $∠ D O E$ 的度数＝；

(2)、【类比探究】在图（1）中，若 $∠ A O C = α$ ，求 $∠ D O E$ 度数；

(3)、【拓展运用】如图（2）的位置关系，探究 $∠ A O C$ 与 $∠ D O E$ 之间的数量关系，直接写出你的结论．

查看试题解析

五、解答题（三）（本题共2题，每题12分，共24分）

23. 观察下列图形及图形所对应的等式，探究图形阴影部分的面积变化与对应等式的规律，并解答下列问题：
① $2^{2} - 1^{2} = 2 \times 1 + 1 \times 1$ ；
② $3^{2} - 2^{2} = 3 \times 1 + 2 \times 1$ ；
③ $4^{2} - 3^{2} = 4 \times 1 + 3 \times 1$ ；
④ $5^{2} - 4^{2} =$ ____；
……

(1)、补全第四个等式，并直接写出第n个图对应的等式： ▲ ．

(2)、计算： $1^{2} - 2^{2} + 3^{2} - 4^{2} + 5^{2} - 6^{2} + ⋯ + 9 9^{2} - 10 0^{2}$ ．

(3)、若x是正整数，且 ${(3 x + 2)}^{2} - 2025 = {(3 x + 1)}^{2}$ ，求x的值．

查看试题解析
24. 已知：b是最小的正整数，且a、b满足 ${(c - 5)}^{2} + | a + b | = 0$ ．

(1)、请求出a、b、c的值；

(2)、数轴上点A、B、C对应的数分别是a、b、c ，点P为数轴上的一个动点，其对应的数为x ，若满足 $P C = 2 P A$ ，求x的值．

(3)、在（1）、（2）的条件下，点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动，假设t秒钟过后，若点B与点C之间的距离表示为 $B C$ ，点A与点B之间的距离表示为 $A B$ ．请问： $B C - A B$ 的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．

查看试题解析

参赛学生	答对题数	答错题数	得分
A	20	0	100
B	18	2	86
C	15	5	65