广东省梅州市梅县区2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-03-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各选项中，是无理数的是（）

A、 $\frac{5}{7}$ B、2023 C、 $- \sqrt{9}$ D、 $\sqrt{8}$

查看试题解析
2. 下列各组数分别为一个三角形三边的长，其中能构成直角三角形的一组是（）

A、1，2，3 B、2，3，4 C、3，4，5 D、4，5，6

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $3 \sqrt{2} - \sqrt{2} = 3$ C、 $\sqrt{18} \div 3 = \sqrt{6}$ D、 $\sqrt{8} = 2 \sqrt{2}$

查看试题解析
4. 袁隆平院士是中国杂交水稻育种专家，被誉为“世界杂交水稻之父”，某村引进了袁隆平水稻研究所的甲、乙两种水稻良种，各选6块条件相同的试验田，同时播种并核定亩产，结果甲、乙两种水稻的平均产量均约为 $800 k g$ /亩，方差分别为 $S_{甲}^{2} = 141.7$ ， $S_{乙}^{2} = 433.3$ ，则产量稳定、更适合推广的品种为（）

A、甲 B、乙 C、甲、乙均可 D、无法确定

查看试题解析
5. 关于x、y的二元一次方程 $2 x + y = 7$ 的自然数解有（）

A、3组 B、4组 C、5组 D、6组

查看试题解析
6. 如图，长方形 $A B C D$ 中， $A B = 3 c m$ ， $A D = 9 c m$ ，将此长方形折叠，使点D与点B重合，折痕为 $E F$ ，则 $△ A B E$ 的面积为（）

A、 $6 c m^{2}$ B、 $8 c m^{2}$ C、 $10 c m^{2}$ D、 $12 c m^{2}$

查看试题解析
7. 下列关于一次函数 $y = - x + 1$ 的说法中，错误的是（）

A、其图象经过第一、二、四象限 B、其图象与 $x$ 轴的交点坐标为 $(- 1 ， 0)$ C、其图象一定经过点 $(2 ， - 1)$ D、 $y$ 随 $x$ 的增大而减小

查看试题解析
8. 如图，将一副直角三角板按图中所示的位置摆放，两条斜边互相平行，则∠1=（　　）

A、 $7 5^{∘}$ B、 $7 0^{∘}$ C、 $6 5^{∘}$ D、 $6 0^{∘}$

查看试题解析
9. 在学习完“垃圾分类”的相关知识后，小明和小丽一起收集了一些废电池，小明说：“我比你多收集了7节废电池啊！”小丽说：“如果你给我8节废电池，我的废电池数量就是你的2倍”．如果他们说的都是真的，设小明收集了x节废电池，小丽收集了y节废电池，则可列方程组为（）

A、 ${\begin{array}{l} x - y = 7 \\ x - 8 = 2 (y + 8) \end{array}$ B、 ${\begin{array}{l} x - y = 7 \\ 2 (x - 8) = y + 8 \end{array}$ C、 ${\begin{array}{l} x - y = 7 \\ 2 (x - 8) = y \end{array}$ D、 ${\begin{array}{l} y - x = 7 \\ x + 8 = 2 (y - 8) \end{array}$

查看试题解析
10. 如图，在平面直角坐标系上有点 $A (1 ， 0)$ ，点A第一次跳动至点 $A_{1} (- 1 ， 1)$ ，第二次向右跳动3个单位至点 $A_{2} (2 ， 1)$ ，第三次跳动至点 $A_{3} (- 2 ， 2)$ ，第四次向右跳动5个单位至点 $A_{4} (3 ， 2)$ ， …，依此规律跳动下去，点 $A$ 第2023次跳动至 $A_{2023}$ 的坐标是（）

A、 $(1012 ， 1011)$ B、 $(- 1012 ， 1012)$ C、 $(- 1011 ， 1011)$ D、 $(- 1010 ， 1010)$

查看试题解析

二、填空题

11. 比较大小： $\sqrt{17} - 1$ 4（填“＞”、“＜”或“＝”）．

查看试题解析
12. 在平面直角坐标系 $x o y$ 中，点 $A (- 3 ， 4)$ 和点 $B (3 ， 4)$ 关于轴对称．

查看试题解析
13. 命题“三角形的三个内角中至少有两个锐角”是（填“真命题”或“假命题”）．

查看试题解析
14. 已知一次函数 $y = k x + b$ 与 $y = x + 2$ 的图像相交于点 $P (m ， 4)$ ，则关于x ， y的二元一次方程组 ${\begin{array}{l} k x - y = - b \\ y - x = 2 \end{array}$ 的解是.

查看试题解析
15. 如图，在 $△ A B C$ 中， $A D$ 是 $∠ B A C$ 的平分线，过点 $C$ 的射线 $C E$ 与 $A D$ 平行，若 $∠ B = 60 °$ ， $∠ A C B = 30 °$ ，则 $∠ A C E =$ ．

查看试题解析
16. 一个装有进水管和出水管的容器，开始时，先打开进水管注水，3分钟时，再打开出水管排水，8分钟时，关闭进水管，直至容器中的水全部排完.在整个过程中，容器中的水量y（升）与时间x（分钟）之间的函数关系如图所示，则图中a的值为.

查看试题解析

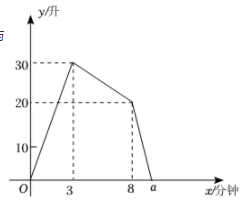
三、解答题

17. 计算： $\sqrt{25} + | 1 - \sqrt{2} | + \sqrt[3]{- 8} - {(- 1)}^{2023}$ ．

查看试题解析
18. 已知关于x ， y的二元一次方程组 ${\begin{array}{l} 2 x + 5 y = 2 \\ 5 x + 2 y = 12 \end{array}$ 的解满足 $x - y = m - 1$ ，求m的值．

查看试题解析
19. 如图：已知，∠HCO＝∠EBC ， ∠BHC+∠BEF＝180°．

(1)、求证：EF $∥$ BH；

(2)、若BH平分∠EBO ， EF⊥AO于F ， ∠HCO＝64°，求∠CHO的度数．

查看试题解析
20. 在平面直角坐标系中， $△ A B C$ 的位置如图所示，已知点 $A$ 的坐标是 $(- 4 ， 3)$

(1)、点 $B$ 的坐标为（，），点 $C$ 的坐标为（，）

(2)、求 $△ A B C$ 的面积．

(3)、作点 $C$ 关于 $y$ 轴的对称点 $C^{'}$ ，那么 $A 、 C^{'}$ 两点之间的距离是．

查看试题解析
21. 李明在某商场购买甲乙两种商品若干次（每次甲，乙两种商品都购买），其中前两次按标价购买，第三次购买时，甲，乙两种商品同时打折，三次购买甲，乙两种商品的数量和费用情况如表所示：

购买甲商品的数量
购买乙商品的数量
购买总费用
第一次
5
5
900
第二次
6
7
1180
第三次
9
8
1064

(1)、求甲、乙两种商品的标价各是多少元？

(2)、若李明第三次购买时，甲、乙两种商品的折扣相同，则商场是打几折出售这两种商品的？

查看试题解析
22. 为推进乡村振兴，把家乡建设成为生态宜居、交通便利的美丽家园，某地大力修建崭新的公路．如图，现从A地分别向C、D、B三地修了三条笔直的公路 $A C$ 、 $A D$ 和 $A B$ ， C地、D地、B地在同一笔直公路上，公路 $A C$ 和公路 $C B$ 互相垂直，又从D地修了一条笔直的公路 $D H$ 与公路 $A B$ 在H处连接，且公路 $D H$ 和公路 $A B$ 互相垂直，已知 $A C = 9$ 千米， $A B = 15$ 千米， $B D = 5$ 千米．

(1)、求公路 $C D$ 、 $A D$ 的长度；

(2)、若修公路 $D H$ 每千米的费用是2000万元，请求出修建公路 $D H$ 的费用．

查看试题解析
23. 新颁布的《义务教育课程方案和课程标准（2022年版）》优化了课程设置，将劳动从综合实践活动课程中独立出来，彰显劳动教育的重要性．为了解某校学生一周内劳动教育情况，随机抽查部分学生一周内课外劳动时间，将数据进行整理并制成如下统计图的图1和图2．

请根据图中提供的信息，解答下面的问题：

(1)、求图1中m的值为，此次抽查数据的中位数是 h；

(2)、求该校此次抽查的学生一周内平均课外劳动时间；

(3)、若该校共有2000名学生，请你估计该校学生一周内课外劳动时间不小于 $3 h$ 的人数．

查看试题解析
24. 共享电动车是一种新理念下的交通工具：主要面向 $3 ∼ 10 k m$ 的出行市场，现有 $A$ 、 $B$ 两种品牌的共享电动车，收费与骑行时间之间的函数关系如图所示，其中 $A$ 品牌收费方式对应 $y_{1}$ ， $B$ 品牌的收费方式对应 $y_{2}$ .

(1)、 $B$ 品牌10分钟后，每分钟收费；

(2)、求出 $A$ 品牌的函数关系式；

(3)、求两种收费相差1.4元时， $x$ 的值.

查看试题解析
25. 如图，在平面直角坐标系中，直线 $l_{1} ： y = \frac{3}{4} x$ 与直线 $l_{2} ： y = k x + b (k \neq 0)$ 相交于点 $A (a ， 3)$ ，直线 $l_{2}$ 与y轴交于点 $B (0 ， - 5)$ .

(1)、求直线 $l_{2}$ 的函数解析式；

(2)、将 $△ O A B$ 沿直线 $l_{2}$ 翻折得到 $△ C A B$ ，使点O与点C重合， $A C$ 与x轴交于点D.求证： $A C ∥ O B$ ；

(3)、在直线 $B C$ 下方是否存在点P，使 $△ B C P$ 为等腰直角三角形？若存在，直接写出点P坐标；若不存在，请说明理由.

查看试题解析

	购买甲商品的数量	购买乙商品的数量	购买总费用
第一次	5	5	900
第二次	6	7	1180
第三次	9	8	1064