广东省惠州市2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-03-15 类型:期末考试
一、选择题(本题共10小题,每小题3分,共30分)
-
1. 下列四个字中可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三条线段,能组成三角形的是( )A、1,3,4 B、2,2,7 C、4,5,7 D、3,3,63. 下列汽车标志中,不是由多个全等图形组成的是( )A、
2. 下列长度的三条线段,能组成三角形的是( )A、1,3,4 B、2,2,7 C、4,5,7 D、3,3,63. 下列汽车标志中,不是由多个全等图形组成的是( )A、 B、
B、 C、
C、 D、
D、 4. 计算的结果是( )A、A B、 C、 D、5. 在平面直角坐标系中,若点P的坐标为 , 则点P关于y轴对称的点的坐标为( )A、 B、 C、 D、6. 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )A、
4. 计算的结果是( )A、A B、 C、 D、5. 在平面直角坐标系中,若点P的坐标为 , 则点P关于y轴对称的点的坐标为( )A、 B、 C、 D、6. 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )A、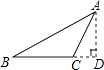 B、
B、 C、
C、 D、
D、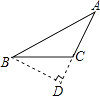 7. 下列式子中是分式的是( )A、 B、 C、 D、8. 如图,小虎用10块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板 , 点C在上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离的长度为( )
7. 下列式子中是分式的是( )A、 B、 C、 D、8. 如图,小虎用10块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板 , 点C在上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离的长度为( )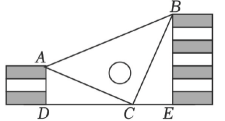 A、 B、 C、 D、9. 如图,若 , , 则等于( )
A、 B、 C、 D、9. 如图,若 , , 则等于( ) A、 B、 C、 D、10. 小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).A、
A、 B、 C、 D、10. 小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).A、 B、
B、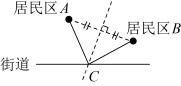 C、
C、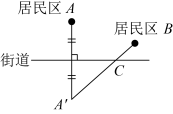 D、
D、
二、填空题(本题共5小题,每小题3分,共15分)
-
11. 分解因式: = .12. 若代数式有意义,则实数x的取值范围是 .13. 在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1=°
 14. 如图,在中, , 以顶点A为圆心,适当长为半径画弧,分别交于点M , N , 再分别以点M,N为圆心,大于的长为半径画弧,两弧交于点P , 作射线交边于点D , 若 , 则的面积是 .
14. 如图,在中, , 以顶点A为圆心,适当长为半径画弧,分别交于点M , N , 再分别以点M,N为圆心,大于的长为半径画弧,两弧交于点P , 作射线交边于点D , 若 , 则的面积是 . 15. 如图,在中, , , 线段的垂直平分线分别交于点D、E , 连接 . 若 , 则的长为 .
15. 如图,在中, , , 线段的垂直平分线分别交于点D、E , 连接 . 若 , 则的长为 .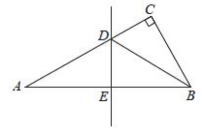
三、解答题(一)(本题共3小题,每小题8分,共24分)
-
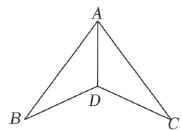
16.(1)、分式化简:(2)、如图, .
求证: .
 17. 将一个正六边形的纸片对折,并完全重合.那么得到的图形是几边形?它的内角和(按一层计算)是多少度?18. 随着中国网民规模突破亿、博物馆美育不断向线上拓展.敦煌研究院顺势推出数字敦煌文化大使伽瑶 , 受到广大敦煌文化爱好者的好评.某工厂计划制作个伽瑶玩偶摆件,为了尽快完成任务,实际平均每天完成的数量是原计划的倍,结果提前天完成任务.问原计划平均每天制作多少个摆件?
17. 将一个正六边形的纸片对折,并完全重合.那么得到的图形是几边形?它的内角和(按一层计算)是多少度?18. 随着中国网民规模突破亿、博物馆美育不断向线上拓展.敦煌研究院顺势推出数字敦煌文化大使伽瑶 , 受到广大敦煌文化爱好者的好评.某工厂计划制作个伽瑶玩偶摆件,为了尽快完成任务,实际平均每天完成的数量是原计划的倍,结果提前天完成任务.问原计划平均每天制作多少个摆件?
四、解答题(二)(本题共3小题,每小题9分,共27分)
-
19. 回答下列问题:(1)、计算:①;② .
③;④ .
(2)、总结公式(3)、已知a,b,m均为整数,且 . 求m的所有可能值.20. 如图,在由边长为1个单位长度的小正方形组成的网格中,点均为格点(网格线的交点). (1)、画出线段关于直线对称的线段;(2)、将线段向左平移2个单位长度,再向上平移1个单位长度,得到线段 , 画出线段;(3)、描出线段上的点及直线上的点 , 使得直线垂直平分 .21. 如图, BD 是 △ABC的角平分线, DE∥BC ,交 AB 于点E.
(1)、画出线段关于直线对称的线段;(2)、将线段向左平移2个单位长度,再向上平移1个单位长度,得到线段 , 画出线段;(3)、描出线段上的点及直线上的点 , 使得直线垂直平分 .21. 如图, BD 是 △ABC的角平分线, DE∥BC ,交 AB 于点E.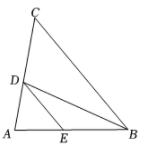 (1)、求证: .(2)、当AB=AC时,请判断 CD 与ED的大小关系,并说明理由.
(1)、求证: .(2)、当AB=AC时,请判断 CD 与ED的大小关系,并说明理由.五、解答题(三)(本题共2小题,每小题12分,共24分)
-
22.

图① 图② 图③
(1)、观察图①,用等式表示图中图形的面积的运算为 .【类比探究】观察图②,用等式表示图中阴影部分图形的面积和为 .
【应用】根据图②所得的公式,若 , 则 .
(2)、若x满足 , 求的值.【拓展】如图③,某学校有一块梯形空地于点 . 该校计划在和区域内种花,在和的区域内种草.经测量种花区域的面积和为 , , 直接写出种草区域的面积和.
23. 如图,在中,于于相交于点O , 且 .
(备用图1) (备用图2)
(1)、求°.(2)、试说明:;(3)、点F是直线上的一点且 , 动点P从点O出发,沿线段以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动.设点P的运动时间为t秒,问是否存在t值,使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等?若存在,请在备用图中画出大致示意图,并求出符合条件的t值;若不存在,请说明理由.