广东省汕头市重点中学2023-2024学年八年级下学期寒假学习质量评估数学试题
试卷更新日期:2024-03-15 类型:开学考试
一、选择题(本大题10小题,每小题3分,共30分)
-
1. 下列冰雪运动项目的图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若分式有意义,则x的取值范围是( )A、x≠-2 B、x≠3 C、x >3 D、x <33. 内角和为1800°的多边形的边数是( )A、12 B、10 C、14 D、154. 在下列运算中,正确的是( )A、x8÷x3= x5 B、(3x)2=6x2 C、x2·x3= x6 D、(x3)2= x55. 若一个三角形的两边长分别为3cm、5cm,则它的第三边的长可能是( )A、1cm B、2cm C、6cm D、8cm6. 华为麒麟990芯片采用了最新的0.000000007米的工艺制程,0.000000007用科学记数法表示为( )A、7×10-9 B、7×10-8 C、0.7×10-9 D、0.7×10-87. 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
2. 若分式有意义,则x的取值范围是( )A、x≠-2 B、x≠3 C、x >3 D、x <33. 内角和为1800°的多边形的边数是( )A、12 B、10 C、14 D、154. 在下列运算中,正确的是( )A、x8÷x3= x5 B、(3x)2=6x2 C、x2·x3= x6 D、(x3)2= x55. 若一个三角形的两边长分别为3cm、5cm,则它的第三边的长可能是( )A、1cm B、2cm C、6cm D、8cm6. 华为麒麟990芯片采用了最新的0.000000007米的工艺制程,0.000000007用科学记数法表示为( )A、7×10-9 B、7×10-8 C、0.7×10-9 D、0.7×10-87. 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( ) A、12 B、8 C、15 D、138. 从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其截成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙),那么通过计算两个图形阴影部分的面积,可以验证成立的式子为( )
A、12 B、8 C、15 D、138. 从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其截成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙),那么通过计算两个图形阴影部分的面积,可以验证成立的式子为( )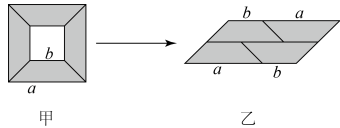 A、(a+b)2=a2+2ab+b2 B、(a- b)2= a2-2ab+b2 C、a2- b2=(a+b) (a- b) D、(a+2b) (a+b)= a2+3ab+2b29. 如图,在△ABC中,∠ACB=90",按如下步骤操作:1以点A为圆心,任意长为半径作弧,分别交AC,AB于D,E两点;②以点C为圆心,AD长为半径作弧,交AC的延长线于点F;③以点F为圆心,DE长为半径作弧,交②中所画的弧于点G;④作射线CG,若∠B=40°,则∠FCG为( )
A、(a+b)2=a2+2ab+b2 B、(a- b)2= a2-2ab+b2 C、a2- b2=(a+b) (a- b) D、(a+2b) (a+b)= a2+3ab+2b29. 如图,在△ABC中,∠ACB=90",按如下步骤操作:1以点A为圆心,任意长为半径作弧,分别交AC,AB于D,E两点;②以点C为圆心,AD长为半径作弧,交AC的延长线于点F;③以点F为圆心,DE长为半径作弧,交②中所画的弧于点G;④作射线CG,若∠B=40°,则∠FCG为( )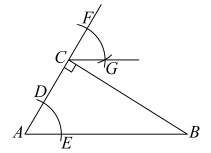 A、40° B、50° C、60° D、70°10. 如图,在等边△PQB中,点A为PQ上一动点(不与P,Q重合),再以AB为边作等边△ABC,连接PC.有以下结论:①PB平分∠ABC;②AQ=CP;③PC//QB;④PB=PA+PC;⑤当 BC⊥BQ时,△ABC的周长最小,其中一定正确的有( )
A、40° B、50° C、60° D、70°10. 如图,在等边△PQB中,点A为PQ上一动点(不与P,Q重合),再以AB为边作等边△ABC,连接PC.有以下结论:①PB平分∠ABC;②AQ=CP;③PC//QB;④PB=PA+PC;⑤当 BC⊥BQ时,△ABC的周长最小,其中一定正确的有( )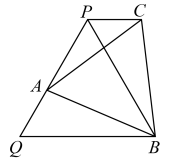 A、①②③ B、②③④ C、③④⑤ D、②③④⑤
A、①②③ B、②③④ C、③④⑤ D、②③④⑤二、填空题(本大题5小题,每小题3分,共15分)
-
11. 点P(-2,3)关于x轴的对称点的坐标是 .12. 计算:(-) - 2 - (π-3.14)0=13. 已知一个n边形的每一个外角都为30°,则n等于 .14. 因式分解2x2- 12x +18的结果是15. 在第1个△ABA1中,∠B=30,AB=A1B,在A1B上取一点C,延长AA1到A2 , 使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3 , 使得A2A3=A2D;...,按此做法进行下去,第n个三角形的以An为顶点的内角的度数为

三、解答题(一)(本大题4小题,第16、17题各5分,第18、19题各7分,共24分)
-
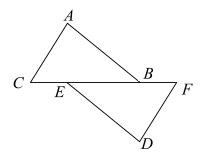
16. 计算:(a+4) (a- 4) - (a- 1)2.17. 如图,点C、E、B、F在同一直线上,AC//DF,AC=DF,BC=EF
求证:AB=DE
 18. 解分式方程: .19. 先化简,再求值: , 其中a=1
18. 解分式方程: .19. 先化简,再求值: , 其中a=1四、解答题(二)(本大题3小题,每小题9分,共27分)
-
20. 如图,已知∠B=∠E=90°,AB=DE,AF=CD,BC与EF交于点G.
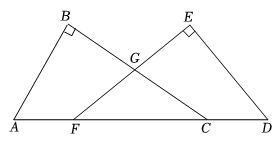 (1)、求证:BC=EF;(2)、若∠A=50°,求∠BGF的度数.21. 如图,在平面直角坐标系中,△ABC 的三个顶点坐标分别为A(1,- 4),B (3,- 3) ,
(1)、求证:BC=EF;(2)、若∠A=50°,求∠BGF的度数.21. 如图,在平面直角坐标系中,△ABC 的三个顶点坐标分别为A(1,- 4),B (3,- 3) ,C(1,- 1).
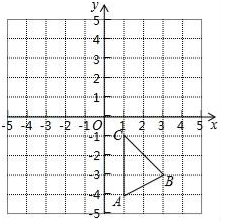 (1)、画出△ABC关于x轴对称的△A1B1C1;(2)、写出△A1B1C1各顶点的坐标;(3)、求△ABC 的面积.22. 为增强学生体质,很多学校决定在课后看护中增加乒乓球项目,体育用品商店得知后,第一次用600元购进乒乓球若干盒,第二次又用600元购进该款乒乓球,但这次每盒的进价比第一次的进价高25%,购进数量比第一次少了30盒.(1)、求第一次每盒乒乓球的进价是多少元?(2)、若要求这两次购进的乒乓球按同一价格全部销售完后获利不低于420元,求每盒乒乓球的售价至少是多少元?
(1)、画出△ABC关于x轴对称的△A1B1C1;(2)、写出△A1B1C1各顶点的坐标;(3)、求△ABC 的面积.22. 为增强学生体质,很多学校决定在课后看护中增加乒乓球项目,体育用品商店得知后,第一次用600元购进乒乓球若干盒,第二次又用600元购进该款乒乓球,但这次每盒的进价比第一次的进价高25%,购进数量比第一次少了30盒.(1)、求第一次每盒乒乓球的进价是多少元?(2)、若要求这两次购进的乒乓球按同一价格全部销售完后获利不低于420元,求每盒乒乓球的售价至少是多少元?五、解答题(三)(本大题2小题,每小题12分,共24分)
-
23. 图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图2拼成一个正方形.
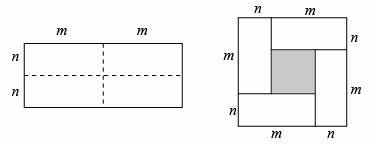
图1 图2
(1)、直接写出图2中阴影部分的正方形的边长为(2)、观察图2,请直接写出下列三个代数式(m+n) 2 , (m- n) 2 , mn之间的等量关系是(3)、根据(2)中的等量关系,解决如下问题:①若 p+q=9,pq=7,求(p- q) 2的值:
②若(2021- a) 2+( a - 2022) 2=7,求(2021- a) ( a- 2022)的值.
24. 如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(m,0)、B(0,n),且︱m- n- 3︱+(2n- 6)2=0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P运动时间为t秒.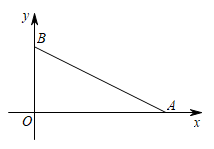 (1)、OA= , OB=(2)、连接 PB,若△POB的面积为3,求t的值(3)、过P作直线AB的垂线,垂足为D,直线PD与y轴交于点E,在点P运动的过程中,是否存在这样点P,使△EOP≌△AOB,若存在,请直接写出t的值;若不存在,请说明理由.
(1)、OA= , OB=(2)、连接 PB,若△POB的面积为3,求t的值(3)、过P作直线AB的垂线,垂足为D,直线PD与y轴交于点E,在点P运动的过程中,是否存在这样点P,使△EOP≌△AOB,若存在,请直接写出t的值;若不存在,请说明理由.