2024年浙教版数学八年级下册3.3方差和标准差课后提高练
试卷更新日期：2024-03-15 类型：同步测试
一、选择题
-
1. 若数据1，2，3，4，5的方差是a，则数据7，8，9，10，11的方差是 （ ）A、a B、2a C、4a D、5a2. 已知一组数据2，5，4，x，3的平均数是4，则这组数据的标准差是（ ）A、4 B、2 C、 D、3. 已知一组数据x₁，x₂，x₃，平均数是2，方差是3，则另一组数2x₁-1，2x₂-1，2x₃-1的平均数和方差分别是 （ ）A、2， B、3，3 C、3，12 D、3，44. 甲、乙两人在相同的条件下，各射击10次，经计算：甲射击成绩的平均数是8环，方差是1.1环²，乙射击成绩的平均数是8环，方差是1.5环².下列说法中不一定正确的是（ ）A、甲、乙的总环数相同 B、甲的成绩比乙的成绩稳定 C、乙的成绩比甲的成绩波动大 D、甲、乙成绩的众数相同5. A，B两名射击运动员进行了相同次数的射击，下列关于他们射击成绩的平均数和方差的描述中，能说明A成绩较好且更稳定的是（ ）A、>且> B、<且> C、>且< D、<且<6. 已知一组数据的方差是3，则这组数据的标准差是（ ）A、3 B、± C、 D、7. 初中三年学习生涯，让懵懂青涩的少年逐渐成长为奋发向上的青年．比较九班名同学三年前后的年龄数据，在平均数、众数、中位数和方差四个统计量中，大小没有发生变化的统计量是（ ）A、平均数 B、众数 C、中位数 D、方差8. 在日常生活中，对某些技能的训练，新手的表现通常不太稳定．以下是四名学生进行8次射击训练之后的成绩统计图，请根据图中信息估计最可能是新手的是（ ）A、
B、
C、
D、
二、填空题
-
9. 若一组数据 4，x，5，y，7，9 的平均数是6，众数是5，则这组数据的方差是.10. 已知一组数据x₁，x₂，x₃，…，x。的方差是 1.5，则另一组 数 据 2x₁，2x₂， 2x₃，…，2x， 的方差是.11. 教练对跳远运动员小刚的训练效果进行了测试，6次跳远的成绩(单位：m)如下：7.6，7.8，7.7，7.8，8.0，7.9.这6次成绩的平均数是7.8m，方差是 m².若小刚再跳两次，成绩分别是7.7，7.9，则小刚这8次跳远成绩的方差将(填“变大”“变小”或“不变”).12. “共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献．全球共有40多个国家引种杂交水稻，中国境外种植面积达800万公顷．某村引进了甲、乙两种超级杂交水稻品种，在条件（肥力、日照、通风……）不同的6块试验田中同时播种并核定亩产，统计结果为：/亩，﹐/亩， ， 则品种更适合在该村推广．（填“甲”或“乙”）
三、解答题
-
13. 为提高学生的数学思维能力，某中学开展“迎元旦数学知识竞赛”，八(1)班、八(2)班各选出5名选手参加竞赛，整理5名选手的竞赛成绩(满分为100分)绘制如图所示的统计图和不完整的统计表．
平均数
中位数
众数
八(1)班(分)
87
80
八(2)班(分)
85
(1)、请你把表格补充完整；(2)、结合两班竞赛成绩的平均数中位数和众数，你认为哪个班的竞赛成绩较好；(3)、计算两个班竞赛成绩的方差，并说明哪个班的成绩较为整齐．14. 为贯彻习近平总书记提出的“绿水青山就是金山银山”的重要思想，某校举办了“绿水青山，生态文明”知识竞赛(每一项的满分为 10分，得分均为整数).在这次竞赛中张山与李仕两位同学表现优秀，他们的四项成绩分布的条形统计图如图所示，根据该图解答下列问题.两位同学四项成绩分布的条形统计图
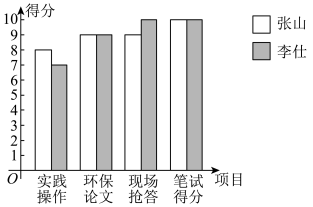(1)、完成下表：姓名
平均数(分)
中位数(分)
众数(分)
方差(分2)
张山
9
9
李仕
9.5
1.5
(2)、根据(1)中数据，分别从中位数、方差两个角度比较分析两位同学各自的优势.(3)、若实践操作、环保论文、现场抢答、笔试得分按4：1：2：3的比例折合成综合得分，请通过计算说明哪位同学的综合得分更高.15. 为比较营养液和营养液对某种小西红柿产量的影响，甲、乙两个生物小组各选取了10株长势相近的小西红柿秧苗进行对照实验．甲组使用营养液 ， 乙组使用营养液 ． 将每株的产量记录整理，并绘制了如下两个条形图．
解答下列问题：
(1)、甲组产量的中位数为 ， 乙组每株产量的众数为；(2)、为了使产量更稳定，请计算两组产量的平均数，再结合条形图，则应选择营养液；（填“”或“”）；(3)、产量30个及以上为秧苗长势良好．现在选用第（2）问推荐的营养液培育1000株秧苗，请估计长势良好的大约有多少株？