贵州省贵阳市乌当区2023-2024学年八年级上学期期末数学试卷

试卷更新日期：2024-03-15 类型：期末考试

进入出卷网下载

一、选择题：以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请在答题卡相应位置作答，每小题3分，共36分.

1. 下列几组数中，能构成直角三角形三边长的是（）

A、1，2，3 B、2，3，4 C、3，4，5 D、4，5，6

查看试题解析
2. 下列计算错误的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ C、 $\sqrt{15} \div \sqrt{3} = \sqrt{5}$ D、 $\sqrt{3^{2}} = 3$

查看试题解析
3. 将直角坐标系中的点（﹣1，﹣3）向上平移4个单位，再向右平移2个单位后的点的坐标为（　　）

A、（3，﹣1） B、（﹣5，﹣1） C、（﹣3，1） D、（1，1）

查看试题解析
4. 甲、乙、丙、丁四人进行射箭测试，每人测试10次，射箭成绩的平均数都是8.8环，方差分别为 $s_{甲}^{2} = 0.65$ ， $s_{乙}^{2} = 0.45$ ， $s_{丙}^{2} = 0.55$ ， $s_{丁}^{2} = 0.50$ ，则射箭成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 下列四个命题中，真命题是（　　）

A、两条直线被第三条直线所截，内错角相等 B、如果x²＞0，那么x＞0 C、如果∠1和∠2是对顶角，那么∠1＝∠2 D、三角形的一个外角大于任何一个内角

查看试题解析
6. 在直角坐标系中，已知点A（ $\frac{2}{3}$ ， m），点B（3，n）是直线y＝﹣2x+1上的两点，则m ， n的大小关系是（　　）

A、m＜n B、m＞n C、m≥n D、m≤n

查看试题解析
7. 母亲节来临，小明去花店为妈妈准备节日礼物．已知康乃馨每支2元，百合每支3元．小明将20元钱全部用于购买这两种花（两种花都买），小明的购买方案共有（　　）

A、2种 B、3种 C、4种 D、5种

查看试题解析
8. 若m，n是两个连续的整数且 $m < \sqrt{14} < n$ ，则m+n＝（）

A、5 B、6 C、7 D、8

查看试题解析
9. 如图所示的“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．该图由四个全等的直角三角形和一个小正方形拼成一个大正方形，设直角三角形较长直角边长为a ，较短直角边长为b ．若ab＝10，大正方形面积为25，则小正方形边长为（　　）

A、 $\sqrt{3}$ B、2 C、 $\sqrt{5}$ D、3

查看试题解析
10. 关于x ， y的方程组 $\{\begin{array}{l} x + p y = 0 \\ x + y = 3 \end{array}$ 的解是 $\{\begin{array}{l} x = 1 \\ y = ▲ \end{array}$ ，其中y的值被盖住了，不过仍能求出p ，则p的值是（　　）

A、- $\frac{1}{2}$ B、 $\frac{1}{2}$ C、﹣ $\frac{1}{4}$ D、 $\frac{1}{4}$

查看试题解析
11. 某市为了方便市民绿色出行，推出了共享单车服务．图①是某品牌共享单车放在水平地面的实物图，图②是其示意图，其中 $A B$ ， $C D$ 都与地面l平行， $∠ B C D = 60 °$ ， $∠ B A C = 54 °$ ．当 $∠ M A C$ 为（）度时， $A M$ 与 $C B$ 平行．

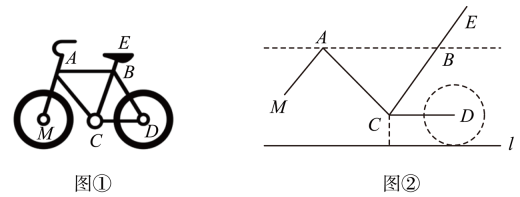A、16 B、60 C、66 D、114

查看试题解析
12. 甲、乙两人沿同一直道从 $A$ 地到 $B$ 地，在整个行程中，甲、乙离 $A$ 地的距离 $S$ 与时间 $t$ 之间的函数关系如图所示，下列说法错误的是（）

A、甲比乙早1分钟出发 B、乙的速度是甲的速度的2倍 C、若甲比乙晚5分钟到达，则甲用时10分钟 D、若甲出发时的速度为原来的2倍，则甲比乙提前1分钟到达 $B$ 地

查看试题解析

二、填空题：每小题4分，共16分.

13. 若代数式 $\sqrt{x + 3}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
14. 把命题“对顶角相等”改写成“如果…那么…”的形式：

查看试题解析
15. 关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} - k x + y = b \\ - m x + y = n \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ ，则直线 $A B$ ： $y = k x + b$ 与直线 $C D$ ： $y = m x + n$ 的交点坐标为．

查看试题解析
16. 如图，在△ABC中，AB＝AC＝5，观察尺规作图的痕迹，若BE＝2，则BC的长是．

查看试题解析

三、解答题：解答应写出文字说明，演算步骤或证明过程，6小题，共48分.

17. 计算：

(1)、 $(2024 - π)^{0} - {(\frac{1}{2})}^{- 1} + \sqrt{8}$ ；

(2)、解方程组： $\{\begin{array}{l} x - 2 y = - 3 \\ 2 x + y = 9 \end{array}$ ．

查看试题解析
18. 如图，点F在线段AB上，点E ， G在线段CD上，AB∥CD ， ∠1＝∠2．

(1)、求证：FG∥AE；

(2)、若FG⊥BC于点H ， BC平分∠ABD ， ∠D＝120°，求∠1的度数．

查看试题解析
19. 如图所示，在平面直角坐标系中，已知A（0，1）、B（2，0）、C（4，3）．

(1)、在平面直角坐标系中画出△ABC ，并画出△ABC关于y轴对称的△AB₁C₁ ，

(2)、已知P为x轴上一点，若△ABP的面积为4，求点P的坐标．

查看试题解析
20. 习近平总书记指出，“红色是中国共产党、中华人民共和国最鲜亮的底色”，要用好红色资源，赓续红色血脉，为引导广大青少年树立正确的世界观、人生观、价值观，传承红色基因，某校组织了一次以“赓续红色血脉，强国复兴有我”为主题的演讲比赛，比赛成绩分为以下5个等级：A.100分、B.90分、C.80分、D.70分、E.60分，比赛结束后随机抽取部分参赛选手的成绩，整理并绘制成如图统计图，请你根据统计图解答下列问题：

(1)、所抽取学生比赛成绩的众数是分，中位数是人分；

(2)、求所抽取学生比赛成绩的平均数；

(3)、若参加此次比赛的学生共100名，且学校计划为比赛成绩进入A、B两个等级的学生购买奖品，请估计学校共需要准备多少份奖品？

查看试题解析
21. 高州市在创建“全国文明城市”期间，某小区在临街的拐角清理出了一块可以绿化的空地．如图，经技术人员的测量，已知AB＝9m ， BC＝12m ， CD＝17m ， AD＝8m ， ∠ABC＝90°．

(1)、求空地的面积；

(2)、若平均每平方米空地的绿化费用为150元，试计算绿化这片空地共需花费多少元？

查看试题解析
22. 某体育用品商店销售一种品牌的羽毛球拍和配套的羽毛球，购买一副羽毛球拍和一筒羽毛球共需60元，购买两幅羽毛球拍和3筒羽毛球共需130元．

(1)、求每副羽毛球拍和每筒羽毛球的价钱；

(2)、春季运动会召开前夕，该商店开展了两种优惠促销活动，具体办法如下：
活动甲：买一副羽毛球拍送一筒羽毛球；
活动乙：按购买金额打9折付款．
学校欲购买这种羽毛球拍10副，羽毛球x（x≥10）筒．
①写出每种优惠办法实际付款金额y_甲（元），y_乙（元）与x（筒）之间的函数关系式．
②比较购买同样多的羽毛球时，按哪种优惠付款更省钱？

查看试题解析