广西南宁市2023-2024学年七年级上学期期末数学试卷
试卷更新日期:2024-03-14 类型:期末考试
一、选择题(共12小题,每小题3分,共36分.每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑.)
-
1. 数2的倒数是( )A、-2 B、2 C、- D、2. 如图,尉迟恭单鞭救主图罐是南宁博物馆的镇馆之宝,下列平面图形绕轴旋转一周能形成这个瓷罐形状的是( )
 A、
A、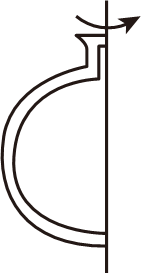 B、
B、 C、
C、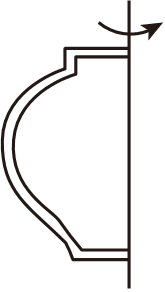 D、
D、 3. 2023年11月15日第一届全国学生(青年)运动会在南宁开幕,为保障比赛顺利进行,组委会从多所高校招募了16500名志愿者,其中数据16500用科学记数法表示为( )A、0.165×105 B、1.65×104 C、1.65×105 D、16.5×1034. 如图,检测4个排球,其中质量超过标准的克数记为正数,不足的克数记为负数,从轻重的角度,下列最接近标准的是( )
3. 2023年11月15日第一届全国学生(青年)运动会在南宁开幕,为保障比赛顺利进行,组委会从多所高校招募了16500名志愿者,其中数据16500用科学记数法表示为( )A、0.165×105 B、1.65×104 C、1.65×105 D、16.5×1034. 如图,检测4个排球,其中质量超过标准的克数记为正数,不足的克数记为负数,从轻重的角度,下列最接近标准的是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 下列各式中,次数为5的单项式是( )A、x2 B、x3y2 C、3xy D、x3+y36. 如图,射线 表示的方向是( )
5. 下列各式中,次数为5的单项式是( )A、x2 B、x3y2 C、3xy D、x3+y36. 如图,射线 表示的方向是( ) A、北偏东 B、北偏西 C、南偏东 D、南偏西7. 如图,数轴上点A和点B分别表示数a和b,则下列式子正确的是( )
A、北偏东 B、北偏西 C、南偏东 D、南偏西7. 如图,数轴上点A和点B分别表示数a和b,则下列式子正确的是( ) A、a>0 B、ab>0 C、a-b>0 D、a+b<08. 已知x=y,根据等式的性质下列变形正确的是( )A、x=2y B、x+1=y+2 C、x-3=y-3 D、9. 一件衣服的进价是100元,如果卖出后盈利25%,则这件衣服的售价是( )A、110元 B、115元 C、120元 D、125元10. 如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
A、a>0 B、ab>0 C、a-b>0 D、a+b<08. 已知x=y,根据等式的性质下列变形正确的是( )A、x=2y B、x+1=y+2 C、x-3=y-3 D、9. 一件衣服的进价是100元,如果卖出后盈利25%,则这件衣服的售价是( )A、110元 B、115元 C、120元 D、125元10. 如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( ) A、
A、 B、
B、 C、
C、 D、
D、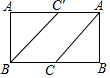 11. 中国一本著名数学文献《九章算术》,书中出现了一个“共买鸡问题”,原文是:今有共买鸡,人出九,盈十一;人出六,不足十六,问人数、物价各几何?其题意是:有若干人一起买鸡,如果每人出9文钱,就多出11文钱;如果每人出6文钱,就相差16文钱.问买鸡的人数、鸡的价钱各是多少?设买鸡的人数为x,则下面符合题意的方程是( )A、9x+11=6x-16 B、9x+6x=16+11 C、9x+11=6x+16 D、9x-11=6x+1612. 如图,图中都是由大小和形状完全相同的小四边形按照一定的规律排列组成,其中第①个图形中一共有1个小四边形,第②个图形中一共有3个小四边形,第③个图形中一共有6个小四边形,…,按此规律排列下去,第⑤个图形中小四边形的个数是( )
11. 中国一本著名数学文献《九章算术》,书中出现了一个“共买鸡问题”,原文是:今有共买鸡,人出九,盈十一;人出六,不足十六,问人数、物价各几何?其题意是:有若干人一起买鸡,如果每人出9文钱,就多出11文钱;如果每人出6文钱,就相差16文钱.问买鸡的人数、鸡的价钱各是多少?设买鸡的人数为x,则下面符合题意的方程是( )A、9x+11=6x-16 B、9x+6x=16+11 C、9x+11=6x+16 D、9x-11=6x+1612. 如图,图中都是由大小和形状完全相同的小四边形按照一定的规律排列组成,其中第①个图形中一共有1个小四边形,第②个图形中一共有3个小四边形,第③个图形中一共有6个小四边形,…,按此规律排列下去,第⑤个图形中小四边形的个数是( ) A、12 B、13 C、14 D、15
A、12 B、13 C、14 D、15二、填空题(本大题共6小题,每小题2分,共12分)
-
13. |-4|= .14. 用四舍五入法取近似值:9.527≈(精确到0.01).15. 如图,把原来弯曲的河道改直,两地间的河道长度会变短,这其中蕴含的数学道理是 .
 16. 一个角的度数是30°,则它的余角为 度.17. 如图,点C是线段AB上一点,AB=8cm,AC=2cm,则BC= cm.
16. 一个角的度数是30°,则它的余角为 度.17. 如图,点C是线段AB上一点,AB=8cm,AC=2cm,则BC= cm. 18. 幻方是非常古老的数学问题,其要求将9个数分别填入图中9个格中,使得处于每一横行、每一竖列以及两条斜对角线上的3个数字之和都相等.请你将数字-4,-3,-2,-1,0,1,2,3,4分别填入如图所示的幻方中,那么“♥”所在的格中应填的数字是 .
18. 幻方是非常古老的数学问题,其要求将9个数分别填入图中9个格中,使得处于每一横行、每一竖列以及两条斜对角线上的3个数字之和都相等.请你将数字-4,-3,-2,-1,0,1,2,3,4分别填入如图所示的幻方中,那么“♥”所在的格中应填的数字是 .1
3
0
♥
三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
19. 计算:(1)、(+1)+(-5)-(-9)+(+4);(2)、(-1)×(-6)+22÷(7-5).20. 解方程:(1)、3x-2=8+x;(2)、 .21. 先化简,再求值:2(3a2b-a)-(3a2b-2a),其中a=2,b= .22. 如图,已知点A,B和线段m.
 (1)、用圆规和直尺作图,保留作图痕迹,不写作法,标明字母.
(1)、用圆规和直尺作图,保留作图痕迹,不写作法,标明字母.
①连接AB;
②延长AB到点C,使BC=AB;
③在线段AB上作线段AD=m;(2)、在(1)的条件下,若AB=5,m=3,求CD的长.23. 某公司在直播间推广壮族绣球文化,同时销售壮族绣球,规定每天销量超过100个的部分记为“+”,低于100个的部分记为“-”,如表是该公司一周的销售情况:周一
周二
周三
周四
周五
周六
周日
销量(个)
10
12
-15
-6
14
-18
13
(1)、该公司本周共销售绣球多少个?(2)、每个绣球售价定为20元,求该公司本周的总销售额.24. 实验与操作:
【课本回顾】如图1,我们通过折纸可以找出一个角的平分线,射线QT即是∠PQR的平分线.
【操作实践】如图2,将长方形纸片ABCD沿OC折叠,点B落在点B'处,设∠BOC=x. (1)、若x=35°,求∠AOB'的度数;(2)、【拓广探索】如图3,在图2的基础上,再将长方形纸片ABCD沿OD折叠,点A落在点A处,边OA'在OB'的左侧,若此时OB'平分∠BOD.
(1)、若x=35°,求∠AOB'的度数;(2)、【拓广探索】如图3,在图2的基础上,再将长方形纸片ABCD沿OD折叠,点A落在点A处,边OA'在OB'的左侧,若此时OB'平分∠BOD.
求∠AOD(用含x的式子表示);(3)、若∠A'OB'=12°,请直接写出x的度数.25. 学校举办了迎新春中国象棋比赛,以下是部分选手的积分记录表:选手
比赛总局数
胜局
平局
负局
积分
A
12
12
0
0
36
B
12
7
3
2
22
C
12
5
4
3
16
D
12
6
0
6
12
(1)、请直接写出胜一局、平一局、负一局分别积几分;(2)、已知某选手E的负局数是胜局数的一半,他的胜局积分能等于平局积分的四倍吗?为什么?26. 综合与实践【问题提出】随着时间的变化,钟面上时针和分针形成夹角的度数也随之变化,记时针和分针的夹角为α(a大于等于 0°,且小于等于 180° ).我们可以求出任意时刻∠α 的度数吗?
分针运动规律
分针每分钟走6° 
时针运动规律
时针每小时走30°即每分钟走0.5° 规定
当时针和分针指向刻度12记为0° 特例探究1(8点50分)
分针绕点O旋转所得角的度数是6°×50=300°,时针绕点O旋转所得角的度数是30°×8+0.5°×50=265°所以∠α=300°-265°=35°. 
特例探究2(8时30分)
分针绕点O旋转所得角的度数是6°×30=180°,时针绕点O旋转所得角的度数是30°×8+0.5°×30=255°所以.∠α=255°-180°=75°.  .
. 特例探究3(8时10分)
分针绕点O旋转形成的角的度数是6°×10=60°,时针绕点O旋转形成的角的度数是30°×8+0.5°×10=245°,此时245°-60°=185°,由于185°>180°,所以∠α=360°-185°=175°.  (1)、当时间为7时30分时,请你求出∠α的度数;(2)、王老师7时整从家中出门散步,当她返回家中时还不到8时,此时她发现时针与分针形成的夹角正好是直角求王老师外出散步用了多少分钟?
(1)、当时间为7时30分时,请你求出∠α的度数;(2)、王老师7时整从家中出门散步,当她返回家中时还不到8时,此时她发现时针与分针形成的夹角正好是直角求王老师外出散步用了多少分钟?