广东省江门市江海区2023-2024学年七年级上学期期末数学试题
试卷更新日期:2024-03-14 类型:期末考试
一、选择题(本大题包括10小题,每小题3分,共30分)
-
1. 中国空间站梦天实验舱近地轨道距地面约390000米,数据390000用科学记数法表示为( )A、 B、 C、 D、2. 下列生产或生活现象中,可以用基本事实“两点之间线段最短”来解释的是( )A、用两枚钉子可以把一根木条固定在墙上 B、植树时,只要定出两棵树的位置,就能确定同一行树所在的直线 C、建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙 D、把弯曲的公路改直,就能缩短路程3. 下列计算中,正确的是( )A、|﹣2|=﹣2 B、(﹣1)2=﹣2 C、﹣7+3=﹣4 D、6÷(﹣2)=34. 下列各组中的两项,属于同类项的是( )A、与 B、与 C、与 D、与5. 已知x=2是关于x的一元一次方程mx+2=0的解,则m的值为( )A、﹣1 B、0 C、1 D、26. 将一副直角三角尺如图放置,若 , 则的大小为( )
 A、 B、 C、 D、7. 下列各图经过折叠后不能围成一个正方体的是( )A、
A、 B、 C、 D、7. 下列各图经过折叠后不能围成一个正方体的是( )A、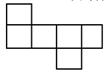 B、
B、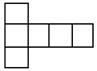 C、
C、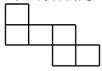 D、
D、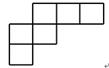 8. 如图,已知轮船A在灯塔P的北偏东方向,轮船B在灯塔P的南偏东方向,则的度数是( )
8. 如图,已知轮船A在灯塔P的北偏东方向,轮船B在灯塔P的南偏东方向,则的度数是( )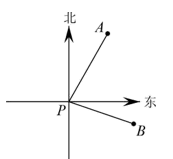 A、 B、 C、 D、9. 观察下列一组数: , …,它们是按一定规律排列的,那么这一组数的第个数是( )A、 B、 C、 D、10. 如图所示,圆的周长为个单位长度,在圆周的等分点处标上字母 , 先将圆周上的字母对应的点与数轴的数字所对应的点重合,若将圆沿着数轴向左滚动、那么数轴上的所对应的点与圆周上重合的字母是( )
A、 B、 C、 D、9. 观察下列一组数: , …,它们是按一定规律排列的,那么这一组数的第个数是( )A、 B、 C、 D、10. 如图所示,圆的周长为个单位长度,在圆周的等分点处标上字母 , 先将圆周上的字母对应的点与数轴的数字所对应的点重合,若将圆沿着数轴向左滚动、那么数轴上的所对应的点与圆周上重合的字母是( )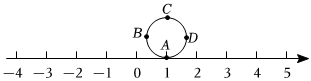 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题包括6小题,每小题3分,共18分)
-
11. 比较大小:﹣5﹣8(填“>”或“<”号)12. 的相反数是 .13. 已知∠1与互补, , 则°14. 若 , 则 .15. 已知 , , 则的值为 .16. 按如图所示程序计算,若最终输出的结果为 , 则输入的正整数x是 .

三、解答题(一)(本大题4小题,17、18每小题6分,19、20每小题8分,共28分)
-
17. 计算: .18. 计算: .19. 解方程: .20. 先化简下式,再求值 , 其中
四、解答题(二)(本大题包括3小题,每小题8分,共24分)
-
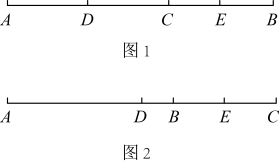
21. 如图,A、B、C三点在同一条直线上,点是线段的中点,点是线段的中点.
 (1)、如图1,点在线段上,若 , , 求线段的长;(2)、如图2,点在线段的延长线上,若 , 求线段的长.22. 已知: , .(1)、计算: ;(2)、若 的值与字母 的取值无关,求 的值.23. 某工厂要制作一批糖果盒,已知该工厂共有88名工人,其中女工人数比男工人数的2倍少20人,并且每个工人平均每小时可以制作盒身50个或盒底120个.(1)、该工厂有男工、女工各多少人?(2)、该工厂原计划男工负责制作盒身,女工负责制作盒底,要求一个盒身配两个盒底,那么调多少名女工帮男工制作盒身时,才能使每小时制作的盒身与盒底恰好配套?
(1)、如图1,点在线段上,若 , , 求线段的长;(2)、如图2,点在线段的延长线上,若 , 求线段的长.22. 已知: , .(1)、计算: ;(2)、若 的值与字母 的取值无关,求 的值.23. 某工厂要制作一批糖果盒,已知该工厂共有88名工人,其中女工人数比男工人数的2倍少20人,并且每个工人平均每小时可以制作盒身50个或盒底120个.(1)、该工厂有男工、女工各多少人?(2)、该工厂原计划男工负责制作盒身,女工负责制作盒底,要求一个盒身配两个盒底,那么调多少名女工帮男工制作盒身时,才能使每小时制作的盒身与盒底恰好配套?五、解答题(三)(本大题包括2小题,每小题10分,共20分)
-
24. 为了鼓励居民节约用水,某市自来水公司按如下方式对每户月用水量进行计费:当用水量不超过10吨时,每吨的收费标准相同;当用水量超过10吨时,超出10吨的部分每吨收费标准也相同.下表是小明家1﹣4月份用水量和交费情况:
月份
1
2
3
4
用水量(吨)
8
10
12
15
费用(元)
16
20
26
35
请根据表格中提供的信息,回答以下问题:
(1)、若小明家5月份用水量为20吨,则应缴水费多少元?(2)、若小明家6月份交纳水费29元,则小明家6月份用水多少吨?25. 新定义:如果的内部有一条射线将分成的两个角,其中一个角是另一个角的n倍,那么我们称射线为的n倍分线,例如,如图1, , 则为的4倍分线. , 则也是的4倍分线. (1)、应用:若 , 为的二倍分线,且则°;(2)、如图2,点A , O , B在同一条直线上为直线上方的一条射线.
(1)、应用:若 , 为的二倍分线,且则°;(2)、如图2,点A , O , B在同一条直线上为直线上方的一条射线.①若 , 分别为和的三倍分线,( , )已知, , 则_▲_°;
②在①的条件下,若 , 的度数是否发生变化?若不发生变化,请写出计算过程;若发生变化,请说明理由.
③如图3,已知 , 且 , 所在射线恰好是分别为和的三倍分线,请直接写出的度数.