广东省阳江市阳春市2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-03-14 类型：期末考试

进入出卷网下载

一、单选题

1. $- 2023$ 的相反数是（　　）

A、2023 B、 $- \frac{1}{2023}$ C、 $\frac{1}{2023}$ D、 $- 2023$

查看试题解析
2. 港珠澳大桥是世界上最长的跨海大桥，被称为“新世界七大奇迹之一”，其总长度为55000米，则数据55000用科学记数法表示为（）

A、 $55 \times 1 0^{5}$ B、 $5.5 \times 1 0^{4}$ C、 $0.55 \times 1 0^{5}$ D、 $5.5 \times 1 0^{5}$

查看试题解析
3. 如图所示，钟表上的时间下午 $3 ： 30$ 时，时针与分针之间所成的角是（）

A、 $75 °$ B、 $70 °$ C、 $65 °$ D、 $60 °$

查看试题解析
4. 下列变形，其中不正确的为（）

A、如果 $a = b$ ，那么 $a + 1 = b + 1$ B、如果 $a = b$ ，那么 $a - 5 = b - 5$ C、如果 $a = b$ ，那么 $a c = b c$ D、如果 $a = b$ ，那么 $\frac{a}{c} = \frac{b}{c}$

查看试题解析
5. 用一副三角板（两块）画角，不可能画出的角的度数是（）

A、 $75 °$ B、 $85 °$ C、 $135 °$ D、 $105 °$

查看试题解析
6. 如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“建”字一面的相对面上的字是（）

A、和 B、谐 C、社 D、会

查看试题解析
7. 如图，把原来弯曲的河道改直，A ， B两地间的河道长度变短，这样做的道理是（）

A、两点确定一条直线 B、两点之间线段最短 C、两点之间直线最短 D、线段是直线的一部分

查看试题解析
8. 对于如图所示的几何体，说法正确的是（）

A、几何体是三棱锥 B、几何体有6条侧棱 C、几何体的侧面是三角形 D、几何体的底面是三角形

查看试题解析
9. “3•15晚会”曝光了专骗老人买神药的“直播间儿子”一一将成本价1.2元/盒的产品卖到10盒/99元．该产品的利润率约为（）

A、 $825 %$ B、 $12.1 %$ C、 $725 %$ D、 $87.9 %$

查看试题解析
10. 如图，表中给出的是某月的日历，任意选取“U”型框中的7个数（如阴影部分所示），请你运用所学的数学知识来研究，发现此月这7个数的和可能的是（）

A、106 B、98 C、84 D、78

查看试题解析

二、填空题

11. 请写出一个比 $- 4$ 大的负整数：．

查看试题解析
12. 若单项式 $x^{a + 3} y$ 与 $- 5 x y^{b}$ 是同类项，则 ${(a + b)}^{2023} =$ ．

查看试题解析
13. 若代数式 $5 x - 1$ 的值与 $- 2$ 互为相反数，则 $x =$ ．

查看试题解析
14. 每筐杨梅以4千克为基准，超过的千克数记为正数，不足的千克数记为负数，记录如图，则这4筐杨梅的总质量是千克．

查看试题解析
15. 一个两位数个位上的数是1，十位上的数是 $x$ ，把1与 $x$ 对调，新两位数比原两位数小18，依题意，可列出方程．

查看试题解析
16. 如图，用火柴棍拼成一排由三角形组成的图形，如果图形中含有n个三角形，则需要根火柴棍。

查看试题解析

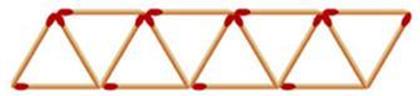
三、解答题

17. 计算：

(1)、 $- 8 + 4 \div (- 2)$

(2)、 $- 1^{4} - \frac{1}{6} \times [2 - (- 3)^{2}]$

查看试题解析
18. 解方程： $\frac{x + 1}{2} - 2 = \frac{x}{4}$

查看试题解析
19. A、B两地相距480千米，一列慢车从A地出发，每小时走60千米，一列快车从B地出发，每小时走105千米，慢车出发1小时后快车从B地出发，同向而行，请问快车出发几小时后追上慢车？

查看试题解析
20. 如图：已知线段 $A B = 16 cm$ ，点 $N$ 在线段 $A B$ 上， $N B = 3 cm$ ， $M$ 是 $A B$ 的中点．

(1)、求线段 $M N$ 的长度；

(2)、若在线段 $A B$ 上有一点 $C$ ，满足 $B C = 10 cm$ ，求线段 $M C$ 的长度．

查看试题解析
21. 如图，已知 $O$ 是直线 $A B$ 上的一点， $∠ C O D$ 是直角， $O E$ 平分 $∠ B O C$ ．

(1)、若 $∠ A O C = 30 °$ ，求 $∠ D O E$ 的度数；

(2)、若 $∠ A O C = α$ ，求 $∠ D O E$ 的度数（用含 $α$ 的代数式表示）．

查看试题解析
22. 公交车从起点经过东湖广场站、朝南路站、中心广场站、妇幼医院站到达终点，一路上下乘客如表所示．（用正数表示上车的人数，负数表示下车的人数）

起点
东湖广场站
朝南路站
中心广场站
妇幼医院站
终点
上车的人数
18
15
12
7
5
0
下车的人数
0
$- 3$
$- 4$
$- 10$
$- 11$

(1)、到终点下车还有人；

(2)、车行驶在哪两站之间车上的乘客最多？站到站；

(3)、若每人乘坐一站需买票1元，问该车这次出车能收入多少钱？

查看试题解析
23. 某校开展了“爱我中华”经典诵读活动，并设立了一、二、三等奖，根据需要购买了50件奖品，其中二等奖的奖品件数比一等奖奖品的件数的3倍少2件，各种奖品的单价如表所示：

一等奖奖品
二等奖奖品
三等奖奖品
单价（元/件）
20
14
8
数量（件）
x

(1)、用含x的式子表示：二等奖奖品的数量是件，三等奖奖品的数量是件；

(2)、求购买这50件奖品所需的总费用（用含x的式子表示，结果化为最简形式）；

(3)、若二等奖奖品购买了22件，则该校购买奖品共花费多少元？

查看试题解析
24. 综合探究：
整体思想是一种重要的数学思想方法，其思维方式是根据问题的结构特征，把一组数，一个代数式或几个图形视为一个整体，去观察，分析，解决问题的一种方法．这样做，不仅简化解题过程，提高思维能力，还往往可以解决按常方法解决不了的一些问题．
如：代数式 $4 (a + b) + 2 (a + b) - (a + b)$ 的化简问题．若把 $(a + b)$ 看成一个整体，
则： $4 (a + b) + 2 (a + b) - (a + b) = (4 + 2 - 1) (a + b) = 3 (a + b) = 3 a + 3 b$ ．
这就是数学解题中的“整体思想”．
请运用上面的“整体思想”解决下列问题：

(1)、尝试应用：化简 $5 (x + y)^{2} - 7 (x + y) + 2 (x + y)^{2} + 6 (x + y)$

(2)、拓展运用：如图1，点O是线段 $A B$ 上一点，C、D分别是线段 $A O 、 B O$ 的中点，当 $A B = 16$ 时，求线段 $C D$ 的长度．

(3)、迁移运用：如图2，长方形纸片 $A B C D$ ，点E ， F分别是边 $A B ， C D$ 上任意一点，连接 $E F$ ．将 $∠ B E F$ 对折，点B落在直线 $E F$ 上的点 $B^{'}$ 处，得折痕 $E M$ ；将 $∠ A E F$ 对折，点A落在直线 $E F$ 上的点 $A^{'}$ 处，得折痕 $E N$ ， $∠ N E M$ 的度数会随着折痕的变化而变化吗？说明你的理由．

查看试题解析
25. 综合应用：
三角尺是我们学习数学常见的工具，同时也因它的应用广泛性，常常作为命题的素材．
【数学来源于生活】
动手实践：将一副三角尺按甲、乙、丙、丁四种不同方式摆放．

(1)、在的摆放方式中 $∠ α$ 与 $∠ β$ 互余；在的摆放方式中 $∠ α$ 与 $∠ β$ 互补

(2)、在哪种摆放方式中 $∠ α$ 与 $∠ β$ 相等？请说明理由．

(3)、【抽象数学问题】如图1所示，将两块直角三角尺的直角顶点C叠放在一起．若 $∠ D C E = 25 °$ ，则 $∠ A C B =$ $°$ ；若 $∠ A C B = 130 °$ ，则 $∠ D C E =$ $°$ ．

(4)、如图2所示，若两个同样的三角板，将 $60 °$ 锐角的顶点A叠放在一起，则 $∠ D A B$ 与 $∠ C A E$ 有何数量关系，请说明理由．

查看试题解析

	起点	东湖广场站	朝南路站	中心广场站	妇幼医院站	终点
上车的人数	18	15	12	7	5	0
下车的人数	0	$- 3$	$- 4$	$- 10$	$- 11$

	一等奖奖品	二等奖奖品	三等奖奖品
单价（元/件）	20	14	8
数量（件）	x