广东省佛山市高明区2023-2024学年七年级上学期学期期末数学试题
试卷更新日期:2024-03-14 类型:期末考试
一、选择题,本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,请用2B铅笔把答题卡上对应题目所选的选项涂黑.
-
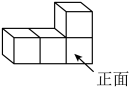
1. 四个大小相同的正方体搭成的几何体如图所示,从正面看到的视图是( )
 A、
A、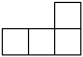 B、
B、 C、
C、 D、
D、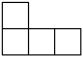 2. 下列各数中绝对值最小的数是( )A、 B、 C、7 D、03. 下列式子中,符合代数式书写格式的有( )
2. 下列各数中绝对值最小的数是( )A、 B、 C、7 D、03. 下列式子中,符合代数式书写格式的有( )① ;② ;③ ;④m+2天;⑤
A、2个 B、3个 C、4个 D、5个4. 开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为( )A、两点之间,线段最短 B、经过一点有无数条直线 C、两点确定一条直线 D、两点之间线段的长度,叫做这两点之间的距离5. 为了了解2023年某县九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩,下列说法正确的是( )A、2023年某县九年级学生是总体 B、样本容量是1000 C、1000名九年级学生是总体的一个样本 D、每一名九年级学生是个体6. 若是关于x的方程的解,则a的值为( )A、2 B、 C、4 D、7. 用一个平面去截一个三棱柱,截面边数最多为( )条A、3 B、4 C、5 D、68. 将方程式去分母,结果正确的是( )A、 B、 C、 D、9. 一副三角尺拼成如图所示的图案,则 ( ) A、 B、 C、 D、10. 把一张长方形的纸对折,如图所示可得到一条折痕,继续对折,对折时每次折痕与上次的折痕保持平行,连续对折6次后得到( )条折痕.
A、 B、 C、 D、10. 把一张长方形的纸对折,如图所示可得到一条折痕,继续对折,对折时每次折痕与上次的折痕保持平行,连续对折6次后得到( )条折痕. A、14 B、31 C、63 D、127
A、14 B、31 C、63 D、127二、填空题.本大题共6小题,每小题3分,共18分.请将下列各题的正确答案填写在答题卡相应的位置上.
-
11. 高明区皂幕山某一天早晨的气温为 , 中午上升了 , 夜间又下降了 , 则这天夜间皂幕山的气温是 .12. 点A、B在数轴上对应的数分别为和5,则线段的长度为 .13. 一次数学竞赛有25题选择题,选对一题得4分,选错或不答一题倒扣2分,小明同学做了25题,得82分.设他答对了x题,则可列方程为 .14. 已知 , 则代数式的值是 .15. 若有理数a、b互为倒数,c、d互为相反数,则 .16. 国外四个城市与北京的时差如上表,当北京时间为时,悉尼时间的时针与分针所夹角为 .
城市
时差h
纽约
悉尼
伦敦
罗马
三、解答题(一):本大题共3小题,17题12分,1819每小题7分,共26分.
-
17.(1)、计算:(2)、解方程:18. 有一种牛奶软包装盒如图1所示,为了生产这种包装盒,需要先画出展开图纸样.
 (1)、图2给出的四种纸样A、B、C、D,正确的有 .(2)、求包装盒的表面积.19. 先化简,再求值: , 其中 , .
(1)、图2给出的四种纸样A、B、C、D,正确的有 .(2)、求包装盒的表面积.19. 先化简,再求值: , 其中 , .四、解答题(二),本大题共3小题,每小题8分,共24分.
-
20. 某学校开展了“学习强国”的宣传教育活动.为了解这次活动的效果,学校从全校2700名学生中随机抽取部分学生进行趣味答题测试(测试满分100分,得分x均为不小于60的整数),并将测试成绩分为四个等级:基本合格(),合格(),良好(),优秀(),制作了如图统计图(部分信息未给出).

由图中给出的信息解答下列问题:
(1)、求测试成绩为合格的学生人数,并补全频数分布直方图.(2)、求扇形统计图中“良好”所对应的扇形圆心角的度数.(3)、如果全校学生都参加测试,请你根据抽样测试的结果,估计该校获得优秀的学生有多少人?21. 2024年1月日历排列如图所示,用“X”形的方式任意框五个数. (1)、若框住的5个数中,正中间的一个数为10,则这5个数的和为;(2)、用式子表示“X”形框内五个数的和.(3)、“X”形框能否框住这样的5个数,使得它们的和等于120?若能,求出正中间的数;若不能,请说明理由.22. 如图所示,点C在线段上, , 点M、N分别是、的中点.
(1)、若框住的5个数中,正中间的一个数为10,则这5个数的和为;(2)、用式子表示“X”形框内五个数的和.(3)、“X”形框能否框住这样的5个数,使得它们的和等于120?若能,求出正中间的数;若不能,请说明理由.22. 如图所示,点C在线段上, , 点M、N分别是、的中点. (1)、求的长度;(2)、求的长度;(3)、若数P在直线上,且 , 点Q为的中点,请直接写出的长度,不用说明理由.
(1)、求的长度;(2)、求的长度;(3)、若数P在直线上,且 , 点Q为的中点,请直接写出的长度,不用说明理由.五、解答题(三),本大题共2小题,每小题11分,共22分
-
23. 高明某电器商城某品牌电视迎“双节”活动,现进行促销,已知某款电视机进价为1800元.(1)、若按进价提高后出售,则售价元;(2)、若按标价的8折出售,仍可获利 , 求该品款电视机的标价.(3)、若现在搞“消费券”满减活动,单笔每满1000元减125元(最多可叠加使用2张),某顾客使用消费券后,仍要付现金2000元,如果要使某品牌电视在“双节”促销活动的销售额为27万元,销售量应增加多少台?24.
 (1)、①如图1所示,点O是直线上一点,平分 , 平分 , 则°;
(1)、①如图1所示,点O是直线上一点,平分 , 平分 , 则°;②如图2所示,射线在内部,且 , 平分 , 平分 , 则°;
(2)、如图3所示,射线在内部,平分 , 平分 . 根据(1)的结果,请写出你发现的结论并说明理由;(3)、若 , 射线在的外部,平分 , 平分 , 求的度数.(均指小于平角的角)