广西壮族自治区桂林市2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-03-14 类型：期末考试

进入出卷网下载

一、单选题（共12小题，每小题3分，共36分，请将答案填在答题卡上）

1. 有理数 $- \frac{1}{3}$ ， $- 2$ ， 0，1中最小的一个数是（）

A、1 B、0 C、 $- 2$ D、 $- \frac{1}{3}$

查看试题解析
2. 如果水位上升3米记作 $+ 3$ 米，那么 $- 5$ 米表示水位（）

A、上升5米 B、下降5米 C、上升2米 D、下降3米

查看试题解析
3. 如图，数轴上有A，B，C，D四个点，其中绝对值最小的数对应的点是（）

A、点A B、点B C、点C D、点D

查看试题解析
4. 下列调查中，你认为适合采用全面调查是（）

A、《新闻联播》电视栏目的收视率 B、一批灯泡的使用寿命 C、一个班级学生的体重 D、我国中小学生喜欢上数学课的人数

查看试题解析
5. 桂林以其独特的山水风光而闻名于世．这里的自然美景如诗如画，仿佛置身于一幅巨大的画卷之中，深受国内外游客的喜爱．据统计，2023年暑假期间，漓江游船和排筏累计接待游客1970000人次．将1970000用科学记数法表示为（）

A、 $1.97 \times 1 0^{6}$ B、 $19.7 \times 1 0^{5}$ C、 $1.97 \times 1 0^{7}$ D、 $1.97 \times 1 0^{5}$

查看试题解析
6. 单项式 $- \frac{2 x y^{2}}{3}$ 的次数是（）

A、 $- \frac{2}{3}$ B、1 C、2 D、3

查看试题解析
7. 如果 $2 x^{n + 2} y^{3}$ 与 $- 3 x^{3} y^{2 m - 1}$ 是同类项，那么m，n的值是（）

A、 $m = 2$ ， $n = 1$ B、 $m = 0$ ， $n = 1$ C、 $m = 2$ ， $n = 2$ D、 $m = 1$ ， $n = 2$

查看试题解析
8. 如图，点A、B在直线l上，点C是直线l外一点，可知 $C A + C B > A B$ ，其依据是（）

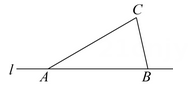A、两点之间，线段最短 B、两点确定一条直线 C、两点之间，直线最短 D、直线比线段长

查看试题解析
9. 《诗经》是中国古代诗歌的开端，最早的一部诗歌总集，共有311篇，其中6篇为笙诗，只有标题，没有内容，余下的诗篇可分为《风》、《雅》、《颂》三个部分．其中，《风》的篇数是《颂》的4倍，《雅》的篇数比《颂》的3倍少15篇．若设《颂》有 $x$ 篇，下列根据题意列出的方程正确的是（）

A、 $4 x + 3 x + 15 + x + 6 = 311$ B、 $\frac{1}{4} x + \frac{1}{3} x - 15 + x + 6 = 311$ C、 $4 x + 3 x - 15 + x + 6 = 311$ D、 $\frac{1}{4} x + \frac{1}{3} x + 15 + x + 6 = 311$

查看试题解析
10. 下面说法与所示的几何图形相符的是（）

A、点 $P$ 在直线 $n$ 上 B、直线 $O A$ 和直线 $m$ 表示同一条直线 C、点 $P$ 在射线 $O B$ 上 D、直线 $O A$ 与直线 $P B$ 都经过点 $O$

查看试题解析
11. 如图，已知直线上A，B两点相距 $12 c m$ ，点 $C$ 是线段 $A B$ 的中点，点 $D$ 在直线 $A B$ 上且与点 $B$ 相距 $8 c m$ ，则 $C D$ 的长度是（）

A、2cm B、14cm C、14cm或8cm D、14cm或2cm

查看试题解析
12. 如图是一个运算程序，若第1次输入 $a$ 的值为16，则第2024次输出的结果是（）

A、1 B、2 C、4 D、8

查看试题解析

二、填空题（共6小题，每小题2分，共12分，请将答案填在答题卡上）

13. -5的倒数是.

查看试题解析
14. 计算： $2 \times (- 3) =$ .

查看试题解析
15. 某校为了了解初一年级 $300$ 名学生每天完成作业所用时间的情况，从中对 $20$ 名学生每天完成作业所用时间进行了抽查，这个问题中的样本容量是.

查看试题解析
16. 钟表3时30分时，时针与分针所成的角的度数为．

查看试题解析
17. 若代数式 $2 a^{2} + 3 a + 1$ 的值是6，那么代数式 $6 a^{2} + 9 a + 7$ 的值是．

查看试题解析
18. 三个面积均是 $m$ 的多边形如图叠放，其中，正方形阴影部分外的面积是 $a$ ，六边形阴影部分外的面积是 $b$ ，若两块阴影部分的面积之和正好是五边形面积的一半，则a、b、m三者之间的数量关系是．

查看试题解析

三、解答题（本大题共8题，共72分，请将解答过程写在答题卡上）

19. 计算：

(1)、 $7 - (- 3) + 5$

(2)、 $- 1^{4} \times 2 \div \frac{1}{2}$ ．

查看试题解析
20. 将有理数 $- 2.5 ， 0 ， 2 \frac{1}{2} ， 2023 ， - 35 % ， 0.6$ 分别填在相应的大括号里．
整数：{ …}；
负数：{ …}；
正分数：{ …}

查看试题解析
21. 解方程：

(1)、 $7 x - (3 x - 3) = 1$ ；

(2)、 $\frac{1 - 2 x}{3} = \frac{3 x + 1}{2} - 3$ ．

查看试题解析
22. 先化简，再求值： $x y - (3 x - 2 x y) + (3 x y - 2 x)$ ，其中 $x = - 1 ， y = 2$ ．

查看试题解析
23. 2023年在杭州举办的第十九届亚运会，共有45个国家和地区的代表队、12000多名运动员参加，共颁发金牌482枚．某校新闻社团的同学根据图1金牌榜前四名的金牌数绘制了不完整的条形统计图和扇形统计图．
根据以上信息，解答下列问题：

(1)、在扇形统计图中，字母A、B所代表的国家名称分别是A：；B：；

(2)、除前四名外，其他国家和地区在第十九届亚运会上共夺得金牌多少枚？

(3)、在扇形统计图中，求中国代表队所得金牌数对应扇形的圆心角度数．（精确到 $1 °$ ）

(4)、你还能从图中得到什么信息？（写一条即可）

查看试题解析
24. 某水利工程，甲工程队单独施工需要40天可以完成，乙工程队单独施工需要60天可以完成．

(1)、现在乙工程队施工10天后，为了加快进度，甲工程队加入，两队合作完成余下的工程，问完成此项水利工程一共用了多少天？

(2)、完成此项水利工程，甲、乙二队共得到施工费68万元，如果按每队完成的工作量计算施工费，那么甲工程队可以得到多少万元？

查看试题解析
25. 综合与实践：
【问题情境】七年级（1）班的同学在劳动实践课上采挖红薯，通过对红薯的称重感受“正数与负数”在生活中的应用．
【实践探究】同学们一共挖了10筐红薯，以每筐 $30 k g$ 为标准，超过的千克数记作正数，不足的千克数记作负数，称重后记录如下：
筐号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
重量/千克
$- 3$
$2.5$
1
$- 0.5$
0
4
1
$- 1.5$
$- 2.5$
2
【问题解决】

(1)、求这10筐红薯的总重量是多少千克？

(2)、为了让更多的人分享劳动成果，该班同学每人分得2千克后，决定将剩余的红薯赠送给敬老院的爷爷奶奶们．已知敬老院共有138名老人，平均每位老人分得 $1.5$ 千克的红薯，求七年级（1）班的学生人数．

查看试题解析
26. 综合与探究
【提出问题】小明在学习中遇到这样一个问题：如图1， $∠ A O B = α （ 0 ° < α < 90 ° ）$ ，请作一个 $∠ A O C$ ，使 $∠ A O C$ 与 $∠ B O C$ 互余（ $∠ A O C > ∠ B O C$ ），即 $∠ A O C + ∠ B O C = 90 °$ ．
【动手操作】小明是这样思考的：如图2所示，若射线 $O C$ 在 $∠ A O B$ 的内部，则 $∠ A O C + ∠ B O C < 90 °$ ，所以射线 $O C$ 在 $∠ A O B$ 的外部；然后通过构造直角 $∠ A O D$ ，找到 $∠ A O C$ 的余角，如图3所示；进而分析要使 $∠ A O C$ 与 $∠ B O C$ 互余，只需 $∠ B O C = ∠ C O D$ ．
因此，小明找到了解决问题的方法：过点O作射线 $O A$ 的垂线 $O D$ ，利用量角器作出 $∠ B O D$ 的平分线 $O C$ ，这样就得到 $∠ A O C$ 与 $∠ B O C$ 互余．请你帮助小明完成下列推理说明：

(1)、已知：如图3， $∠ A O D = 90 °$ ，射线 $O C$ 平分 $∠ B O D$ ．请说明 $∠ A O C$ 与 $∠ B O C$ 互余．
解：理由：因为射线 $O C$ 平分 $∠ B O D$ （已知），
所以 $∠ B O C =$ （角平分线的定义），
由于 $∠ A O D = 90 °$ ，即 $∠ A O C + ∠ C O D =$ $°$ ，
所以 $∠ A O C + ∠ B O C = 90 °$ （），即 $∠ A O C$ 与 $∠ B O C$ 互余．

(2)、【类比操作】如图4，若 $∠ A O B = 40 °$ ，参考小明的画法，请在图4中作出一个 $∠ A O E$ ，使 $∠ A O E$ 与 $∠ B O E$ 互补（ $∠ A O E > ∠ B O E$ ），并直接写出 $∠ A O E$ 的度数．

(3)、【拓展延伸】如图5，已知 $∠ A O B = β （ 90 ° < β < 180 ° ）$ ，若 $∠ A O B$ 与 $∠ B O C$ 互补，射线 $O M$ 平分 $∠ A O B$ ，射线 $O N$ 平分 $∠ B O C$ ．请根据题意，补全图形，并求 $∠ M O N$ 的度数．

查看试题解析

筐号	①	②	③	④	⑤	⑥	⑦	⑧	⑨	⑩
重量/千克	$- 3$	$2.5$	1	$- 0.5$	0	4	1	$- 1.5$	$- 2.5$	2