广西壮族自治区南宁市2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-03-14 类型:期末考试
一、单选题
-
1. 很多学校设计校微时,会融入数学元素,下列校徽的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列式子是分式的是( )A、 B、 C、 D、3. 如图,南宁白沙大桥是一座斜拉索桥,造型美观,结构稳固,其蕴含的数学道理是( )
2. 下列式子是分式的是( )A、 B、 C、 D、3. 如图,南宁白沙大桥是一座斜拉索桥,造型美观,结构稳固,其蕴含的数学道理是( ) A、三角形的稳定性 B、四边形的不稳定性 C、三角形两边之和大于第三边 D、三角形内角和等于4. 北斗芯片的技术日趋成熟,支持北斗三号系统的(即)工艺芯片已实现规模化应用,用科学记数法表示正确的是( )A、 B、 C、 D、5. 方程的解的情况是( )A、 B、 C、 D、无解6. 如图,若 , 则的度数是( )
A、三角形的稳定性 B、四边形的不稳定性 C、三角形两边之和大于第三边 D、三角形内角和等于4. 北斗芯片的技术日趋成熟,支持北斗三号系统的(即)工艺芯片已实现规模化应用,用科学记数法表示正确的是( )A、 B、 C、 D、5. 方程的解的情况是( )A、 B、 C、 D、无解6. 如图,若 , 则的度数是( ) A、 B、 C、 D、7. 下列各式计算正确的是( )A、 B、 C、 D、8. 如图,的中线交于点 , 若阴影部分的面积是 , 则的面积是( )
A、 B、 C、 D、7. 下列各式计算正确的是( )A、 B、 C、 D、8. 如图,的中线交于点 , 若阴影部分的面积是 , 则的面积是( ) A、 B、 C、 D、9. 如图,用螺丝钉将两根小棒的中点固定,利用全等三角形知识,测得的长就是锥形瓶内径的长,其中,判定和全等的方法是( )
A、 B、 C、 D、9. 如图,用螺丝钉将两根小棒的中点固定,利用全等三角形知识,测得的长就是锥形瓶内径的长,其中,判定和全等的方法是( ) A、 B、 C、 D、10. 如图,把两个电阻串联起来,线路上的电流为 , 电压为 , 则 , 当时,的值是( )
A、 B、 C、 D、10. 如图,把两个电阻串联起来,线路上的电流为 , 电压为 , 则 , 当时,的值是( ) A、 B、 C、 D、11. 如图,在中, , 是的角平分线,若 , , 则点到的距离为( )
A、 B、 C、 D、11. 如图,在中, , 是的角平分线,若 , , 则点到的距离为( ) A、2 B、3 C、4 D、512. 八年级学生去距学校10千米的荆州博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.若设骑车学生的速度为 , 则可列方程为( )A、 B、 C、 D、
A、2 B、3 C、4 D、512. 八年级学生去距学校10千米的荆州博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.若设骑车学生的速度为 , 则可列方程为( )A、 B、 C、 D、二、填空题
-
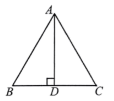
13. 若分式 有意义,则x满足.14. 如图,等边三角形中,是上的高, , 则 .
 15. 分解因式: .16. 如图,在杭州举行的第19届亚运会的奖牌取名“湖山”,以良渚文化中的礼器玉琮为表征,其外轮廓为八边形,这个八边形的内角和是度.
15. 分解因式: .16. 如图,在杭州举行的第19届亚运会的奖牌取名“湖山”,以良渚文化中的礼器玉琮为表征,其外轮廓为八边形,这个八边形的内角和是度. 17. 某农户租两块土地种植沃柑,第一块是边长为的正方形,第二块是长为 , 宽为的长方形,则第二块比第一块的面积多了 .18. 如图,在中,的垂直平分线交于点 , 交于点是直线上一点,则周长的最小值为 .
17. 某农户租两块土地种植沃柑,第一块是边长为的正方形,第二块是长为 , 宽为的长方形,则第二块比第一块的面积多了 .18. 如图,在中,的垂直平分线交于点 , 交于点是直线上一点,则周长的最小值为 .
三、解答题
-
19. 计算: .20. 先化简,再求值: , 其中 .21. 如图,已知的三个顶点的坐标分别是 , , .
 (1)、画出与关于轴对称的 , 并直接写出的坐标;(2)、在轴上有一点 , 使得 , 请直接写出点的坐标.22. 如图,点分别在上, .
(1)、画出与关于轴对称的 , 并直接写出的坐标;(2)、在轴上有一点 , 使得 , 请直接写出点的坐标.22. 如图,点分别在上, . (1)、求证:;(2)、若 , 求的度数.23. 数学家波利亚说过:“为了得到一个方程,我们必须把同一个量用两种不同的方法表示出来,即将一个量算两次,从而建立等量关系.”类似的,我们可以用两种不同的方法来表示同一个图形的面积,从而得到一个等式.
(1)、求证:;(2)、若 , 求的度数.23. 数学家波利亚说过:“为了得到一个方程,我们必须把同一个量用两种不同的方法表示出来,即将一个量算两次,从而建立等量关系.”类似的,我们可以用两种不同的方法来表示同一个图形的面积,从而得到一个等式. (1)、如图 , 大正方形是由两个小正方形和两个形状大小完全相同的长方形拼成,请用两种不同的方法表示图中大正方形的面积.
(1)、如图 , 大正方形是由两个小正方形和两个形状大小完全相同的长方形拼成,请用两种不同的方法表示图中大正方形的面积.方法:;方法:;根据以上信息,可以得到的等式是;
(2)、如图 , 大正方形是由四个边长分别为的直角三角形(为斜边)和一个小正方形拼成,请用两种不同的方法分别表示小正方形的面积,并推导得到之间的数量关系;(3)、在()的条件下,若 , 求斜边的值.24. 为提高快递包裹分拣效率,物流公司引进了快递自动分拣流水线.一条某型号的自动分拣流水线的工作效率是一名工人工作效率的倍,用这条自动分拣流水线分拣件包裹比一名工人分拣这些包裹要少用小时.(1)、这条自动分拣流水线每小时能分拣多少件包裹?(2)、新年将至,某转运中心预计每小时分拣的包裹量达件,则至少应购买多少条该型号的自动分拣流水线,才能完成分拣任务?25. 综合与实践:初步认识筝形后,实践小组动手制作了一个“筝形功能器”,如图,在筝形ABCD中,AB=AD,CB=CD.
 (1)、【操作应用】如图1,将“筝形功能器”上的点与的顶点重合,分别放置在角的两边上,并过点画射线 , 求证:是的平分线;(2)、【实践拓展】实践小组尝试使用“筝形功能器”检测教室门框是否水平.如图2,在仪器上的点处栓一条线绳,线绳另一端挂一个铅锤,仪器上的点紧贴门框上方,观察发现线绳恰好经过点 , 即判断门框是水平的.实践小组的判断对吗?请说明理由.26. 探究与证明:
(1)、【操作应用】如图1,将“筝形功能器”上的点与的顶点重合,分别放置在角的两边上,并过点画射线 , 求证:是的平分线;(2)、【实践拓展】实践小组尝试使用“筝形功能器”检测教室门框是否水平.如图2,在仪器上的点处栓一条线绳,线绳另一端挂一个铅锤,仪器上的点紧贴门框上方,观察发现线绳恰好经过点 , 即判断门框是水平的.实践小组的判断对吗?请说明理由.26. 探究与证明:我们知道,在一个三角形中,相等的边所对的角相等.那么,不相等的边所对的角之间的大小关系是怎样呢?
 (1)、【观察猜想】如图 , 在中, , 猜想与的大小关系;(2)、【操作证明】如图 , 将折叠,使边落在上,点落在上的点,折线交于点 , 连接 , 发现,由 , 可得 , , 请证明()中所猜想的结论;(3)、【类比探究】如图 , 在中, , 小邕同学运用类似的操作进行探究:将折叠,使点与点重合,折线交于点 , 交于点 , 连接 , 请证明: .
(1)、【观察猜想】如图 , 在中, , 猜想与的大小关系;(2)、【操作证明】如图 , 将折叠,使边落在上,点落在上的点,折线交于点 , 连接 , 发现,由 , 可得 , , 请证明()中所猜想的结论;(3)、【类比探究】如图 , 在中, , 小邕同学运用类似的操作进行探究:将折叠,使点与点重合,折线交于点 , 交于点 , 连接 , 请证明: .