贵州省贵阳市数学2023-2024学年高三上学期一轮模拟卷

试卷更新日期：2024-03-14 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {- 1 ， 0 ， 1 ， 2 ， 3 ， 4} ， B = {x ∣ x < 3}$ ，则 $A ∩ B =$ （）

A、 ${- 1 ， 0 ， 1 ， 2}$ B、 ${- 1 ， 0 ， 1}$ C、 ${0 ， 1 ， 2}$ D、 ${x ∣ x < 3}$

查看试题解析
2. 已知 $s i n α = \frac{4}{5}$ ， $α \in (0 ， \frac{π}{2})$ ，则 $s i n (α - \frac{π}{4}) =$ （）

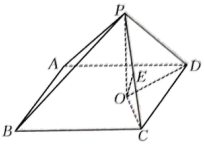
A、 $\frac{\sqrt{2}}{10}$ B、 $- \frac{\sqrt{2}}{10}$ C、 $\frac{7 \sqrt{2}}{10}$ D、 $- \frac{7 \sqrt{2}}{10}$

查看试题解析
3. 若无穷等差数列 ${a_{n}}$ 的公差为 $d$ ，则“ $d > 0$ ”是“ $\exists k \in N^{*}$ ， $a_{k} > 0$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 实数 $a ， b ， c$ 满足 $\sqrt[3]{c} - \sqrt[3]{b} = 1 ， a = c + l o g_{5} (x^{2} - x + 3) (x \in R)$ ，则 $a ， b ， c$ 的大小关系是（）

A、 $a > b > c$ B、 $b > c > a$ C、 $c > b > a$ D、 $a > c > b$

查看试题解析
5. 在平行四边形ABCD中， $A B = 3 \sqrt{2} ， A D = 2 ， \vec{A E} = \vec{E B} ， ∠ B A D = \frac{π}{4}$ ，则 $\vec{A C} \cdot \vec{D E} =$ （）

A、2 B、 $2 \sqrt{2}$ C、 $2 \sqrt{3}$ D、4

查看试题解析
6. 设A，B为两个事件，已知 $P (A) = 0.5$ ， $P (B) = 0.3$ ， $P (B | \bar{A}) = 0.2$ ，则 $P (B | A) =$ （）

A、0.3 B、0.4 C、0.5 D、0.6

查看试题解析
7. 如图，已知圆柱的斜截面是一个椭圆，该椭圆的长轴AC为圆柱的轴截面对角线，短轴长等于圆柱的底面直径.将圆柱侧面沿母线AB展开，则椭圆曲线在展开图中恰好为一个周期的正弦曲线.若该段正弦曲线是函数 $y = 2 s i n ω x (ω > 0)$ 图像的一部分，且其对应的椭圆曲线的离心率为 $\frac{1}{2}$ ，则 $ω$ 的值为（）

A、 $\frac{\sqrt{3}}{6}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\sqrt{3}$ D、2

查看试题解析
8. 设体积相等的正方体、正四面体和球的表面积分别为 $S_{1} ， S_{2} ， S_{3}$ ，则（）

A、 $S ₁ < S ₂ < S ₃$ B、 $S ₂ < S ₁ < S ₃$ C、 $S ₃ < S ₁ < S ₂$ D、 $S ₃ < S ₂ < S ₁$

查看试题解析

二、多选题

9. 若a ， $b \in R$ ，则下列命题正确的是（）

A、若 $a b \neq 0$ 且 $a < b$ ，则 $\frac{1}{a} > \frac{1}{b}$ B、若 $a < b$ ，则 $a^{3} < b^{3}$ C、若 $a > b > 0$ ，则 $\frac{b + 1}{a + 1} < \frac{b}{a}$ D、若 $a | a | < b | b |$ ，则 $a < b$

查看试题解析
10. 某食品的保鲜时间y（单位：小时）与储藏温度x（单位：℃）满足函数关系 $y = e^{k x + b}$ （ $e = 2.718 \cdot \cdot \cdot$ 为自然对数的底数，k，b为常数）.若该食品在0℃的保鲜时间是192小时，在14℃的保鲜时间是48小时，则下列说法正确的是（）
参考数据： $2 . 8^{5} \approx 172$ ， $2 . 7^{6} \approx 387$

A、 $b \in (5 ， 6)$ B、若该食品储藏温度是21℃，则它的保鲜时间是16小时 C、 $k < 0$ D、若该食品保鲜时间超过96小时，则它的储藏温度不高于7℃

查看试题解析
11. 欧拉函数 $φ (n)$ （ $n \in N^{*}$ ）的函数值等于所有不超过正整数n ，且与n互质的正整数的个数（公约数只有1的两个正整数称为互质整数），例如： $φ (3) = 2$ ， $φ (4) = 2$ ，则（）

A、 $φ (4) \cdot φ (6) = φ (8)$ B、当n为奇数时， $φ (n) = n - 1$ C、数列 ${φ (2^{n})}$ 为等比数列 D、数列 ${\frac{φ (2^{n})}{φ (3^{n})}}$ 的前n项和小于 $\frac{3}{2}$

查看试题解析
12. 如图，在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，已知M ， N ， P分别是棱 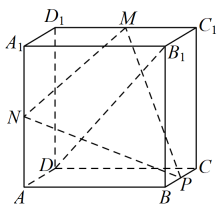$C_{1} D_{1}$ ， $A A_{1}$ ， $B C$ 的中点，Q为平面 $P M N$ 上的动点，且直线 $Q B_{1}$ 与直线 $D B_{1}$ 的夹角为 $30 °$ ，则（）

A、 $D B_{1} ⊥$ 平面 $P M N$ B、平面 $P M N$ 截正方体所得的截面面积为 $3 \sqrt{3}$ C、点Q的轨迹长度为 $π$ D、能放入由平面PMN分割该正方体所成的两个空间几何体内部（厚度忽略不计）的球的半径的最大值为 $\frac{3 - \sqrt{3}}{2}$

查看试题解析

三、填空题

13. ${(2 x^{2} + x - y)}^{5}$ 的展开式中 $x^{5} y^{2}$ 的系数为（用数字作答）.

查看试题解析
14. 某市统计高中生身体素质的状况，规定身体素质指标值不小于60就认为身体素质合格．现从全市随机抽取 100名高中生的身体素质指标值 $x_{i} (i = 1 ， 2 ， 3 ， ⋯ ， 100)$ ，经计算 $\sum_{i = 1}^{100} x_{i} = 7200$ ， $\sum_{i = 1}^{100} x_{i}^{2} = 100 \times (7 2^{2} + 36)$ ．若该市高中生的身体素质指标值服从正态分布 $N (μ ， σ^{2})$ ，则估计该市高中生身体素质的合格率为．（用百分数作答，精确到0.1%）
参考数据：若随机变量X服从正态分布 $N (μ ， σ^{2})$ ，则 $P (μ - σ \leq X \leq μ + σ) \approx 0.6827$ ， $P (μ - 2 σ \leq X \leq μ + 2 σ) \approx 0.9545$ ， $P (μ - 3 σ \leq X \leq μ + 3 σ) \approx 0.9973$ ．

查看试题解析
15. 已知函数 $f (x) = e^{2 x} - 2 a (x - 2) e^{x} - a^{2} x^{2} (a > 0)$ 恰有两个零点，则 $a =$ .

查看试题解析
16. 在 $1 ， 2 ， ⋯ ， 50$ 中随机选取三个数，能构成公差不小于5的等差数列的概率为．

查看试题解析

四、解答题

17. 已知数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n}$ 满足 $2 S_{n} + a_{n} - 1 = 0$ .

(1)、求 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = l o g_{27} a_{n}$ ，求数列 ${\frac{1}{b_{n} b_{n + 1}}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
18. 已知某公司生产的风干牛肉干是按包销售的，每包牛肉干的质量 $M$ （单位：g）服从正态分布 $N (250 ， σ^{2})$ ，且 $P (M < 248) = 0.1$ .

(1)、若从公司销售的牛肉干中随机选取3包，求这3包中恰有2包质量不小于 $248 g$ 的概率；

(2)、若从公司销售的牛肉干中随机选取 $K$ （ $K$ 为正整数）包，记质量在 $248 g ~ 252 g$ 内的包数为 $X$ ，且 $D (X) > 320$ ，求 $K$ 的最小值.

查看试题解析
19. 在 $△ A B C$ 中，内角A ， B ， C的对边分别为a ， b ， c ， $a = 3 \sqrt{2}$ ， $a s i n B = b s i n (A + \frac{π}{3})$ .

(1)、求角A；

(2)、作角A的平分线与 $B C$ 交于点 $D$ ，且 $A D = \sqrt{3}$ ，求 $b + c$ .

查看试题解析
20. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为矩形， $P O ⊥$ 平面 $A B C D$ ，垂足为 $O$ ， $E$ 为 $P C$ 的中点， $O E / /$ 平面 $P A D$ ．

(1)、证明： $P C = P D$ ；

(2)、若 $A D = 2 A B = 4$ ， $O C ⊥ O D$ ， $P C$ 与平面 $A B C D$ 所成的角为60°，求平面 $P B C$ 与平面 $P C D$ 夹角的余弦值．

查看试题解析
21. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的离心率为 $\frac{\sqrt{42}}{6}$ ，且其焦点到渐近线的距离为1.

(1)、求 $C$ 的方程；

(2)、若动直线 $l$ 与 $C$ 恰有1个公共点，且与 $C$ 的两条渐近线分别交于 $P ， Q$ 两点， $O$ 为坐标原点，证明： $△ O P Q$ 的面积为定值.

查看试题解析
22. 已知函数 $f (x) = \frac{l n x + a}{x}$ ， $x \in [1 ， + \infty)$ .

(1)、讨论 $f (x)$ 的单调性.

(2)、是否存在两个正整数 $x_{1}$ ， $x_{2}$ ，使得当 $x_{1} > x_{2}$ 时， ${(x_{1} - x_{2})}^{x_{1} x_{2}} = x_{1}^{x_{2}} x_{2}^{x_{1}}$ ？若存在，求出所有满足条件的 $x_{1}$ ， $x_{2}$ 的值；若不存在，请说明理由.

查看试题解析