四川省泸州市马街中学2023-2024学年高三下学期数学开学试卷
试卷更新日期:2024-03-14 类型:开学考试
一、单选题:本题共12小题,每小题5分,共60分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 设全集 , 集合 , 集合 , 则( )A、 B、 C、 D、2. 如果一个复数的实部与虚部相等,则称这个复数为“等部复数”,若复数为“等部复数”,则实数的值为( )A、 B、 C、 D、3. 某学校高一年级有名学生,现采用系统抽样方法,从中抽取人作问卷调查,将人按、、、、随机编号,则抽取的人中,编号落入区间的人数为( )A、 B、 C、 D、4. 已知正三角形边长为2,用斜二测画法画出该三角形的直观图,则所得直观图的面积为( )A、 B、 C、 D、5. 已知 , 则圆与直线的位置关系是( )A、相切 B、相交 C、相离 D、不确定6. 如图,在矩形中, , 过点向所在区域等可能任作一条射线 , 已知事件“射线与线段有公共点”发生的概率为 , 则边的长为( )
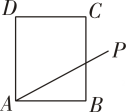 A、 B、 C、 D、7. 已知等差数列满足 , 则中一定为零的项是( )A、 B、 C、 D、8. 三棱柱中,为棱的中点,若 , , , 则( )
A、 B、 C、 D、7. 已知等差数列满足 , 则中一定为零的项是( )A、 B、 C、 D、8. 三棱柱中,为棱的中点,若 , , , 则( ) A、 B、 C、 D、9. 已知 , , 且 , 均为锐角,则的值为( )A、 B、 C、或 D、10. 千年宝地,一马当先年月日时分,吉利银河宝鸡马拉松赛在宝鸡市行政中心广场鸣枪开跑,比赛吸引了全国各地职业选手及路跑爱好者共万人的热情参与为确保活动顺利举行,组委会自起点开始大约每隔公里设置一个饮水站志愿者为选手递送饮料或饮用水,为选手提供能量补给 , 两个饮水站中间设置一个用水站志愿者为选手递送湿毛巾等,协助医务工作者 , 共个饮用水服务点,分别由含甲、乙在内的支志愿者服务队负责,则甲队和乙队服务类型不同且服务点不相邻的概率为( )A、 B、 C、 D、11. 已知椭圆 , , , 过点的直线与椭圆交于 , , 过点的直线与椭圆交于 , , 且满足 , 设和的中点分别为 , , 若四边形为矩形,且面积为 , 则该椭圆的离心率为( )A、 B、 C、 D、12. 已知函数 , 若是函数的唯一极值点,则实数的取值范围是
A、 B、 C、 D、9. 已知 , , 且 , 均为锐角,则的值为( )A、 B、 C、或 D、10. 千年宝地,一马当先年月日时分,吉利银河宝鸡马拉松赛在宝鸡市行政中心广场鸣枪开跑,比赛吸引了全国各地职业选手及路跑爱好者共万人的热情参与为确保活动顺利举行,组委会自起点开始大约每隔公里设置一个饮水站志愿者为选手递送饮料或饮用水,为选手提供能量补给 , 两个饮水站中间设置一个用水站志愿者为选手递送湿毛巾等,协助医务工作者 , 共个饮用水服务点,分别由含甲、乙在内的支志愿者服务队负责,则甲队和乙队服务类型不同且服务点不相邻的概率为( )A、 B、 C、 D、11. 已知椭圆 , , , 过点的直线与椭圆交于 , , 过点的直线与椭圆交于 , , 且满足 , 设和的中点分别为 , , 若四边形为矩形,且面积为 , 则该椭圆的离心率为( )A、 B、 C、 D、12. 已知函数 , 若是函数的唯一极值点,则实数的取值范围是( )
A、 B、 C、 D、二、填空题:本题共4小题,每小题5分,共20分。
-
13. 设 , 满足约束条件 , 则的最大值为 .14. 等比数列中, , , 则 .15. 若正数、满足 , 则的最小值为 .16. 已知双曲线的左顶点为 , 右焦点为 , 离心率为 , 动点在双曲线的右支上且不与右顶点重合,若恒成立,则双曲线的渐近线方程为 .
三、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
-
17. 在中,、、分别是角、、所对的边,已知在 , , , 且 .(1)、求角大小;(2)、若面积为 , , 求的长.18. 如图,在棱长为的正方体中,是的中点,是的中点,
 (1)、求证:平面;(2)、求平面与平面夹角的余弦值.19. 椭圆:的离心率为 , 右顶点为 , 设点为坐标原点,点为椭圆上异于左、右顶点的动点,面积的最大值为 .(1)、求椭圆的标准方程;(2)、设直线:交轴于点 , 其中 , 直线交椭圆于另一点 , 直线和分别交直线于点和 , 若 , , , 四点共圆,求的值.
(1)、求证:平面;(2)、求平面与平面夹角的余弦值.19. 椭圆:的离心率为 , 右顶点为 , 设点为坐标原点,点为椭圆上异于左、右顶点的动点,面积的最大值为 .(1)、求椭圆的标准方程;(2)、设直线:交轴于点 , 其中 , 直线交椭圆于另一点 , 直线和分别交直线于点和 , 若 , , , 四点共圆,求的值.