福建省漳州市2024届高三毕业班第三次质量检测数学试题
试卷更新日期:2024-03-14 类型:高考模拟
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知集合 , 则( )A、 B、 C、 D、2. ( )A、65 B、160 C、165 D、2103. 若复数 , 则( )A、 B、2 C、 D、4. 已知 , 则( )A、 B、 C、 D、5. 一个圆台的上、下底面的半径分别为1和4,体积为 , 则它的表面积为( )A、 B、 C、 D、6. 在中,是边上一点,且是的中点,记 , 则( )A、 B、 C、 D、7. 已知函数的定义域均为是奇函数,且的图象关于对称, , 则( )A、4 B、8 C、 D、8. 将数列与的公共项从小到大排列得到数列 , 则( )A、 B、 C、 D、
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得3分,有选错的得0分.
-
9. 已知函数的部分图像如图所示,则下列说法正确的是( )
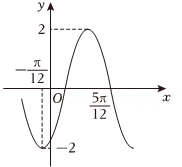 A、的图象关于中心对称 B、在区间上单调递增 C、在上有4个零点,则实数的取值范围是 D、将的图象向右平移个单位长度,可以得到函数的图象10. 点在抛物线上,为其焦点,是圆上一点, , 则下列说法正确的是( )A、的最小值为 B、周长的最小值为 C、当最大时,直线的方程为 D、过作圆的切线,切点分别为 , 则当四边形的面积最小时,的横坐标是111. 如图,在棱长为4的正方体中,分别是棱的中点,为底面上的动点,则下列说法正确的是( )
A、的图象关于中心对称 B、在区间上单调递增 C、在上有4个零点,则实数的取值范围是 D、将的图象向右平移个单位长度,可以得到函数的图象10. 点在抛物线上,为其焦点,是圆上一点, , 则下列说法正确的是( )A、的最小值为 B、周长的最小值为 C、当最大时,直线的方程为 D、过作圆的切线,切点分别为 , 则当四边形的面积最小时,的横坐标是111. 如图,在棱长为4的正方体中,分别是棱的中点,为底面上的动点,则下列说法正确的是( )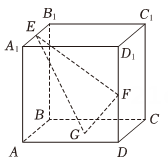 A、当为的中点时, B、若在线段上运动,三棱锥的体积为定值 C、存在点 , 使得平面截正方体所得的截面面积为 D、当为的中点时,三棱锥的外接球表面积为
A、当为的中点时, B、若在线段上运动,三棱锥的体积为定值 C、存在点 , 使得平面截正方体所得的截面面积为 D、当为的中点时,三棱锥的外接球表面积为三、填空题:本题共3小题,每小题5分,共15分.
-
12. 曲线在处的切线方程为 .13. 点分别为双曲线的左、右焦点,过作斜率为的直线与双曲线的左、右两支分别交于两点,若为以为底的等腰三角形,则的离心率为 .14. 如图,某城市有一条公路从正西方向通过路口后转向西北方向 , 围绕道路打造了一个半径为的扇形景区,现要修一条与扇形景区相切的观光道 , 则的最小值为 .

四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
-
15. 如图,在四棱锥中,底面 .
 (1)、求证:平面;(2)、求平面与平面的夹角的余弦值.16. 已知数列满足, .(1)、求数列的通项公式;(2)、若对任意 , 求的最小整数值.17. 已知函数 .(1)、讨论的单调性;(2)、若不等式恒成立,求的取值范围;(3)、当时,试判断函数的零点个数,并给出证明.18. 已知椭圆的右焦点为是上的点,直线的斜率为 .(1)、求的方程;(2)、过点作两条相互垂直的直线分别交于两点和两点,的中点分别记为 , 且为垂足.试判断是否存在点 , 使得为定值?若存在,请求出点的坐标;若不存在,请说明理由.19. “绿色出行,低碳环保”的理念已经深入人心,逐渐成为新的时尚.甲、乙、丙三人为响应“绿色出行,低碳环保”号召,他们计划每天选择“共享单车”或“地铁”两种出行方式中的一种.他们之间的出行互不影响,其中,甲每天选择“共享单车”的概率为 , 乙每天选择“共享单车”的概率为 , 丙在每月第一天选择“共享单车”的概率为 , 从第二天起,若前一天选择“共享单车”,后一天继续选择“共享单车”的概率为 , 若前一天选择“地铁”,后一天继续选择“地铁”的概率为 , 如此往复.(1)、若3月1日有两人选择“共享单车”出行,求丙选择“共享单车”的概率;(2)、记甲、乙、丙三人中3月1日选择“共享单车”出行的人数为 , 求的分布列与数学期望;(3)、求丙在3月份第天选择“共享单车”的概率 , 并帮丙确定在3月份中选择“共享单车”的概率大于“地铁”的概率的天数.
(1)、求证:平面;(2)、求平面与平面的夹角的余弦值.16. 已知数列满足, .(1)、求数列的通项公式;(2)、若对任意 , 求的最小整数值.17. 已知函数 .(1)、讨论的单调性;(2)、若不等式恒成立,求的取值范围;(3)、当时,试判断函数的零点个数,并给出证明.18. 已知椭圆的右焦点为是上的点,直线的斜率为 .(1)、求的方程;(2)、过点作两条相互垂直的直线分别交于两点和两点,的中点分别记为 , 且为垂足.试判断是否存在点 , 使得为定值?若存在,请求出点的坐标;若不存在,请说明理由.19. “绿色出行,低碳环保”的理念已经深入人心,逐渐成为新的时尚.甲、乙、丙三人为响应“绿色出行,低碳环保”号召,他们计划每天选择“共享单车”或“地铁”两种出行方式中的一种.他们之间的出行互不影响,其中,甲每天选择“共享单车”的概率为 , 乙每天选择“共享单车”的概率为 , 丙在每月第一天选择“共享单车”的概率为 , 从第二天起,若前一天选择“共享单车”,后一天继续选择“共享单车”的概率为 , 若前一天选择“地铁”,后一天继续选择“地铁”的概率为 , 如此往复.(1)、若3月1日有两人选择“共享单车”出行,求丙选择“共享单车”的概率;(2)、记甲、乙、丙三人中3月1日选择“共享单车”出行的人数为 , 求的分布列与数学期望;(3)、求丙在3月份第天选择“共享单车”的概率 , 并帮丙确定在3月份中选择“共享单车”的概率大于“地铁”的概率的天数.