贵州省黔南州2023-2024学年多校联考八年级上学期期末数学试卷

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、选择题（以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，每小题3分，共30分）

1. 单板滑雪大跳台是北京冬奥会比赛项目之一，下面的比赛项目图标组成的四个图形中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段能首尾相接构成三角形的是（　　）

A、2.5cm ， 3.5cm ， 7cm B、2.9cm ， 4.1cm ， 5cm C、4cm ， 5cm ， 10cm D、2cm ， 4cm ， 6cm

查看试题解析
3. 式子（﹣ab）⁴•a²化简后的结果是（　　）

A、a²b⁴ B、a⁶b⁴ C、a⁸b⁴ D、a¹⁶b⁴

查看试题解析
4. 下列等式中，从左到右的变形是因式分解的是（　　）

A、a（a﹣3）＝a²﹣3a B、（a+1）²＝a²+2a+1 C、 $a + 2 = a (1 + \frac{2}{a})$ D、a²﹣9＝（a+3）（a﹣3）

查看试题解析
5. 计算 $\frac{x - 2}{x - 1} \cdot \frac{x - 1}{(2 - x)^{2}}$ 的结果是（　　）

A、 $\frac{1}{x - 2}$ B、 $- \frac{1}{2}$ C、 $\frac{1}{2 - x}$ D、x

查看试题解析
6. 如图，点B在AE上，∠CBE＝∠DBE ，要通过“ASA”判定△ABC≌△ABD ，可补充的一个条件是（　　）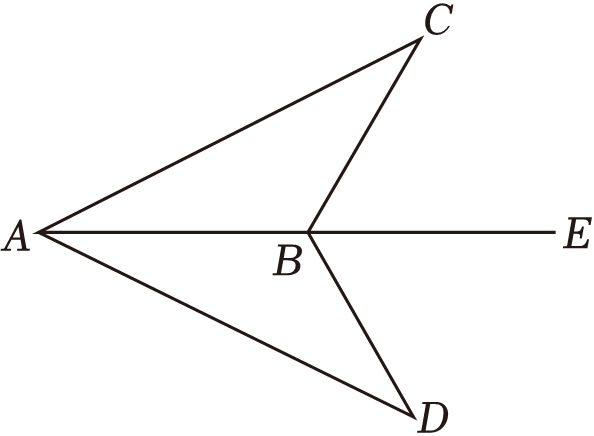

A、∠CAB＝∠DAB B、∠ACB＝∠ADB C、AC＝AD D、BC＝BD

查看试题解析
7. 下面计算正确的是（　　）

A、（a+1）²＝a²+1 B、（a²）³﹣a⁸÷a⁴＝a⁴ C、（m²n）³•m²n＝m⁸n⁴ D、（12a²b²c﹣4a²b）÷4a²b＝3bc

查看试题解析
8. 如图，△ABC中，AB的垂直平分线DE交AC于点D ，垂足为E ，连接BD ．如果△DBC的周长等于10cm ， BC＝4cm ，那么AC的长是（　　）

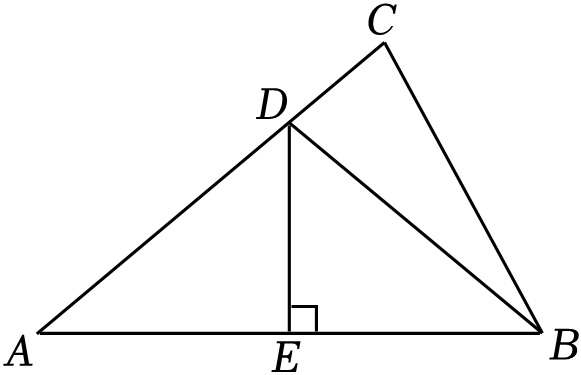A、5cm B、6cm C、7cm D、9cm

查看试题解析
9. 若x²﹣nx+36是关于x的完全平方式，则n的值为（　　）

A、6 B、12 C、±12 D、36

查看试题解析
10. 某校曾开展了“喜迎二十大，争做好少年”的数学知识应用能力竞赛活动，活动中小明同学用两把完全相同的直尺就作出一个角的平分线．如图，将一把直尺的边与射线OA重合，另一把直尺的边与射线OB重合，两把直尺的另一边在角的内部交于点P ，作射线OP ，小明说：“射线OP就是∠AOB的角平分线．”他这样做的依据是（　　）

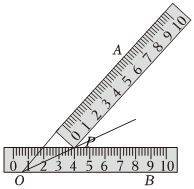A、在角的内部，到角的两边距离相等的点在这个角的平分线上 B、角平分线上的点到这个角的两边的距离相等 C、三角形的三条高交于三点 D、三角形三边的垂直平分线交于一点

查看试题解析

二、填空题（每小题3分，共12分）

11. 禁令标志是交通标志中的一种，是对车辆加以禁止或限制的标志，如禁止通行、禁止停车、禁止左转弯、禁止鸣喇叭、限制速度、限制重量等．如图，该禁令标志的内角和是．

查看试题解析
12. 计算：（ $\frac{1}{3}$ ）^﹣1+|π﹣3.14|⁰＝．

查看试题解析
13. 已知：x²﹣y²＝2023，且x﹣y＝2023，则x+y＝．

查看试题解析
14. 如图，∠MAN的边AM上有一点B ，且AB＝10，点C是边AN上一动点，∠MBC与∠NCB的角平分线交于点O ，当∠BOC＝75°时，BC的最小值是．

查看试题解析

三、解答题（本大题7小题，共58分）

15.

(1)、因式分解：4a²（x﹣y）﹣9（x﹣y）；

(2)、先化简： $\frac{a + 1}{a - 3} - \frac{3 - a}{a + 2} \div \frac{a^{2} - 6 a + 9}{a^{2} - 4}$ ，再从1、2、3、﹣1、﹣2中选一个合适的数代入求值．

查看试题解析
16. 如图，AB＝CD ， AM⊥BC于点M ， DN⊥BC于点N ， CM＝BN ，连接AN ， DM ．
求证：

(1)、△ABM≌△DCN；

(2)、AN∥DM ．

查看试题解析
17. 如图，在△ABC中，AB＝AC ， ∠BAC＝45°，AD和BE是高，它们相交于点F ．
求证：

(1)、△AEF≌△BEC；

(2)、AF＝2CD ．

查看试题解析
18. 如图，平面直角坐标系内有一个△ABC ，点A、B、C的坐标分别是（﹣5，1）、（﹣2，2）、（﹣2，5）．

(1)、请作出△ABC关于x轴的对称图形△A₁B₁C₁；

(2)、x轴上有一点M ，且MA＝MB ，请你用尺规作图的方法找出点M（保留作图痕迹不写作法）；

(3)、在y轴上求作一点N ，使点N到M ， C两点的距离之和最小，请作出点N（保留作图痕迹不写作法）．

查看试题解析
19. 新冠疫情结束后，2023年贵州省旅游迎来了大发展，榕江“村超”、从江“村BA”、贵阳“路边音乐会”等更是助力“多彩贵州”火爆全网．每逢比赛日，高速路出口车流量激增．现有甲、乙两个高速路出口，甲高速路出口每小时驶出车辆是乙高速路出口的1.2倍，甲高速路出口驶出600辆车比乙高速路出口驶出400辆车的时间多1小时，甲、乙两个高速路出口每小时各驶出多少辆车？

查看试题解析
20. 观察图形，结合材料解决问题：

(1)、如图①，将几个边长不等的小正方形和小长方形拼成一个大正方形．
①用下列两种不同的方法计算这个大正方形的面积：
方法一：（整体法）用大正方形的边长的平方表示：．
方法二：（局部法）用3个小正方形与6个小长方形的面积和表示：．
②若a、b、c三个数满足a²+b²+c²＝20，ab+bc+ca＝16，则（a+b+c）²＝．

(2)、如图②，将边长为a的小正方形AEFG和边长为b的大正方形ABCD拼在一起，且D ， A ， E三点在同一直线上，连接DB和DF ，若两个正方形的边长满足a+b＝8，ab＝12，请求出阴影部分的面积．

查看试题解析
21. 八年级学生芳芳放学后去幼儿园接弟弟回家，姐弟俩双手相牵在幼儿园门口开心地旋转起来．芳芳突然想起某天数学活动课上老师提出的一个问题：如图，在△AOB和△EOF中，OA＝OB ， OE＝OF ，且∠1＝∠2，连接AE ， BF交于点M ．试猜想AE与BF的数量关系，并加以证明．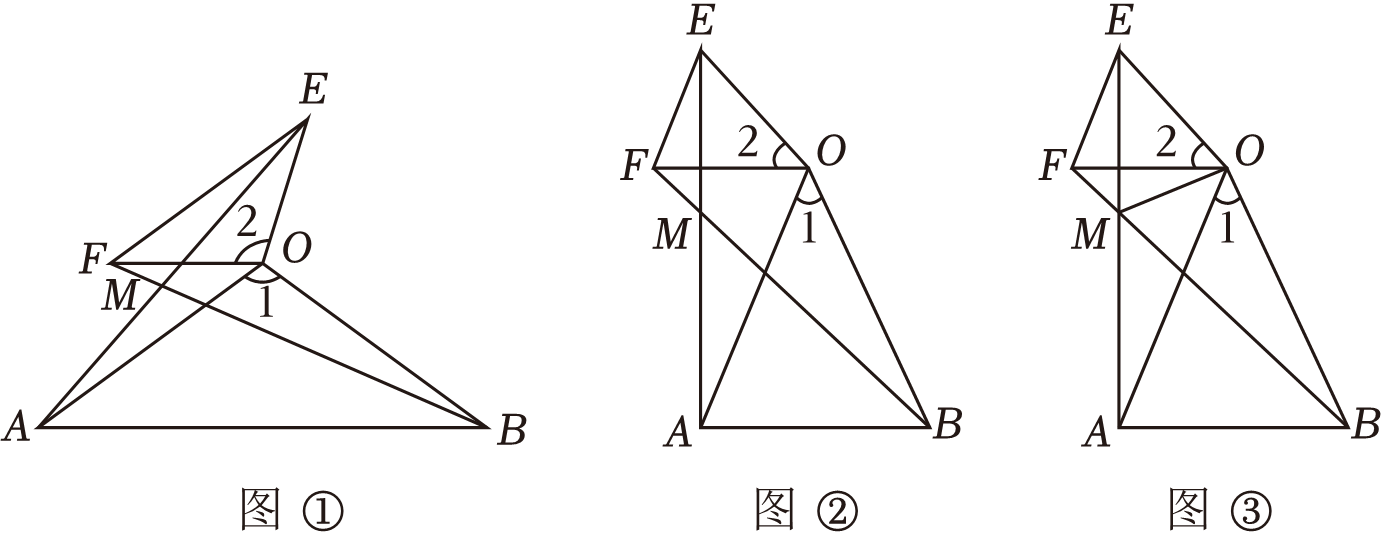

(1)、独立思考：如图①，请解决老师提出的问题。

(2)、实践探究：如图②．当∠1＝45°时，∠AMB＝度；当∠OAB＝65°时，∠AMB＝度；

(3)、解决问题：如图③，连接OM ， MO平分∠BME吗？并加以说明．

查看试题解析