贵州省黔南布依族苗族自治州2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，每小题2分，共24分．在每小题所给的四个选项中，有且只有一项是符合题目要求的）

1. 方程 $x^{2} - 4 = 0$ 的解为（）

A、 $x = 2$ B、 $x_{1} = - 4 ， x_{2} = 4$ C、 $x_{1} = - 2 ， x_{2} = 2$ D、 $x = 4$

查看试题解析
2. 下列有关环保的四个标志中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 某电视台举行歌手大赛，每场比赛都有10道综合素质测试题供选手随机抽取作答，编号为1~10．在某场比赛中，前两位选手已经分别抽走了2号、7号题，第3位选手抽中8号题的概率是（）

A、 $\frac{1}{7}$ B、 $\frac{1}{8}$ C、 $\frac{1}{9}$ D、 $\frac{1}{10}$

查看试题解析
4. 如图，在方格纸中，将 $△ A O B$ 绕点 $O$ 按顺时针方向旋转 $90 °$ 后得到 $△ A^{'} O B^{'}$ ，则下列四个图形中正确的是（）

A、 B、 C、 D、

查看试题解析
5. 如图， $P A ， P B$ 与 $⊙ O$ 分别相切于点 $A ， B ， P A = 2 ， ∠ P = 60 °$ ，则 $A B =$ （）

A、3 B、2 C、6 D、4

查看试题解析
6. 如图， $A B$ 是 $⊙ O$ 的弦， $A C$ 切 $⊙ O$ 于点 $A ， B C$ 经过圆心 $O$ ．若 $∠ B = 25 °$ ．则 $∠ C =$ （）

A、65° B、60° C、50° D、40°

查看试题解析
7. 如图， $A B$ 是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点 $E$ ．若 $A B = 10 ， C D = 8$ ，则 $A E$ 的长为（）

A、3 B、6 C、8 D、9

查看试题解析
8. 将抛物线 $y = 3 x^{2} + 2$ 先向左平移2个单位长度，再向下平移3个单位长度，则得到的抛物线的解析式为（）

A、 $y = 3 (x - 2)^{2} - 1$ B、 $y = 3 (x - 2)^{2} + 5$ C、 $y = 3 (x + 2)^{2} - 1$ D、 $y = 3 (x + 2)^{2} + 5$

查看试题解析
9. 习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气．”某校积极开展全民阅读活动，打造书香校园，在各班建立图书角．据统计，九（10）班第一周参与阅读128人次，阅读人次每周递增，到第三周累计参与阅读608人次．若阅读人次的周平均增长率为x ，则可得方程（）

A、 $128 (1 + x) = 608$ B、 $128 (1 + x)^{2} = 608$ C、 $128 (1 + x) + 128 (1 + x)^{2} = 608$ D、 $128 + 128 (1 + x) + 128 (1 + x)^{2} = 608$

查看试题解析
10. 在同一平面直角坐标系中，函数 $y = a x + a$ 和 $y = - a x^{2} + 2 x + 2 (a$ 是常数，且 $a \neq 0)$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
11. 如图，把半径为3的⊙O沿弦AB，AC折叠，使 $\overset{⌢}{A B}$ 和 $\overset{⌢}{A C}$ 都经过圆心O，则阴影部分的面积为（）．

A、 $π$ B、 $2 π$ C、 $3 π$ D、 $4 π$

查看试题解析
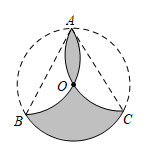12. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，下列结论：① $a b c < 0$ ；② $2 a + b = 0$ ；③ $4 a + 2 b + c > 0$ ；④ $a m^{2} + b m < a + b (m \neq 1)$ ；⑤ $3 a + c < 0$ ，其中正确结论的个数是（）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题（本大题共4小题，每小题3分，共12分）

13. 在平面直角坐标系中，点 $P$ 关于原点对称的点 $Q$ 的坐标是 $(- 2 ， 3)$ ，则点 $P$ 的坐标是．

查看试题解析
14. 抛物线 $y = x^{2} - 7 x + 6$ 与 $x$ 轴的两个交点之间的距离为．

查看试题解析
15. 如图，开关 $K_{1} ， K_{2}$ 和 $K_{3}$ 处于断开状态，随机闭合开关 $K_{1} ， K_{2}$ 和 $K_{3}$ 中的两个，两盏灯同时发光的概率为．

查看试题解析
16. 如图，在平面直角坐标系中，点 $A ， B$ 的坐标分别为 $(1 ， 0) ， (1 ， \sqrt{3})$ ，将 $△ O A B$ 绕原点 $O$ 顺时针旋转60°，再将其各边都扩大为原来的2倍，使得 $O A_{1} = 2 O A ， O B_{1} = 2 O B$ ，得到 $△ O A_{1} B_{1}$ ，将 $△ O A_{1} B_{1}$ 绕原点 $O$ 顺时针旋转 $60 °$ ，再将其各边都扩大为原来的2倍，使得 $O A_{2} = 2 O A_{1}$ ， $O B_{2} = 2 O B_{1}$ ，得到 $△ O A_{2} B_{2} ， \cdot \cdot \cdot$ ，如此继续下去，得到 $△ O A_{2022} B_{2022}$ ，则点 $A_{2022}$ 的坐标是．

查看试题解析

三、解答题（本大题共9小题，共64分．解答时应写出必要的文字说明、证明过程或演算步骤）

17. 用适当的方法解下列方程；

(1)、 $x^{2} - 6 x + 8 = 0$ ；

(2)、 $3 x (x + 3) = 2 (x + 3)$ ．

查看试题解析
18. 如图，在正方形网格中，每个小正方形的边长都是1个单位长度，在平面直角坐标系内， $△ A B O$ 的三个顶点的坐标分别为 $A (- 1 ， 3) ， B (- 4 ， 3) ， O (0 ， 0)$ ．

(1)、画出 $△ A B O$ 绕点 $O$ 顺时针旋转90°后得到的 $△ A_{1} B_{1} O$ ，并写出点 $B_{1}$ 的坐标；

(2)、在（1）的条件下，求点 $B$ 旋转到点 $B_{1}$ 所经过的路径长（结果保留 $π$ ）．

查看试题解析
19. 2023年5月30日上午，神舟十六号载人飞船成功发射，举国振奋．为了使同学们进一步了解中国航天科技的快速发展，黔南州某中学九（1）班团支部在文体艺术节期间组织了一场手抄报比赛．要求该班每位同学从A：北斗卫星；B：5G时代：C：东风快递；D：智轨快运四个主题中任选一个自己喜欢的主题．比赛结束后，该班团支部对同学们所选主题进行统计，绘制成如下两种不完整的统计图，请根据统计图中的信息解答下列问题．

(1)、九（1）班共有_▲_名学生；补全折线统计图．

(2)、李刚和王丽从A，B，C，D四个主题中各任选一个主题，请用列表或画树状图的方法求出他们选择相同主题的概率．

查看试题解析
20. 阅读材料：
解方程： ${(x^{2} - 1)}^{2} - 5 (x^{2} - 1) + 4 = 0$ ．我们可以将 $x^{2} - 1$ 视为一个整体，然后设 $x^{2} - 1 = y$ ，则 ${(x^{2} - 1)}^{2} = y^{2}$ ，原方程化为 $y^{2} - 5 y + 4 = 0$ ①，解得 $y_{1} = 1 ， y_{2} = 4$ ．
当 $y = 1$ 时， $x^{2} - 1 = 1 ， ∴ x^{2} = 2 ， ∴ x = \pm \sqrt{2}$ ．
当 $y = 4$ 时， $x^{2} - 1 = 4 ， ∴ x^{2} = 5 ， ∴ x = \pm \sqrt{5}$ ．
$∴$ 原方程的解为 $x_{1} = \sqrt{2} ， x_{2} = - \sqrt{2} ， x_{3} = \sqrt{5} ， x_{4} = - \sqrt{5}$ ．
根据上面的解答，解决下面的问题：

(1)、填空：在由原方程得到方程①的过程中，利用法达到降次的目的，体现了的数学思想；

(2)、解方程； $x^{4} - x^{2} - 12 = 0$ ．

查看试题解析
21. 如图，点M，N分别在正方形ABCD的边BC，CD上，且∠MAN＝45°.把△ADN绕点A顺时针旋转90°得到△ABE.

(1)、求证：△AEM≌△ANM.

(2)、若BM＝3，DN＝2，求正方形ABCD的边长.

查看试题解析
22. 已知 $x_{1}, x_{2}$ 是关于 $x$ 的一元二次方程 $x^{2} - 2 (m + 1) x + m^{2} + 5 = 0$ 的两个实数根.

(1)、求m的取值范围；

(2)、若 $(x_{1} - 1) (x_{2} - 1) = 28$ ，求 $m$ 的值；

查看试题解析
23. 为了振兴乡村经济，增加村民收入，某村委会干部带领村民把一片坡地改造后种植了优质葡萄，今年正式上市销售，并在网上直播推销优质葡萄．在销售的30天中，第一天卖出20千克，为了扩大销量，采取了降价措施，以后每天比前一天多卖出4千克．第 $x$ 天的售价为y元/千克，y关于x的函数解析式为 $y = {\begin{array}{l} m x - 76 m (1 \leq x < 20 ， x 为正整数) ， \\ n (20 \leq x \leq 30 ， x 为正整数) ， \end{array}$ 且第12天的售价为32元/千克，第26天的售价为25元/千克．已知种植销售葡萄的成本是18元/千克，每天的利润是 $W$ 元．

(1)、 $m =$ ， $n =$ ；

(2)、销售优质葡萄第几天时，当天的利润最大？最大利润是多少？

查看试题解析
24. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，以 $A C$ 为直径的 $⊙ O$ 交 $A B$ 于点 $E ， D$ 是 $B C$ 上一点，连接 $D E$ ，且 $∠ B = ∠ B E D$ ．

(1)、求证： $E D$ 是 $⊙ O$ 的切线；

(2)、若 $B E = 16 ， E D = 10$ ，求 $A C$ 的长．

查看试题解析
25. 如图，抛物线 $y = a x^{2} + b x - 4 (a \neq 0)$ 与 $x$ 轴交于点 $A (- 2 ， 0)$ 和点 $B (4 ， 0)$ ，与 $y$ 轴交于点 $C$ ，连接 $B C$ ．点 $P$ 是线段 $B C$ 下方抛物线上的一个动点（不与点 $B ， C$ 重合），过点 $P$ 作 $y$ 轴的平行线交 $B C$ 于点 $M$ ，交 $x$ 轴于点 $N$ ．

(1)、求该抛物线的解析式．

(2)、过点 $C$ 作 $C H ⊥ P N$ 于点 $H$ ，且 $B N = 3 C H$ ．
①求点 $P$ 的坐标．
②连接 $C P$ ，在 $y$ 轴上是否存在点 $Q$ ，使得 $△ C P Q$ 为直角三角形？若存在，求出点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析