四川省成都市龙泉驿区2023-2024学年八年级上学期期末数学试卷

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、选择题（共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）

1. 9的算术平方根是（）

A、 $3$ B、 $- 3$ C、 $\pm 3$ D、 $\pm \sqrt{3}$

查看试题解析
2. 在平面直角坐标系中，点 $A (3 ， 2)$ 关于原点对称的点的坐标是 $($ $)$

A、 $(- 3 ， 2)$ B、 $(3 ， - 2)$ C、 $(- 2 ， - 3)$ D、 $(- 3 ， - 2)$

查看试题解析
3. 下列计算正确的是 $($ $)$

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $5 \sqrt{3} - 3 \sqrt{3} = 2 \sqrt{3}$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{5}$ D、 $\sqrt{6} \div \sqrt{3} = 2$

查看试题解析
4. 下列各组数为勾股数的是 $($ $)$

A、6，12，13 B、5，12，13 C、8，15，16 D、3，4，7

查看试题解析
5. 为响应“双减”政策，进一步落实“立德树人、五育并举”的思想主张，深圳某学校积极推进学生综合素质评价改革，小芳在本学期德、智、体、美、劳的评价得分如图所示，其各项的得分分别为9，8，10，8，7，则该同学这五项评价得分的众数，中位数，平均数分别为（）

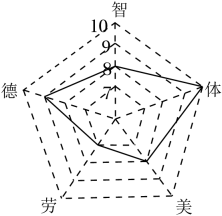A、8，8，8 B、7，8，7.8 C、8，8，8.7 D、8，8，8.4

查看试题解析
6. 《九章算术》中记载了这样一个数学问题：今有甲发长安，五日至齐；乙发齐，七日至长安．今乙发已先二日，甲仍发长安．问：几何日相逢？译文：甲从长安出发，5日到齐国；乙从齐国出发，7日到长安．现乙先出发2日，甲才从长安出发．问：多久后甲、乙相逢？设甲出发 $x$ 日，乙出发 $y$ 日后甲、乙相逢，则所列方程组正确的是 $($ $)$

A、 ${\begin{array}{l} x - 2 = y \\ \frac{1}{7} x + \frac{1}{5} y = 1 \end{array}$ B、 ${\begin{array}{l} x + 2 = y \\ \frac{1}{7} x + \frac{1}{5} y = 1 \end{array}$ C、 ${\begin{array}{l} x - 2 = y \\ \frac{1}{5} x + \frac{1}{7} y = 1 \end{array}$ D、 ${\begin{array}{l} x + 2 = y \\ \frac{1}{5} x + \frac{1}{7} y = 1 \end{array}$

查看试题解析
7. 已知点 $(- 1 ， y_{1})$ ， $(3 ， y_{2})$ 在一次函数 $y = 3 x - 1$ 的图象上，则 $y_{1}$ ， $y_{2}$ 的大小关系是 $($ $)$

A、 $y_{1} < y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} > y_{2}$ D、不能确定

查看试题解析
8. 关于一次函数 $y = \frac{1}{2} x + 2$ ，下列结论正确的是（　　）

A、图象不经过第二象限 B、图象与x轴的交点是（0，2） C、将一次函数 $y = \frac{1}{2} x + 2$ 的图象向上平移1个单位长度后，所得图象的函数表达式为 $y = \frac{1}{2} x + 3$ D、点（x₁ ， y₁）和（x₂ ， y₂）在一次函数 $y = \frac{1}{2} x + 2$ 的图象上，若x₁＜x₂ ，则y₁＞y₂

查看试题解析

二、填空题（共5个小题，每小题4分，共20分，答案写在答题卡上）

9. 比较大小： $- \sqrt{17}$ $- 4$ ．（填“ $>$ ”，“ $<$ ”或“ $=$ ” $)$

查看试题解析
10. 若 $x > 3$ ，化简二次根式 $\sqrt{x^{2} - 6 x + 9} =$ ．

查看试题解析
11. 在某次赛制为“12进4”且当场公布分数的舞蹈比赛中，小华所在的队伍当第10支队伍分数公布后仍排名第二而欢呼，请问她们判定自己已进入下一轮比赛的依据与（从平均数、众数、中位数、方差中选择）有关．

查看试题解析
12. 已知一次函数y＝kx+4（k≠0）和y＝﹣3x+b的图象交于点A（﹣3，2），则关于x ， y的二元一次方程组 ${\begin{array}{l} y = k x + 4 \\ y = - 3 x + b \end{array}$ 的解是，

查看试题解析
13. 如图，在 $Δ A B C$ 中，按以下步骤作图：①以点 $C$ 为圆心，任意长为半径作弧，分别交 $A C$ ， $B C$ 于点 $D$ 和 $E$ ；②分别以点 $D$ ， $E$ 为圆心，以大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧相交于点 $F$ ；③作射线 $C F$ 交 $A B$ 于点 $H$ ；④过点 $H$ 作 $G H / / B C$ 交 $A C$ 于点 $G$ ，若 $∠ B C H = 40 °$ ，则 $∠ C G H$ 的度数是．

查看试题解析

三、解答题（共6个小题，共48分，解答过程写在答题卡上）

14.

(1)、计算： $\sqrt{8} + | 2 - \sqrt{2} | - (π + 2024)^{0}$ ；

(2)、计算： $(\sqrt{5} - 2) (\sqrt{5} + 2) - (\sqrt{3} - 1)^{2}$ ．

查看试题解析
15.

(1)、解方程组： ${\begin{array}{l} 3 x - 2 y = 7 \\ x + 2 y = 5 \end{array}$ ；

(2)、解方程组： ${\begin{array}{l} x - \frac{y}{2} = 2 \\ 2 x + 3 y = 12 \end{array}$ ．

查看试题解析
16. 如图， $D E ⊥ A C$ ， $∠ A G F = ∠ A B C$ ， $∠ B F G = 35 °$ ， $∠ E D B = 145 °$ ．

(1)、试判断 $B F$ 与 $A C$ 的位置关系，并说明理由；

(2)、若 $G F = G B$ ，求 $∠ A$ 的度数．

查看试题解析
17. 漏刻是中国古代的一种计时工具．中国最早的漏刻出现在夏朝时期，在宋朝时期，中国漏刻的发展达到了巅峰，其精确度和稳定性得到了极大的提高．漏刻的工作原理是利用均匀水流导致的水位变化来显示时间．水从上面漏壶源源不断地补充给下面的漏壶，再均匀地流入最下方的箭壶，使得壶中有刻度的小棍匀速升高，从而取得比较精确的时刻．某学习小组复制了一个漏刻模型，研究中发现小棍露出的部分 $y$ （厘米）是时间 $x$ （分钟）的一次函数，且当时间 $x = 0$ 分钟时， $y = 2$ 厘米．表中是小明记录的部分数据，其中有一个 $y$ 的值记录错误．
$x$ （分钟）
$\dots$
10
20
30
40
$y$ （厘米）
$\dots$
2.6
3.2
3.6
4.4

(1)、你认为 $y$ 的值记录错误的数据是；

(2)、利用正确的数据确定函数表达式；

(3)、当小棍露出部分为8厘米时，对应的时间为多少？

查看试题解析
18. 如图，在平面直角坐标系中，直线 $y = 3 x + 6$ 与 $x$ 轴， $y$ 轴分别交于点 $A$ ， $C$ ，经过点 $C$ 的直线与 $x$ 轴交于点 $B$ ， $∠ C B O = 45 °$ ．

(1)、求直线 $B C$ 的解析式；

(2)、点 $G$ 是线段 $B C$ 上一动点，若直线 $A G$ 把 $Δ A B C$ 的面积分成 $1 ： 2$ 的两部分，请求点 $G$ 的坐标；

(3)、已知 $D$ 为 $A C$ 的中点，点 $P$ 是 $x$ 轴上一点，当 $Δ B D P$ 是等腰三角形时，求出点 $P$ 的坐标．

查看试题解析

四、填空题（共5个小题，每小题4分，共20分，答案写在答题卡上）

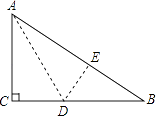
19. 若一次函数 $y = 3 x - 7$ 的图象过点 $(m ， n)$ ，则 $n - 3 m + 2 =$ ．

查看试题解析
20. 如图，有一块直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿着直线AD折叠，使它落在斜边AB上，且与AE重合，则CD的长为 cm．

查看试题解析
21. 剪纸是各种民俗活动的重要组成部分，很多剪纸作品体现了数学中的对称美．如图，蝴蝶剪纸是一幅轴对称图形，将其放在平面直角坐标系中，其中点 $E$ 坐标是 $(- 2 ， 3)$ ，现将图形进行变换，第一次关于 $y$ 轴对称，第二次关于 $x$ 轴对称，第三次关于 $y$ 轴对称，第四次关于 $x$ 轴对称，以此类推 $\dots$ ，则经过第2023次变换后点 $E$ 的对应点的坐标为．

查看试题解析
22. 若关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} 4 x - y = 5 \\ a x + b y = 2 \end{array}$ 和 ${\begin{array}{l} 3 x + y = 9 \\ b x + a y = 8 \end{array}$ 的解相同，则 $a + b =$ ．

查看试题解析
23. 如图，在 $Δ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ， $D$ 为 $Δ A B C$ 外一点，连接 $A D$ ， $B D$ ， $C D$ ，发现 $A D = 4$ ， $C D = 2$ 且 $∠ A D C = 45 °$ ，则 $B D =$ ．

查看试题解析

五、解答题（共3个小题，共30分，解答过程写在答题卡上）

24. 随着新能源电动车的逐渐普及，人们在购车时经常会面临一个问题：应该选择传统燃油车还是新能源电动车呢？某校的项目式学习小组开展了《选电动车还是燃油车呢？》的研究，发现用车费用包含购车费用和耗能费用，其中A型电动车每百公里耗电15度电，每度电0.6元，B型燃油车每百公里耗油8L ，每升油8块钱．

(1)、根据提供的信息，填写下列表格：

购车费用（万元）
每公里耗能费用（元）
A型电动车
13.5
▲
B型燃油车
8
▲

(2)、分别求出A型电动车y₁（万元），B型燃油车用车费用y₂（万元）与行驶公里数x（万公里）之间的函数关系式；在同一坐标系中画出y₁ ， y₂的草图并给出你的选择结论；

(3)、小明爸爸计划购买一辆A型电动车进行网约车工作，相关法律规定网约车限制经营年限为8年或行驶公里数不超过60万公里．于是项目组同学继续调查：网约车每年平均行程10万公里，A型电动车每年还需要保险费5000元，每1万公里保养费120元．请你帮小明爸爸计算购买A型电动车进行网约车工作共需投入多少费用．

查看试题解析
25.

【基础模型】：如图，等腰直角三角形 $A B C$ 中 $∠ A C B = 90 °$ ， $C B = C A$ ，直线 $E D$ 经过点 $C$ ，过点 $A$ 作 $A D ⊥ E D$ 于点 $D$ ，过点 $B$ 作 $B E ⊥ E D$ 于点 $E$ ，易证明 $Δ B E C ≅ Δ C D A$ ，我们将这个模型称为“ $K$ 形图”．

(1)、【模型应用】：
如图1所示，已知 $B (0 ， 3)$ ， $C (2 ， 0)$ ，连接 $B C$ ，以 $B C$ 为直角边，点 $C$ 为直角顶点作等腰直角三角形 $A B C$ ，点 $A$ 在第一象限，则点 $A$ 的坐标为；

(2)、【模型构建】：
如图2，在平面直角坐标系中，直线 $y = 2 x + 4$ 与 $x$ 轴， $y$ 轴分别交于点 $A$ ， $B$ ， $B C ⊥ A B$ 交 $x$ 轴于点 $C$ ．
①请求出直线 $B C$ 的函数解析式；
② $P$ 为 $x$ 轴上一点，连接 $B P$ ，若 $∠ A B P = 45 °$ ，求 $P$ 坐标．

查看试题解析
26. 在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ，点 $D$ 为边 $A B$ 上的动点，连接 $C D$ ，将 $Δ A C D$ 沿直线 $C D$ 翻折，得到对应的△ $A^{'} C D$ ， $C A^{'}$ 与 $A B$ 所在的直线交于点 $E$ ．

(1)、如图1，当 $A^{'} D ⊥ A D$ 时，求证： $C E = C B$ ；

(2)、若 $∠ A = 30 °$ ， $B C = 2$ ．
①如图2，当 $E$ 与 $B$ 重合时，求 $A D$ 的长；
②连接 $A^{'} B$ ，当△ $A^{'} B D$ 是以 $B D$ 为直角边的直角三角形时，求 $A D$ 的长．

查看试题解析

$x$ （分钟）	$\dots$	10	20	30	40
$y$ （厘米）	$\dots$	2.6	3.2	3.6	4.4

	购车费用（万元）	每公里耗能费用（元）
A型电动车	13.5	▲
B型燃油车	8	▲