云南省昆明市五华区2023-2024学年九年级上学期期末数学试卷

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、单选题（共12小题，每小题3分，共36分）

1. 在北京冬奥会举办之前，北京冬奥会组委曾面向全球征集 $2022$ 年冬奥会会徽和冬残奥会会徽设计方案，共收到设计方案 $4506$ 件，以下是部分参选作品，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列方程中，是一元二次方程的是（　　）

A、x﹣9＝0 B、x²+6x+5＝0 C、y＝x²﹣1 D、x²﹣2x﹣3

查看试题解析
3. 二次函数y=﹣（x﹣1）²+3的图象的顶点坐标是（　　）

A、（﹣1，3） B、（1，3） C、（﹣1，﹣3） D、（1，﹣3）

查看试题解析
4. 下列说法正确的是（　　）

A、“随意翻到一本书的某页，页码是奇数”是必然事件 B、“画一个三角形，其内角和一定等于180°”是必然事件 C、“二氧化碳能使澄清石灰水变浑浊”是不可能事件 D、“短跑运动员1秒跑完100米”是随机事件

查看试题解析
5. 一元二次方程x²﹣4x+4=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
6. 以下生活现象中，属于旋转变换得是（　　）

A、钟表的指针和钟摆的运动 B、站在电梯上的人的运动 C、坐在火车上睡觉 D、地下水位线逐年下降

查看试题解析
7. 把抛物线y＝2x²﹣1先向右平移1个单位，再向下平移2个单位，得到的抛物线的解析式为（　　）

A、y＝2（x+1）²﹣3 B、y＝2（x+1）²+1 C、y＝2（x﹣1）²+1 D、y＝2（x﹣1）²﹣3

查看试题解析
8. AB是⊙O的直径，点C在圆上，∠ABC=65°，那么∠OCA的度数是（）

A、25° B、35° C、15° D、20°

查看试题解析
9. 一个半径为2cm的圆的内接正六边形的面积是（　　）

A、24cm² B、6 $\sqrt{3}$ cm² C、12 $\sqrt{3}$ cm² D、8 $\sqrt{3}$ cm²

查看试题解析
10. 如图，AB是⊙O的直径， $\hat{B C}$ = $\hat{C D}$ = $\hat{D E}$ ，∠COD=34°，则∠AEO的度数是（）

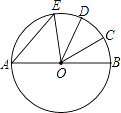A、51° B、56° C、68° D、78°

查看试题解析
11. 如图，P是⊙O外一点，射线PA、PB分别切⊙O于点A、点B ， CD切⊙O于点E ，分别交PA、PB于点D、点C ，若PB＝4，则△PCD的周长（）

A、4 B、6 C、8 D、10

查看试题解析
12. 组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比赛组织者应邀请x个队参赛，则x满足的关系式为（）

A、x（x+1）＝28 B、 $\frac{1}{2}$ x（x﹣1）＝28 C、x（x﹣1）＝28 D、 $\frac{1}{2}$ x（x+1）＝28

查看试题解析

二、填空题（每小题2分，共8分）

13. 若点A（﹣3，4）关于原点对称的点是点B ，则点B的坐标为．

查看试题解析
14. 如图， $A B$ 是 $⊙ O$ 的弦， $O C ⊥ A B$ 于点 $D$ ，交 $⊙ O$ 于点 $C$ ，若 $A B = 8$ ， $O D = 3$ ，那么 $⊙ O$ 的半径为．

查看试题解析
15. 关于x的一元二次方程x²+x﹣a＝0的一个根是1，则另一个根是．

查看试题解析
16. 要制作一个高为8cm，底面圆直径是12cm的圆锥形小漏斗，若不计接缝，不计损耗，则她所需纸板的面积是cm² ．

查看试题解析

三、解答题（共8题，56分）

17. 解方程：

(1)、3（x﹣2）²＝27；

(2)、x²+2x﹣3＝0．

查看试题解析
18. 如图，△ABC三个顶点的坐标分别为A（2，4），B（1，1），C（4，3）．

(1)、请画出△ABC关于原点成中心对称的△A₁B₁C₁；

(2)、请画出△ABC绕点B顺时针旋转90°后的△A₂B₂C₂ ，并写出点A₂的坐标；

(3)、求出（2）中C点旋转到C₂点所经过的路径长．（结果保留根号和π）．

查看试题解析
19. 某种品牌的手机经过7、8月份连续两次降价，每部售价由2500元降到了1600元.若每次下降的百分率相同，请解答：

(1)、求每次下降的百分率；

(2)、若9月份继续保持相同的百分率降价，则这种品牌的手机售价为多少元？

查看试题解析
20. 如图，四边形OABC是平行四边形，AB＝1，以点O为圆心，OC长为半径的⊙O与AB相切于点B ，与AO相交于点D ．求图中阴影部分的面积．

查看试题解析
21. 一个盒中有4个完全相同的小球，把它们分别标号为1，2，3，4，随机摸取一个小球然后放回，再随机摸出一个小球．

(1)、请用列表法（或画树状图法）列出所有可能的结果；

(2)、求两次取出的小球标号相同的概率；

(3)、求两次取出的小球标号的和大于6的概率．

查看试题解析
22. 如图，⊙O是△ABC的外接圆，AC是⊙O的直径，点D是 $\hat{A C}$ 的中点，点E是AB延长线上的一点，连接CE ， ∠E＝∠ADB ．

(1)、求证：CE是⊙O的切线，

(2)、若∠ADB＝60°，AD＝4 $\sqrt{2}$ ，求BC的长．

查看试题解析
23. 在“母亲节”期间，某校部分团员参加社会公益活动，准备用每个6元的价格购进一批许愿瓶进行销售，并将所得利润捐给慈善机构．根据市场调查，这种许愿瓶一段时间内的销售量y（个）与销售单价x（元/个）之间的关系式为：y＝﹣30x+600．

(1)、按照上述市场调查的销售规律，写出销售利润w（元）与销售单价x（元/个）之间的函数解析式；

(2)、为了方便顾客，售价定为多少时可获利1200元；

(3)、若要想获得最大利润，试确定此时的销售单价，并求出此时的最大利润．

查看试题解析
24. 如图，抛物线y＝﹣ $\frac{1}{2}$ x²+mx+n与x轴交于A、B两点，与y轴交于点C ，抛物线的对称轴交x轴于点D ，已知A（﹣1，0），C（0，2）．

(1)、求抛物线的表达式；

(2)、求△BDC的面积；

(3)、线段BC上有一动点P ，过点P作y轴的平行线，交抛物线于点Q ，求线段PQ的最大值．

查看试题解析