云南省昆明市五华区2023-2024学年七年级上学期期末数学试卷
试卷更新日期:2024-03-13 类型:期末考试
一、选择题:本题共15小题,每小题2分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. -4的绝对值是( )A、 B、 C、4 D、-42. 从正面、左面、上面观察某个立体图形,得到如图所示的平面图形,那么这个立体图形是( )
 A、
A、 B、
B、 C、
C、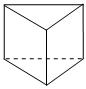 D、
D、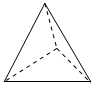 3. 中国共产党第二十次全国代表大会指出:我国经济实力实现历史性跃升,十年间中国人均国内生产总值从元增加到元数据用科学记数法可表示为( )A、 B、 C、 D、4. 单项式与是同类项,则常数的值为( )A、 B、 C、 D、5. 实数 , 在数轴上对应的点的位置如图所示,下列结论中正确的是( )
3. 中国共产党第二十次全国代表大会指出:我国经济实力实现历史性跃升,十年间中国人均国内生产总值从元增加到元数据用科学记数法可表示为( )A、 B、 C、 D、4. 单项式与是同类项,则常数的值为( )A、 B、 C、 D、5. 实数 , 在数轴上对应的点的位置如图所示,下列结论中正确的是( )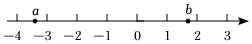 A、 B、 C、 D、6. 如果关于的方程的解是 , 那么的值是( )A、 B、 C、 D、7. 如图,某海域有三个小岛 , , , 在小岛处观测到小岛在它的北偏东的方向上,观测到小岛在它的南偏西的方向上,则的度数是( )
A、 B、 C、 D、6. 如果关于的方程的解是 , 那么的值是( )A、 B、 C、 D、7. 如图,某海域有三个小岛 , , , 在小岛处观测到小岛在它的北偏东的方向上,观测到小岛在它的南偏西的方向上,则的度数是( )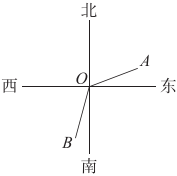 A、 B、 C、 D、8. 已知 , 则下列等式中不成立的是( )A、 B、 C、 D、9. 下列说法中,正确的是( )A、射线和射线是同一条射线 B、如果 , 那么是线段的中点 C、如果两个角互补,那么它们的角平分线所在直线的夹角为 D、如果两个角是同一个角的补角,那么它们相等10. 九章算术是人类科学史上应用数学的“算经之首”,书中记载:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?意思是:现有几个人共买一件物品,每人出钱多出钱;每人出钱,还差钱.问:人数、物价各是多少?若设物价是钱,根据题意列一元一次方程,正确的是( )
A、 B、 C、 D、8. 已知 , 则下列等式中不成立的是( )A、 B、 C、 D、9. 下列说法中,正确的是( )A、射线和射线是同一条射线 B、如果 , 那么是线段的中点 C、如果两个角互补,那么它们的角平分线所在直线的夹角为 D、如果两个角是同一个角的补角,那么它们相等10. 九章算术是人类科学史上应用数学的“算经之首”,书中记载:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?意思是:现有几个人共买一件物品,每人出钱多出钱;每人出钱,还差钱.问:人数、物价各是多少?若设物价是钱,根据题意列一元一次方程,正确的是( ) A、 B、 C、 D、11. 下列是嘉淇同学解一元一次方程的过程 .
A、 B、 C、 D、11. 下列是嘉淇同学解一元一次方程的过程 .解:去分母,得 , 第一步
去括号,得 , 第二步
移项,得 , 第三步
合并同类项,得 , 第四步
系数化为 , 得 .
上述解法中,开始出现错误的是( )
A、第一步 B、第二步 C、第三步 D、第四步12. 在 , , , . , , 中,负分数有( )A、个 B、个 C、个 D、个13. 将转化为度分秒的形式为( )A、 B、 C、 D、14. 若 , 则的值为( )A、 B、 C、 D、15. 一个由若干奇数排成的数阵,用如图所示的框去框住四个数,并求出它们的和移动这个框,框住四个数的和可能是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共4小题,每小题2分,共8分。
-
16. 用四舍五入法把3.1415926精确到0.01,所得到的近似数为 .17. 如图, , 是线段的三等分点,是线段的中点,若 , 则 .
 18. 如图图中长度单位: , 阴影部分的面积是 .
18. 如图图中长度单位: , 阴影部分的面积是 . 19. 电影哈利波特中,哈利波特穿越墙进入“站台”的镜头如示意图的站台 , 构思精妙,给观众留下深刻的印象若、站台分别位于 , 处,点位于点、之间且 , 则站台用类似电影的方法可称为 站台.
19. 电影哈利波特中,哈利波特穿越墙进入“站台”的镜头如示意图的站台 , 构思精妙,给观众留下深刻的印象若、站台分别位于 , 处,点位于点、之间且 , 则站台用类似电影的方法可称为 站台.
三、解答题:本题共8小题,共62分。解答应写出文字说明,证明过程或演算步骤。
-
20.(1)、计算:;(2)、计算:;(3)、解方程: .21. 先化简,再求值: , 其中 .22. 根据题意,补全解题过程:
如图,已知射线 , , 在内部,平分 , 平分若 , , 求的度数.

解:平分 ,
.
,
.
, ,
.
平分 ,
.
23. 饺子是中国传统食物,用一张小圆形面皮包馅制作而成,形如半月或元宝;馅饼也是非常流行的一种美食,用一张大圆形面皮包陷制作而成,呈扁圆形元旦当天,小盛和爸爸、妈妈一起制作美味的饺子和馅饼,小盛向爸爸学习制作圆形面皮,一共制作了大、小两种圆形面皮共张,爸爸和妈妈一起包饺子和馅饼,正好用完所有制作的大小面皮,小盛发现饺子的数量比馅饼数量的倍多个请你根据以上信息,求出所包饺子和馅饼各多少个?列方程解答24. 如图,已知三点 , , , 作直线 .(1)、用语句表述图中点与直线的关系: ; (2)、用直尺和圆规完成以下作图保留作图痕迹:
(2)、用直尺和圆规完成以下作图保留作图痕迹:连接 , 在线段的延长线上作线段 , 使;
(3)、连接 , 比较线段与线段的长短,并将下面的推理补充完整:, ,
,
▲ , ▲ 填推理的依据
▲ .
25. 某商户每日要购进千克小龙虾,下表是该商户记录的本周小龙虾进价的浮动情况:星期
一
二
三
四
五
六
日
价格元千克
注:正号表示价格比前一天上涨,负号表示价格比前一天下降.
已知小龙虾上周日的进价为每千克元,这周四的进价为每千克元.
(1)、求的值和本周内购进小龙虾的最高单价;(2)、商户周五将当天购进的小龙虾以每千克元全部售出,且出售时小龙虾有的损耗,求该商户在本周星期五当天的收益.26. 用、两种型号的机器生产相同的产品,产品装入同样规格的包装箱后运往仓库已知每台型机器比型机器一天多生产件产品,台型机器一天生产的产品恰好能装满箱,台型机器一天生产的产品恰好能装满箱每台型机器一天生产多少件产品?每箱装多少件产品?下面是解决该问题的两种思路,请选择其中一种思路,进行解答不需要填空
思路一:
若设每台型机器一天生产件产品,则每台型机器一天生产件产品,台型机器一天共生产 ▲ 件产品,台型机器一天共生产 ▲ 件产品,再根据相等关系: ▲ , 就可以列出方程解决问题.
思路二:
若设每箱装件产品,则台型机器一天共生产 ▲ 件产品,台型机器一天共生产 ▲ 件产品,再根据相等关系: ▲ , 就可以列出方程解决问题.
27. 如图,点 , , 是同一直线上互不重合的三个点,在线段 , , 中,若有一条线段的长度恰好是另一条线段长度的一半,则称 , , 三点存在“半分关系”. (1)、当点是线段的中点时, , , 三点 “半分关系”填“存在”或“不存在”;(2)、已知 , 点在线段上,若 , , 三点存在“半分关系”,求线段的长度;(3)、已知点 , , 是数轴上互不重合的三个点,点为原点,点表示的数是是负数 , 且 , , 三点存在“半分关系”,直接写出点表示的数的最大值与最小值的差用含的式子表示 .
(1)、当点是线段的中点时, , , 三点 “半分关系”填“存在”或“不存在”;(2)、已知 , 点在线段上,若 , , 三点存在“半分关系”,求线段的长度;(3)、已知点 , , 是数轴上互不重合的三个点,点为原点,点表示的数是是负数 , 且 , , 三点存在“半分关系”,直接写出点表示的数的最大值与最小值的差用含的式子表示 .