湖南省常德市澧县2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、选择题（共8小题，每小题3分，满分24分）

1. 下列函数不是反比例函数的是（）

A、 $y = 3 x^{- 1}$ B、 $x y = 5$ C、 $y = - \frac{x}{3}$ D、 $y = \frac{1}{2 x}$

查看试题解析
2. 平面直角坐标系 $x O y$ 中，若点 $A (x_{1} ， 2)$ 和 $B (x_{2} ， 4)$ 在反比例函数 $y = \frac{k}{x} (k > 0)$ 图像上，则下列关系式正确的是（）

A、 $x_{1} > x_{2} > 0$ B、 $x_{2} > x_{1} > 0$ C、 $x_{1} < x_{2} < 0$ D、 $x_{2} < x_{1} < 0$

查看试题解析
3. 某园林公司从外地购进某种树苗，为了解该种树苗的移植成活率，现对购进的第一批树苗进行随机抽样并统计，结果如图所示．
若该公司第二批还需种植成活2700棵该种树苗，根据统计结果，则第二批树苗购买量较为合理的是（）

A、2430棵 B、2700棵 C、3000棵 D、3140棵

查看试题解析
4. 在平面直角坐标系中，将抛物线 $y = x^{2} - 4$ 先向右平移2个单位，再向上平移2个单位，得到的抛物线的解析式是（）

A、 $y = {(x + 2)}^{2} + 2$ B、 $y = {(x - 2)}^{2} - 2$ C、 $y = {(x - 2)}^{2} + 2$ D、 $y = {(x + 2)}^{2} - 2$

查看试题解析
5. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．其中第九卷，主要讲述了以测量问题为中心的直角三角形三边互求的关系．其中记载：“今有邑，东西七里，南北九里，各中开门，出东门一十五里有木，问：出南门几何步而见木？”
译文：“今有一座长方形小城，东西向城墙长7里，南北向城墙长9里，各城墙正中均开一城门．走出东门15里处有棵大树，问走出南门多少步恰好能望见这棵树？”（注：1里 $= 300$ 步）你的计算结果是：出南门（）步而见木．

A、205 B、215 C、305 D、315

查看试题解析
6. 如图，在⊙O中，弦AB，CD相交于点P，若∠A＝50°，∠APD＝82°，则∠B的大小是（　　）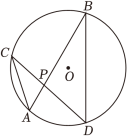

A、32° B、42° C、48° D、52°

查看试题解析
7. 已知 $∠ A + ∠ B = 90 °$ ，且 $c o s A = \frac{3}{5}$ ，则 $t a n B$ 的值为（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
8. 如图，若将上图正方形剪成四块，恰能拼成下图的矩形，设 $a = 1$ ，则 $b =$ （　　　）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{\sqrt{5} + 1}{2}$ C、 $\frac{\sqrt{5} + 3}{2}$ D、 $\sqrt{2} + 1$

查看试题解析

二、填空题（共8小题，每小题3分，满分24分）

9. 已知抛物线 $y = x^{2} + 2 x + m$ 与 $x$ 轴有且只有一个公共点，则 $m =$ ．

查看试题解析
10. 已知 $a 、 b$ 是一元二次方程 $3 x^{2} - x - 1 = 0$ 的两根，则 $\frac{1}{a} + \frac{1}{b} =$ ．

查看试题解析
11. 已知 $\frac{a}{b} = \frac{c}{d} = \frac{4}{5}$ $(b - d \neq 0)$ ，则 $\frac{a - c}{b - d}$ ＝．

查看试题解析
12. 已知函数 $y = (m - 3) x^{m^{2} - 7}$ 是二次函数，则m＝.

查看试题解析
13. 如图，若反比例函数 $y = \frac{k}{x} (x < 0)$ 的图像经过点A， $A B ⊥ x$ 轴于B，且 $△ A O B$ 的面积为3，则k的值为．

查看试题解析
14. 如图所示，在边长相同的小正方形组成的网格中，两条经过格点的线段相交所成的锐角为 $α$ ，则夹角 $α$ 的正弦值为．

查看试题解析
15. 江南水乡苏州现存100多座石拱桥，已知（如图）一石拱桥的桥顶到水面的距离 $C D$ 为 $8 m$ ，桥拱半径 $O C$ 为 $5 m$ ，则水面宽 $A B =$ $m$ ．

查看试题解析
16. 如图，在四边形 $A B C D$ 中， $A D ∥ B C$ ， $B E$ 平分 $∠ A B C$ 交 $C D$ 于 $E$ ，且 $B E ⊥ C D$ ， $C E ： E D = 2 ： 1$ ．如果 $△ B E C$ 的面积为2，那么四边形 $A B C D$ 的面积是．

查看试题解析

三、解答题（共10小题，满分72分）

17. 计算： $t a n 60 ° \cdot s i n 30 ° + \frac{\sqrt{2}}{2 s i n 45 °} - 2 | c o s 60 ° - 1 |$ ．

查看试题解析
18. 解方程： $x^{2} - 8 x + 12 = 0$

查看试题解析
19. 如图，一次函数 $y = a x + b$ 与反比例函数 $y = \frac{k}{x}$ 的图象交于点 $A (1 ， 3)$ ， $B (m ， - 1)$ ．

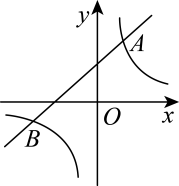(1)、求反比例函数和一次函数的表达式．

(2)、根据图象，当x取何值时，一次函数的值大于反比例函数的值？

查看试题解析
20. 某商场经销A玩具，购进时的单价是60元．按照要求，销售时单件利润率不得超过 $40 %$ ．根据市场调查，销售单价定为80元时，每天可以卖出200件，而销售单价每降低1元，每天就可多售出20件．求销售单价定为多少时，该商场每天销售A玩具可以获利2500元．

查看试题解析
21. 安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害，为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动．在活动前和活动后分别随机抽取了部分使用电瓶车的市民，就骑电瓶车戴安全帽情况进行问卷调查，将收集的数据制成如下统计图表．

(1)、宣传活动前，在抽取的市民中哪一类别的人数最多？占抽取人数的百分之几？

(2)、该市约有 $30$ 万人使用电瓶车，请估计活动前全市骑电瓶车“都不戴”安全帽的总人数；

(3)、小明认为，宣传活动后骑电瓶车“都不戴”安全帽的人数为 $178$ ，比活动前增加了1人，因此交警部门开展的宣传活动没有效果．小明分析数据的方法是否合理？请结合统计图表，对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法．

查看试题解析
22. 如图， $⊙ O$ 是 $R t △ A B C$ 的外接圆， $∠ A B C = 90 °$ ， $B E$ 平分 $∠ A B C$ 交 $⊙ O$ 于E ，过B作 $B D ⊥ E C$ 的延长线于D ．

(1)、若 $A B = B E$ ，求证： $∠ B C A = ∠ B A E$ ；

(2)、若 $A B = 12$ ， $B C = 5$ ，求 $A E$ 的长度．

查看试题解析
23. 如图，一座古塔坐落在小山上（塔顶记作点 $A$ ，其正下方水平面上的点记作点 $B$ ），小李站在附近的水平地面上，他想知道自己到古塔的水平距离，便利用无人机进行测量，但由于某些原因，无人机无法直接飞到塔顶进行测量，因此他先控制无人机从脚底（记为点C）出发向右上方（与地面成45°，点A ， B ， C ， O在同一平面）的方向匀速飞行4秒到达空中O点处，再调整飞行方向，继续匀速飞行8秒到达塔顶，已知无人机的速度为5米/秒， $∠ A O C = 7 5^{∘}$ ，求小李到古塔的水平距离即 $B C$ 的长. （结果精确到 $1 m$ ，参考数据： $\sqrt{2} \approx 1.41 ， \sqrt{3} \approx 1.73$ ）

查看试题解析
24. 2023年5月8日，国产大飞机 $C 919$ 商业首航完成，12时31分在北京首都机场，穿过隆重的“水门礼”（寓意“接风洗尘”）．如图1，两辆消防车面向飞机喷射水柱，喷射的两条水柱近似看作形状相同的抛物线的一部分．如图2，当两辆消防车喷水口A ， B的水平距离为80米时，两条水柱在抛物线的顶点H处相遇，此时相遇点H距地面20米，喷水口A ， B距地面均为4米．若两辆消防车同时后退10米（两条水柱的形状及喷水口 $A^{'}$ ， $B^{'}$ 到地面的距离均保持不变，按照图中所示建立平面直角坐标系），此时两条水柱相遇点 $H^{'}$ 距地面多少米？

查看试题解析
25. 如图，在矩形ABCD中， $A B = 3 c m$ ， $B C = 6 c m$ ，动点M以 $1 c m / s$ 的速度从A点出发，沿 $A B$ 向点B运动，同时动点N以 $2 c m / s$ 的速度从点D出发，沿DA向点A运动，设运动的时间为 $t$ 秒（ $0 < t < 3$ ）．

(1)、当 $t$ 为何值时， $△ A M N$ 的面积等于矩形 $A B C D$ 面积的 $\frac{1}{9}$ ？

(2)、是否存在某一时刻 $t$ ，使得以A、M、N为顶点的三角形与 $△ A C D$ 相似?若存在，求出 $t$ 的值；若不存在，请说明理由．

查看试题解析
26. 已知在平面直角坐标系中，抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 与x轴相交于点A，B，与y轴相交于点C，直线y=x+4经过A，C两点，

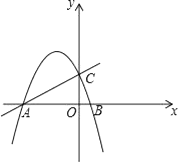(1)、求抛物线的表达式；

(2)、如果点P，Q在抛物线上（P点在对称轴左边），且PQ∥AO，PQ=2AO，求P，Q的坐标；

(3)、动点M在直线y=x+4上，且△ABC与△COM相似，求点M的坐标．

查看试题解析