湖南省衡阳市祁东县2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、选择题（在下列各题的四个选项中，只有一项是符合题意的．请在答题卡中填涂符合题意的选项．本大题共10小题，每小题3分，共30分）

1. 式子 $\sqrt{x - 3}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x ≥ 3$ B、 $x > 3$ C、 $x \leq 3$ D、 $x \neq 3$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ B、 $\sqrt{16} - \sqrt{4} = 4$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{(- 3)^{2}} = - 3$

查看试题解析
3. 下列事件是必然事件的是（）

A、买中奖率为 $\frac{1}{20}$ 的奖券20张，中奖 B、打开电视机，正在播放新闻 C、抛掷一枚质地均匀的硬币100次，正面朝上的次数为50次 D、三角形内角和是 $180 °$

查看试题解析
4. 在 $△ A B C$ 中， $∠ A B C = 90 °$ ．若 $A C = 10$ ， $s i n A = \frac{3}{5}$ ，则 $A B$ 的长是（）

A、 $\frac{6}{5}$ B、 $\frac{50}{3}$ C、6 D、8

查看试题解析
5. 若点 $A (1 ， 2)$ 向下平移2个单位长度得到对应点 $A^{'}$ ，则点 $A^{'}$ 的坐标是（）

A、 $(- 1 ， 2)$ B、 $(1 ， 0)$ C、 $(1 ， 4)$ D、 $(3 ， 2)$

查看试题解析
6. 抛物线 $y = - \frac{1}{2} x^{2} - 3$ 的顶点坐标是（）

A、 $(\frac{1}{2} ， - 3)$ B、 $(- 3 ， 0)$ C、 $(0 ， - 3)$ D、 $(0 ， 3)$

查看试题解析
7. 如图，已知点D ， E ， F分别是 $A B ， B C ， C A$ 的中点， $△ A B C$ 的周长为 $12$ ，则 $△ D E F$ 的周长是（）

A、6 B、7 C、8 D、 $10$

查看试题解析
8. 如图，为了估算河的宽度，我们可以在河对岸的岸边选定一个目标记为点A ，再在河的这一边选点B和点C ，使得 $A B ⊥ B C$ ，然后再在河岸上选点E ，使得 $E C ⊥ B C$ ，设 $B C$ 与 $A E$ 交于点D ，测得 $B D = 120$ 米， $D C = 60$ 米， $E C = 50$ 米，那么这条河的大致宽度是（）

A、 $120$ 米 B、 $100$ 米 C、 $75$ 米 D、 $25$ 米

查看试题解析
9. 在平面直角坐标系中，已知点 $A (- 4 ， 2)$ ， $B (- 6 ， - 4)$ ，以原点 $O$ 为位似中心，相似比为 $\frac{1}{2}$ ，把 $△ A B O$ 缩小，则点 $A$ 的对应点 $A^{'}$ 的坐标是（）

A、 $(- 2 ， 1)$ B、 $(- 8 ， 4)$ C、 $(- 2 ， 1)$ 或 $(2 ， - 1)$ D、 $(- 8 ， 4)$ 或 $(8 ， - 4)$

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c$ 的顶点坐标为 $(- 1 ， n)$ ，其部分图象如图所示，下列结论：① $a b c > 0$ ；② $9 a + 3 b + c < 0$ ③若点 $M (- \frac{3}{2} ， y_{1})$ ，点 $N (\frac{1}{2} ， y_{2})$ 是函数图象上的两点，则 $y_{1} < y_{2}$ ；④关于x的方程 $a x^{2} + b x + c = n + 1$ 无实数根；其中正确结论有（）

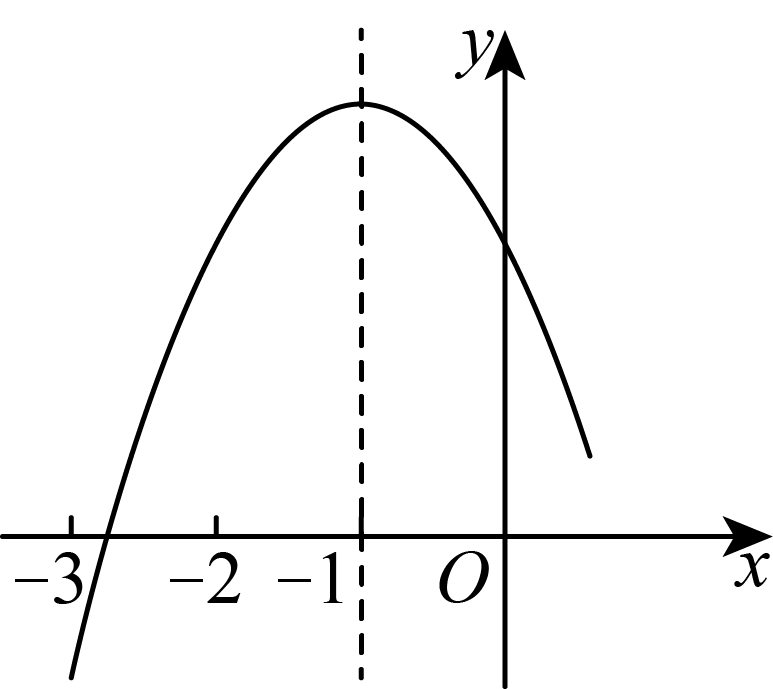A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

11. 方程 $x^{2} - 3 x = 0$ 的根为.

查看试题解析
12. 已知 $\frac{a}{b} = \frac{3}{2}$ ，则 $\frac{4 a - 3 b}{b} =$ ．

查看试题解析
13. 若关于 $x$ 的方程 $x^{2} - 2x - m=0$ 有两个相等的实数根，则 $m$ 的值是.

查看试题解析
14. 一个袋子中只装有红、白两种颜色的球，这些球的形状、质地等完全相同，其中白色球有3个，红色球有n个．在看不到球的条件下，随机地从袋子中摸出一个球，记录下颜色后，放回袋子中并摇匀．同学们进行了大量重复试验，发现摸出白球的频率稳定在 $0.2$ 附近，则n的值约为．

查看试题解析
15. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $D$ 是 $A B$ 的中点， $C D = 5$ ，则 $A B =$ ．

查看试题解析
16. 某滑雪场举办冰雪嘉年华活动，采用直升机航拍技术拍摄活动盛况．如图，通过直升机的镜头C观测水平雪道一端A处的俯角为 $30 °$ ，另一端B处的俯角为 $45 °$ ．若直升机镜头C处的高度 $C D$ 为300米，点A ， D ， B在同一直线上，则雪道 $A B$ 的长度为米．

查看试题解析

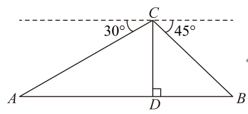
三、解答题（本大题共9小题，共72分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）

17. 计算： $\sqrt{15} \div \sqrt{5} - \sqrt{12} + (3.14 - π)^{0} + 2 s i n 60 °$ ．

查看试题解析
18. 若关于x的一元二次方程 $x^{2} - m x + 2 = 0$ 有一个根是 $x = 2$ ，求m的值及方程的另一个根．

查看试题解析
19. 如图是某区域的平面示意图，码头A在观测站B的正东方向，码头A的北偏西 $60^{°}$ 方向上有一小岛C ，小岛C在观测站B的北偏西 $15^{°}$ 方向上，码头A到小岛C的距离AC为10海里．

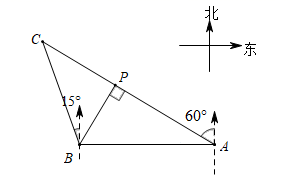(1)、填空： $∠ B A C =$ 度， $∠ C =$ 度；

(2)、求观测站B到AC的距离BP（结果保留根号）．

查看试题解析
20. 为了参加全市中学生“党史知识竞赛”，某校准备从甲、乙2名女生和丙、丁2名男生中任选2人代表学校参加比赛.

(1)、如果已经确定女生甲参加，再从其余的候选人中随机选取1人，则女生乙被选中的概率是；

(2)、求所选代表恰好为1名女生和1名男生的概率.

查看试题解析
21. 为建设宜居宜业美丽乡村，某县 $2021$ 年投入资金 $1000$ 万元， $2023$ 年投入资金 $1440$ 万元，现假定 $2021$ 年到 $2023$ 年每年投入资金的增长率相同．

(1)、求该县投入资金的年平均增长率；

(2)、按照这个增长率，预计该县 $2024$ 年投入资金为多少万元？

查看试题解析
22. 学校要围一个矩形花圃，花圃的一边利用足够长的墙，另三边用总长为36米的篱笆恰好围成（如图所示）．设矩形的一边 $A B$ 的长为x米（要求 $A B < A D$ ），矩形 $A B C D$ 的面积为S平方米．

(1)、求S与x之间的函数关系式，并直接写出自变量x的取值范围；

(2)、要想使花圃的面积最大， $A B$ 边的长应为多少米？

查看试题解析
23. 如图，四边形ABCD为平行四边形，E为边AD上一点，连接AC、BE ，它们相交于点F ，且∠ACB＝∠ABE ．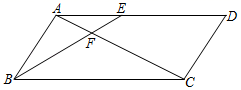

(1)、求证：AE²＝EF•BE；

(2)、若AE＝2，EF＝1，CF＝4，求AB的长．

查看试题解析
24. 已知抛物线 $y = x^{2} - 2 x - 3$ ．

(1)、求出它的顶点坐标和对称轴；

(2)、当 $- 2 \leq x \leq 2$ 时，有 $b \leq y \leq a$ ，求 $a b$ 的值；

(3)、当自变量x满足 $m ≤ x ≤ m + 1$ 时，此函数的最大值为p ，最小值为q ，且 $p - q = 2$ ，求m的值．

查看试题解析
25. 在平面直角坐标系 $x O y$ 中，已知抛物线 $y = a x^{2} - 3 a x + c$ 与x轴分别交于 $A (- 1 ， 0)$ ， B两点，与y轴交于点 $C (0 ， - 2)$ ．

(1)、求抛物线的函数表达式；

(2)、如图1，点D为第四象限抛物线上一点，连接 $A D ， B C$ 交于点E ，求 $\frac{D E}{A E}$ 的最大值；

(3)、如图2，连接 $A C ， B C$ ，过点O作直线 $l ∥ B C$ ，点P ， Q分别为直线l和抛物线上的点，试探究：在第一象限是否存在这样的点P ， Q ，使 $△ P Q B ∽ △ C A B$ ．若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析