湖南省娄底市2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、选择题(本大题共12道小题，共36分

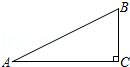
1. 下列函数是y关于x的反比例函数的是（　　）

A、y＝ $\frac{1}{x + 1}$ B、y＝ $\frac{1}{x^{2}}$ C、y＝﹣ $\frac{1}{2 x}$ D、y＝﹣ $\frac{x}{2}$

查看试题解析
2. 已知 $\frac{x}{y} = \frac{3}{5}$ ，则下列式子不成立的是（）

A、 $5 x = 3 y$ B、 $3 x = 5 y$ C、 $\frac{5}{y} = \frac{3}{x}$ D、 $\frac{y}{x} = \frac{5}{3}$

查看试题解析
3. 方程 $x^{2} = x$ 的根是（）

A、 $x = 0$ B、 $x = \pm 1$ C、 $x_{1} = 0$ ， $x_{2} = 1$ D、 $x = 1$

查看试题解析
4. 如图，△ABC中，∠C=90°，AC=2，BC=1，则cosB的值是（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
5. 关于反比例函数 $y = - \frac{6}{x}$ 的图象和性质，下列说法不正确的是（）

A、函数图象经过点 $(- 3 ， 2)$ B、函数图象在第二、四象限 C、比例系数是 $- 6$ D、当 $x > 0$ 时， $y$ 随 $x$ 的增大而减小

查看试题解析
6. 一个学习小组有 $x$ 人，春节期间，每两人互送贺卡一张，若全组共送出贺卡 $56$ 张，则（）

A、 $\frac{1}{2} x (x - 1) = 56$ B、 $\frac{1}{2} x (x + 1) = 56$ C、 $x (x - 1) = 56$ D、 $x (x + 1) = 56$

查看试题解析
7. 在三角形 $A B O$ 中，已知点 $A (- 6 ， 3)$ ， $B (- 6 ， - 4)$ ，以原点O为位似中心，相似比为 $\frac{1}{3}$ ，把 $△ A B O$ 缩小，则点A的对称点 $A ′$ 的坐标是（）

A、 $(- 2 ， 1)$ B、 $(- 8 ， 4)$ C、 $(- 8 ， 4)$ 或 $(8 ， - 4)$ D、 $(- 2 ， 1)$ 或 $(2 ， - 1)$

查看试题解析
8. 如图所示（图像在第二象限），若点 $A$ 在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像上， $A M ⊥ x$ 轴于点 $M$ ， $△ A M O$ 的面积为 $3$ ，则 $k$ 的值为（）

A、 $6$ B、 $3$ C、 $- 3$ D、 $- 6$

查看试题解析
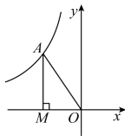9. 《九章算术》中记载了一种测量古井水面以上部分深度的方法．如图所示，在井口A处立一根垂直于井口的木杆AB ，从木杆的顶端B观察井水水岸D ，视线BD与井口的直径AC交于点E ，如果测得 $A B = 1$ 米， $A C = 1.6$ 米， $A E = 0.4$ 米，那么CD为（）米．

A、5 B、4 C、3 D、2

查看试题解析
10. 西周时期，丞相周公旦设置过一种通过测定日影长度来确定时间的仪器，称为圭表，如图是一个根据北京的地理位置设计的圭表，其中，立柱 $A C$ 高为 $a$ ，已知，冬至时北京的正午日光入射角 $∠ A B C$ 约为 $26.5 °$ ，则立柱根部与圭表的冬至线的距离（即 $B C$ 的长）约为（）

A、 $a s i n 26.5 °$ B、 $\frac{a}{c o s 26 . 5^{∘}}$ C、 $a c o s 265 °$ D、 $\frac{a}{t a n 26 . 5^{∘}}$

查看试题解析
11. 如图，直线y=x+2与反比例函 $y = \frac{k}{x}$ 的图像在第一象限交于点P ．若 $O P = \sqrt{20}$ ，则k的值为（）

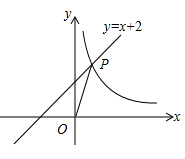A、6 B、8 C、10 D、12

查看试题解析
12. 如图，已知顶点为（﹣3，﹣6）的抛物线y=ax²+bx+c经过点（﹣1，﹣4），则下列结论中错误的是（　　）

A、b²＞4ac B、ax²+bx+c≥﹣6 C、若点（﹣2，m），（﹣5，n）在抛物线上，则m＞n D、关于x的一元二次方程ax²+bx+c=﹣4的两根为﹣5和﹣1

查看试题解析

二、填空题(本大题共6道小题，共18分

13. 从1000个零件中任意抽取100个检测，有2个不合格，估计这1000个零件中合格的零件约有个．

查看试题解析
14. 若 $y = (m + 1) x^{m^{2} - m} + 3 x$ 是y关于x的二次函数，则 $m =$ ．

查看试题解析
15. 大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点 $(A P > P B)$ ，如果 $A B$ 的长度为 $8 c m$ ，那么 $A P$ 的长度为 $c m$ ．

查看试题解析
16. 如图，有一个矩形苗圃园，其中一边靠墙（墙长为 $15 m$ ），另外三边用长为 $16 m$ 的篱笆围成，则这个苗圃园面积的最大值为．

查看试题解析
17. 定义：在平面直角坐标系中，点 $M (x_{0} ， y_{0})$ 到直线 $l ： y = k x + b$ 的距离 $d = \frac{| k x_{0} + b - y_{0} |}{\sqrt{k^{2} + 1}}$ ，问：点 $(- 2 ， 3)$ )到 $y = \frac{3}{4} x - \frac{1}{2}$ 的距离为．

查看试题解析
18. 如图，在由10个完全相同的正三角形构成的网格图中，∠α、∠β如图所示，则sin（α+β）＝．

查看试题解析

三、解答题（共66分，第19、20题各6分；第21、22题各8分；第23、24题各9分；第25、26题各10分）

19. 计算： $4 \sqrt{3} c o s 30 ° - \sqrt{2} s i n 45 ° + 2 c o s 60 ° t a n 45 °$ ．

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} - 2 x - m = 0$ 有实数根．

(1)、求m的取值范围；

(2)、若两实数根分别为 $x_{1}$ 和 $x_{2}$ ，且 ${x_{1}}^{2} + {x_{2}}^{2} = 6$ ，求m的值．

查看试题解析
21. 如图，在矩形 $A B C D$ 中， $A B = 6$ ， $B C = 4$ ， $E$ 是边 $B C$ 上的一点（不与 $B$ 、 $C$ 重合）， $D F ⊥ A E$ ，垂足为 $F$ ．

(1)、求证： $△ A B E ∽ △ D F A$ ；

(2)、若 $S_{△ D F A} = \frac{1}{3} S_{△ A B E}$ ，求 $B E$ 的长．

查看试题解析
22. 人口自然增长率（人口自然增长率 $=$ 人口出生率 $-$ 人口死亡率）是反映人口自然增长的趋势和速度的指标．根据对多年的人口出生率和死亡率的数据进行了整理、描述和分析，形成了如下统计表和统计图．
指标
2015年
2016年
2017年
2018年
2019年
2020年
2021年
2022年
人口出生率(‰)
11.99
13.57
12.64
10.86
10.4
8.52
7.52
6.77
人口死亡率(‰)
7.07
7.04
7.06
7.08
7.09
7.07
7.18
7.37

(1)、求2022年的人口自然增长率．

(2)、从2015年—2022年，年的人口自然增长率最大．

(3)、下列推断合理的是．（只填序号）
①2015年—2016年，人口出生率呈上升趋势；2016年—2022年，人口出生率呈下降趋势；
②人口自然增长率从2016年起持续呈下降趋势，是因为人口死亡率持续呈上升趋势；
③优化三孩生育政策有利于应对我国人口减少问题．

查看试题解析
23. 为积极响应新旧动能转换．提高公司经济效益．某科技公司近期研发出一种新型高科技设备，每台设备成本价为30万元，经过市场调研发现，每台售价为40万元时，年销售量为600台；每台售价为45万元时，年销售量为550台．假定该设备的年销售量y(单位∶台)和销售单价 $x$ (单位∶万元)成一次函数关系．

(1)、求年销售量 $y$ 与销售单价 $x$ 的函数关系式；

(2)、根据相关规定，此设备的销售单价不得高于70万元，如果该公司想获得10000万元的年利润．则该设备的销售单价应是多少万元？

查看试题解析
24. 构建几何图形解决代数问题是“数形结合”思想的体现，在计算 $t a n 15 °$ 时，如图1，在 $R t △ A C B$ 中， $∠ C = 90 ° ， ∠ A B C = 30 °$ ，延长 $C B$ 使 $B D = A B$ ，连接 $A D$ ，得 $∠ D = 15 °$ ，所以 $t a n 15 ° = \frac{A C}{C D} = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ．类比这种方法，

(1)、类比这种方法，求得 $t a n 22.5 ° =$ ；

(2)、如图2，锐角 $∠ A B C = α$ ，已知 $t a n α = m$ ，求证： $t a n \frac{α}{2} = \frac{\sqrt{m^{2} + 1} - 1}{m}$ ．

查看试题解析
25. 如图，一次函数 $y = x + 1$ 与反比例函数 $y = \frac{k}{x}$ 的图像相交于点 $A (2 ， 3)$ 和点 $B$ ．

(1)、求反比例函数的解析式；

(2)、过点 $B$ 作 $B C ⊥ x$ 轴于 $C$ ，求 $S_{△ A B C}$ ；

(3)、过点 $B$ 作 $B C ⊥ x$ 轴于 $C$ ，问：是否在 $y$ 轴上存在一点 $D$ ，使得 $B D + C D$ 的值最小，若存在，求出 $D$ 的坐标；若不存在，说明理由．

查看试题解析
26. 如图，在平面直角坐标系中，点 $A (1 ， 2)$ ， $B (5 ， 0)$ ，抛物线 $y = a x^{2} - 2 a x (a > 0)$ 交x轴正半轴于点C ，连结 $A O$ ， $A B$ ．

(1)、求点C的坐标和直线 $A B$ 的表达式；

(2)、设抛物线 $y = a x^{2} - 2 a x (a > 0)$ 分别交边 $B A$ ， $B A$ 延长线于点D ， E ．
①若 $△ C D B$ 与 $△ B O A$ 相似，求抛物线表达式；
②若 $△ O A E$ 是等腰三角形，则a的值为 ▲ （请直接写出答案即可）．

查看试题解析

指标	2015年	2016年	2017年	2018年	2019年	2020年	2021年	2022年
人口出生率(‰)	11.99	13.57	12.64	10.86	10.4	8.52	7.52	6.77
人口死亡率(‰)	7.07	7.04	7.06	7.08	7.09	7.07	7.18	7.37