湖南省岳阳市2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、选择题（本题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1. $\frac{1}{2023}$ 的绝对值是（）

A、 $\frac{1}{2023}$ B、 $- \frac{1}{2023}$ C、－2023 D、2023

查看试题解析
2. 计算 $- a^{3} + 2 a^{3}$ 的结果为（）

A、 $a^{3}$ B、 $- a^{3}$ C、 $3 a^{3}$ D、 $- 3 a^{3}$

查看试题解析
3. 下列方程中为一元一次方程的是（）

A、 $2 x + 3 = 0$ B、 $2 x + y = 3$ C、 $x^{2} + x = 3$ D、 $x - \frac{2}{x} = 3$

查看试题解析
4. 以下调查中，最适宜采用普查方式的是（）

A、检测某批次汽车的抗撞击能力 B、调查全国中学生视力和用眼卫生情况 C、调查黄河的水质情况 D、检查我国“神舟十三号”飞船各零部件的情况

查看试题解析
5. 某一学习小组共有8人，在一次数学测验中，得100分的1人，得90分的2人，得74分的4人，得64分的1人，那么这个小组的平均成绩是（）

A、82分 B、80分 C、74分 D、90分

查看试题解析
6. 下列判断正确的是（）

A、单项式a的次数是0 B、单项式﹣2a²bc的系数是2 C、单项式﹣ $\frac{1}{3}$ xy²z的次数是2 D、多项式3xy³+5x²﹣8是四次三项式

查看试题解析
7. 如图，一副三角尺按不同的位置摆放，摆放位置中∠α与∠β一定相等的图形个数共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 已知多项式A＝2x³﹣2mx²+3x﹣1，B＝﹣x³+2x²+nx+6，若A﹣B的结果中不含x²和x项，则m ， n的值为（　　）

A、m＝﹣1，n＝3 B、m＝﹣1，n＝﹣3 C、m＝1，n＝3 D、m＝1，n＝﹣3

查看试题解析
9. 我国元朝朱世杰所著的《算学启蒙》（1299年）记载：良马日行二百四十里，驽马日行一百五十里，驽马现行一十二日，问良马几何追及之．翻译为：跑得快的马每天走240里，跑得慢的马每天走150里，慢马先走12天，快马追上慢马的时间为（　　）

A、12天 B、15天 C、20天 D、24天

查看试题解析
10. 如图，将一张长方形纸片ABCD沿对角线BD折叠后，点C落在点E处，连接BE交AD于F，再将三角形DEF沿DF折叠后，点E落在点G处，若DG刚好平分∠ADB，则∠EDF的度数是（）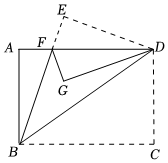

A、18° B、30° C、36° D、20°

查看试题解析

二、填空题（本题共6小题，每小题3分，满分18分）

11. 比较大小： $- 2$ 1（填“ $>$ ， $<$ 或 $=$ ”符号）

查看试题解析
12. 如果一个角与它的余角之比为1：2，那么这个角的补角度数是．

查看试题解析
13. 若 $x = - 2$ 是关于 $x$ 的方程 $3 x + 7 = \frac{x}{2} - a$ 的解，则 $a$ 的值等于.

查看试题解析
14. 袁隆平院士被誉为“杂交水稻之父”，经过他带领的团队多年艰苦努力，目前我国杂交水稻种植面积达2.4亿亩，每年增产的粮食可以养活80000000人．将80000000这个数用科学记数法可表示为．

查看试题解析
15. 小忆对全班同学最喜爱丹顶鹤的人数运用划记法记录数据进行统计，喜欢的人数记，“正正”，经统计喜欢丹顶鹤的人数有人，占全班人数的 $25 %$ ，则全班共有人．

查看试题解析
16. 已知 $a$ ， $b$ ， $c$ ， $d$ 为有理数，现规定一种新的运算 $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ ，那么当 $| \begin{array}{l} 3 & 4 \\ (2 - x) & 5 x \end{array} | = 18$ 时， $x$ 的值是．

查看试题解析

三、解答题（本题共9小题，满分72分，解答应写出文字说明，证明过程或演算步骤）

17. 计算：

(1)、 $- 9 + 5 \times (- 6) - (- 4)^{2} \div (- 8)$ ；

(2)、 $(- \frac{1}{12} + \frac{3}{4} - \frac{1}{6}) \times (- 24)$ ．

查看试题解析
18. 先化简，再求值： $6 a b^{2} - (a b^{2} + 3 a^{2} b) + 5 (3 a^{2} b - a b^{2})$ ，其中 $a = \frac{1}{2}$ ， $b = - 1$ ．

查看试题解析
19. 已知线段 $A B = 12 c m$ ，在直线 $A B$ 上有一点 $C$ ，且 $B C = 6 c m$ ， D是线段 $A C$ 的中点，求线段 $B D$ 的长.（请先画出符合题意的图形，再解答该问题）

查看试题解析
20. 解方程：

(1)、 $7 x + 5 = 2 - 8 x$ ；

(2)、 $\frac{2 x - 1}{3} = 1 - \frac{x + 2}{2}$ ．

查看试题解析
21. 如图所示，点A，O，B在同一条直线上， $O D$ 平分 $∠ A O C$ ， $O E$ 平分 $∠ B O C$ ．

(1)、若 $∠ B O D = 160 °$ ，求 $∠ B O E$ 的度数．

(2)、若 $∠ C O E$ 比 $∠ C O D$ 多 $60 °$ ，求 $∠ C O E$ 的度数．

查看试题解析
22. 小明在解方程 $\frac{2 x - 1}{3} = \frac{x + m}{4} - 1$ ，方程两边都乘以各分母的最小公倍数去分母时，漏乘了不含分母的项﹣1，得到方程的解是x＝3，请你帮助小明求出m的值和原方程正确的解.

查看试题解析
23. 祁阳县某中学校团委开展“关爱残疾学生”爱心捐书活动，全校师生踊跃捐赠各类书籍共3000本．为了解各类书籍的分布情况，从中随机抽取了部分书籍分四类进行统计：A．艺术类；B．文学类；C．科普类；D．其他，并将统计结果绘制成如图所示的两幅不完整的统计图．

(1)、这次统计共抽取了书籍，扇形统计图中的m= ， ∠α的度数是

(2)、请将条形统计图补充完整；

(3)、估计全校师生共捐赠了多少本文学类书籍．

查看试题解析
24. 为了打赢蓝天保卫战，某市环保局对一段长 $2400 m$ 的河道进行整治，整治任务由甲、乙两个工程队来完成．已知甲工程队每天完成 $30 m$ ，乙工程队每天完成 $50 m$ ．

(1)、若该任务由甲、乙两个工程队合作完成，则整治这段河道需要多少天？

(2)、若甲工程队先单独整治一段时间后离开，剩下的由乙工程队来完成，两队共用时 $60$ 天，求甲、乙工程队分别整治了多长的河道．

查看试题解析
25. 已知数轴上的两点A、B所表示的数分别是a和b，O为数轴上的原点，如果有理数a，b满足 $| a + 8 | + {(b - 22)}^{2} = 0.$

(1)、求a和b的值；

(2)、若点P是一个动点，以每秒5个单位长度的速度从点A出发，沿数轴向右运动，请问经过多长时间，点P恰巧到达线段AB的三等分点？

(3)、若点C是线段AB的中点，点M以每秒3个单位长度的速度从点C开始向右运动，同时点P以每秒5个单位长度的速度从点A出发向右运动，点N以每秒4个单位长度的速度从点B开始向左运动，点P与点M之间的距离表示为PM，点P与点N之间的距离表示为PN，是否存在某一时刻使得PM+PN=12？若存在，请求出此时点P表示的数；若不存在，请说明理由.

查看试题解析