湖南省衡阳市2023-2024学年七年级上学期期末联考数学试题
试卷更新日期:2024-03-13 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 的相反数是( )A、 B、2024 C、 D、2. 在 , , , 四个数中,最大的一个数是( )A、 B、 C、 D、3. 下列几何体中,从正面、左面、上面三个方向看到的几何体的形状图完全相同的是( )A、
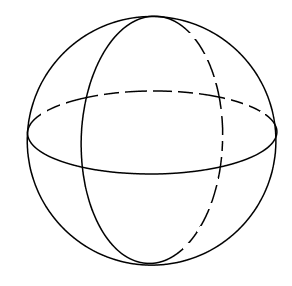 B、
B、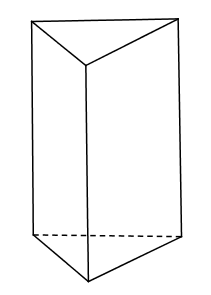 C、
C、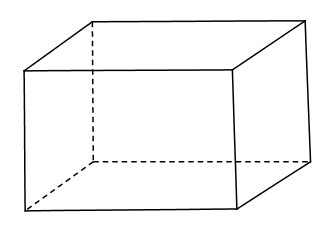 D、
D、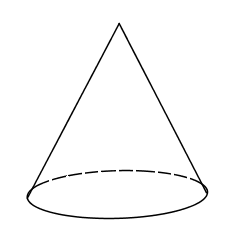 4. 在下列说法中,正确的是( )A、是单项式 B、的次数为4 C、的系数为 D、不是整式5. 下列运算正确的是( )A、 B、 C、 D、6. 与的和的平方,用式子表示,正确的是( )A、 B、 C、 D、7. 如图,已知 , , 若 , 则的度数是( )
4. 在下列说法中,正确的是( )A、是单项式 B、的次数为4 C、的系数为 D、不是整式5. 下列运算正确的是( )A、 B、 C、 D、6. 与的和的平方,用式子表示,正确的是( )A、 B、 C、 D、7. 如图,已知 , , 若 , 则的度数是( ) A、 B、 C、 D、8. 下面四种现象:①小狗看到远处的食物,总是径直奔向食物;②打开手电筒后射出的光线;③扔一个小石子,石子在空中飞行的路线;④将弯曲的河道改直,可以缩短航程.其中可以用“两点之间,线段最短”来解释的现象有( )A、①② B、②③ C、①④ D、①③④9. 如图所示是一个计算机程序图,如果开始输入 , 那么最后输出的结果为( )
A、 B、 C、 D、8. 下面四种现象:①小狗看到远处的食物,总是径直奔向食物;②打开手电筒后射出的光线;③扔一个小石子,石子在空中飞行的路线;④将弯曲的河道改直,可以缩短航程.其中可以用“两点之间,线段最短”来解释的现象有( )A、①② B、②③ C、①④ D、①③④9. 如图所示是一个计算机程序图,如果开始输入 , 那么最后输出的结果为( ) A、 B、1 C、 D、10. 如图,直线 , 点在上,点、点在上,的角平分线交于点 , 过点作于点 , 已知 , 则的度数为( )
A、 B、1 C、 D、10. 如图,直线 , 点在上,点、点在上,的角平分线交于点 , 过点作于点 , 已知 , 则的度数为( ) A、26° B、32° C、36° D、42°
A、26° B、32° C、36° D、42°二、填空题(每题3分,共18分)
-
11. 的绝对值是.12. 月球的半径约为173800米,把 173800这个数用科学记数法表示为 .13.若3xm+5y2与x3yn的和是单项式,则mn= .14. 如图,点 在线段 上, , ,点 , 分别是 、 的中点,则线段 的长为cm
 15. 如图, , , 则当时, .
15. 如图, , , 则当时, .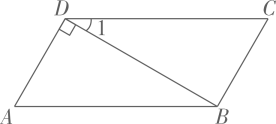 16. 如图,已知A , B两点在数轴上,点A表示的数为 , , 点M以每秒1个单位长度的速度从点A向右运动.点N以每秒3个单位长度的速度从点B向左运动(点M、N点同时出发),经过秒,点M、点N分别到原点O的距离相等.
16. 如图,已知A , B两点在数轴上,点A表示的数为 , , 点M以每秒1个单位长度的速度从点A向右运动.点N以每秒3个单位长度的速度从点B向左运动(点M、N点同时出发),经过秒,点M、点N分别到原点O的距离相等.
三、解答题(6+6+6+8+8+9+9+10+10,共72分)
-
17. 把下列各数分别填在相应的集合内:
, , , , ,
整数集合:{ ▲ …};
负数集合:{ ▲ …}
正分数集合:{ ▲ …}.
18. 计算:(1)、(2)、19. 计算:(1)、(2)、20. 在如图所示的方格中,点A、B、C均为网格点,按要求画图并回答问题: (1)、画直线AC.(2)、过点C画线段AB的垂线,垂足为点D.(3)、点C与直线AB上各点连结的所有线段中,线段CD最短的数学道理是____.A、两点之间,线段最短 B、两点确定一条直线 C、垂线段最短21. 如图,已知 , 射线交于点 , 交于点 , 从点引一条射线 , 若 , 求证: . 对于上述问题,请在以下解答过程的空白处填上适当的内容(理由或数学式).
(1)、画直线AC.(2)、过点C画线段AB的垂线,垂足为点D.(3)、点C与直线AB上各点连结的所有线段中,线段CD最短的数学道理是____.A、两点之间,线段最短 B、两点确定一条直线 C、垂线段最短21. 如图,已知 , 射线交于点 , 交于点 , 从点引一条射线 , 若 , 求证: . 对于上述问题,请在以下解答过程的空白处填上适当的内容(理由或数学式).
证明:(已知),且(对顶角相等),
( ▲ )(等量代换).
( ▲ ).
( ▲ ).
又(已知),
( ▲ )(两直线平行内错角相等).
.
22. 某灯具厂计划每天生产盏景观灯,但由于各种原因,实际每天生产景观灯盏数与计划每天生产景观灯盏数相比有出入.下表是某周的生产情况(增产记为正,减产记为负):星期
一
二
三
四
五
六
日
生产情况
-3
-5
-2
+9
-7
+12
-3
(1)、求该厂这周实际生产景观灯的盏数;(2)、该厂实行每日计件工资制,每生产一盏景观灯可得元,若超额完成任务,则超过部分每盏另奖元;若未能完成任务,则少生产一盏扣元,该厂工人这一周的工资总额是多少元?23. 已知 , .(1)、求;(2)、若 , 求的值.24. 如图,已知 , . 点P是射线AM上一动点(与点A不重合)、BC , BD分别平分和 , 分别交射线AM于点C , D . (1)、求的度数.(2)、当点P运动到使时,的度数是多少?为什么?(3)、当点P运动时,与之间的数量关系是否随之发生变化?若不变化.请写出它们之间的关系,并说明理由;若变化,请写出变化规律.25. 阅读理解:为数轴上三点,若点满足或 , 我们称点是线段的“倍点”,例如,如图1,点表示数 , 点表示数 , 点表示数 , 此时,点是线段的一个“倍点”.
(1)、求的度数.(2)、当点P运动到使时,的度数是多少?为什么?(3)、当点P运动时,与之间的数量关系是否随之发生变化?若不变化.请写出它们之间的关系,并说明理由;若变化,请写出变化规律.25. 阅读理解:为数轴上三点,若点满足或 , 我们称点是线段的“倍点”,例如,如图1,点表示数 , 点表示数 , 点表示数 , 此时,点是线段的一个“倍点”. (1)、在图2中,点表示的数为 , 点表示的数为;(2)、若点是线段的“倍点”,则点表示的数为;(3)、现有一动点从点出发,以每秒个单位的速度沿数轴向左运动,运动时间为秒,当点是线段的“倍点”时,求的值.
(1)、在图2中,点表示的数为 , 点表示的数为;(2)、若点是线段的“倍点”,则点表示的数为;(3)、现有一动点从点出发,以每秒个单位的速度沿数轴向左运动,运动时间为秒,当点是线段的“倍点”时,求的值.