湖南省岳阳市2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-03-13 类型:期末考试
一、选择题.(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 64的立方根是( )A、4 B、±4 C、8 D、±82. 下列分式中,是最简分式的是( )A、 B、 C、 D、3. 若 , 则( )A、 B、 C、 D、4. 不改变分式的值,将分式中的分子、分母的系数化为整数,其结果为( )A、 B、 C、 D、5. 下列各组二次根式中,化简后是同类二次根式的是( )A、与 B、与 C、与 D、与6. 下列各式计算正确的是 ( )A、 B、 C、 D、7. 下列说法错误的是( )A、有一个角是的等腰三角形是等边三角形 B、如果一个三角形有两个角相等,那么这两个角所对的边相等 C、等腰三角形的角平分线,中线,高相互重合 D、三个角都相等的三角形是等边三角形8. 如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )
 A、PA+PC=BC B、PA=PB C、DE⊥AB D、PA=PC9. 对于a、b定义 , 已知分式方程的解满足不等式 , 则a的取值范围是( )A、 B、 C、 D、10. 如图,已知中, , 直角的顶点P是的中点,两边分别交于点E , F , 给出以下四个结论:①;②是等腰直角三角形;③;④的最小值为1.上述结论正确的有( )个
A、PA+PC=BC B、PA=PB C、DE⊥AB D、PA=PC9. 对于a、b定义 , 已知分式方程的解满足不等式 , 则a的取值范围是( )A、 B、 C、 D、10. 如图,已知中, , 直角的顶点P是的中点,两边分别交于点E , F , 给出以下四个结论:①;②是等腰直角三角形;③;④的最小值为1.上述结论正确的有( )个 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题.(本题共6小题,每小题3分,满分18分)
-
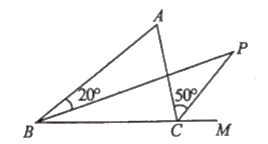
11. 分式的值为 , 则 .12. 若式子在实数范围内有意义,则x的取值范围是 .13. 如图, 是 中 的平分线, 是 的外角的平分线,如果 ,则 .
 14. 若关于x的不等式组 只有3个整数解,则m的取值范围是 .15. 关于的分式方程的解为非负数,则的取值范围 .16. 大家知道的小数部分我们不可能全部地写出来,于是可以用来表示的小数部分(因为的整数部分是1,将这个数减去其整数部分,差就是小数部分).
14. 若关于x的不等式组 只有3个整数解,则m的取值范围是 .15. 关于的分式方程的解为非负数,则的取值范围 .16. 大家知道的小数部分我们不可能全部地写出来,于是可以用来表示的小数部分(因为的整数部分是1,将这个数减去其整数部分,差就是小数部分).⑴如果的小数部分为 , 的整数部分为 , 求的值 .
⑵已知: , 其中x是整数,且 , 求的相反数 .
三、解答题.(本题共9小题,满分72分,解答应写出文字说明,证明过程或演算步骤)
-
17. 计算:(1)、;(2)、 .18. 若 .(1)、求 .(2)、求 .19. 解不等式组: ,并把解集在数轴上表示出来.20. 小华想复习分式方程,由于印刷问题,有一个数“?”看不清楚:.(1)、她把这个数“?”猜成5,请你帮小华解这个分式方程;(2)、小华的妈妈说:“我看到标准答案是:方程的增根是 , 原分式方程无解”,请你求出原分式方程中“?”代表的数是多少?21. 如图,∠A=∠B,AE=BE,∠1=∠2,点D在AC边上.
 (1)、求证:△AEC≌△BED.(2)、若∠1=40°,求∠BDE的度数.22. 如图,AD与BC相交于点O,点E、F分别为OB、OD的中点,连接AB、CD、EF,给出以下四个等量关系:① ,② ,③ ,④ .请你以其中两个为条件,另两个中的一个为结论,组成一个真命题,并证明.
(1)、求证:△AEC≌△BED.(2)、若∠1=40°,求∠BDE的度数.22. 如图,AD与BC相交于点O,点E、F分别为OB、OD的中点,连接AB、CD、EF,给出以下四个等量关系:① ,② ,③ ,④ .请你以其中两个为条件,另两个中的一个为结论,组成一个真命题,并证明. (1)、条件: , 结论:;(填序号)(2)、写出你的证明过程.23. 某校决定组织学生开展校外拓展活动,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲乙两种大客车,它们的载客量和租金如下表所示.学校计划此次拓展活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
(1)、条件: , 结论:;(填序号)(2)、写出你的证明过程.23. 某校决定组织学生开展校外拓展活动,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲乙两种大客车,它们的载客量和租金如下表所示.学校计划此次拓展活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.客车
甲种
乙种
载客量/(人/辆)
30
42
租金(元/辆)
300
400
(1)、参加此次拓展活动的老师有多少人?参加此次拓展活动的学生有多少人?(2)、既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为多少辆.(3)、你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.24. 阅读下面解题过程.例:化简 .
解: .
请回答下列问题.
(1)、归纳:请直接写出下列各式的结果:①;② .(2)、应用:化简 .(3)、拓展: . 含的式子表示,为正整数)25. (1)、观察推理:如图1,△ABC中,∠ ACB=90°,AC=BC , 直线l过点C , 点A、B在直线l同侧, BD⊥ l , AE⊥ l , 垂足分别为D、E .求证:△AEC≌△CDB;(2)、类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至A , 连接C , 求△AC的面积.(3)、拓展提升:如图3,等边△EBC中,EC=BC=6cm,点O在BC上,且OC=4 cm,动点P从点E沿射线EC以1 cm/s速度运动,连结OP , 将线段OP绕点O逆时针旋转120°得到线段OF . 要使点F恰好落在射线EB上,求点P运动的时间ts .
(1)、观察推理:如图1,△ABC中,∠ ACB=90°,AC=BC , 直线l过点C , 点A、B在直线l同侧, BD⊥ l , AE⊥ l , 垂足分别为D、E .求证:△AEC≌△CDB;(2)、类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至A , 连接C , 求△AC的面积.(3)、拓展提升:如图3,等边△EBC中,EC=BC=6cm,点O在BC上,且OC=4 cm,动点P从点E沿射线EC以1 cm/s速度运动,连结OP , 将线段OP绕点O逆时针旋转120°得到线段OF . 要使点F恰好落在射线EB上,求点P运动的时间ts .