四川省泸州市合江县教育发展研究中心2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-03-13 类型:期末考试
一、选择题(本大题共12个小题,每小题3分,共36分)
-
1. 下图是几种国产汽车奇瑞、比亚迪、长安、东风的车标,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下列每组三条线段为边,能组成三角形的是( )A、3,4,5 B、5,6,11 C、4,4,9 D、1,2,33. 某种细胞的直径是0.00000095米,将0.00000095用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 将正六边形与正五边形按如图所示的方式摆放,公共顶点为D , 且正六边形的边与正五边形的边在同一条直线上,则的度数是( )
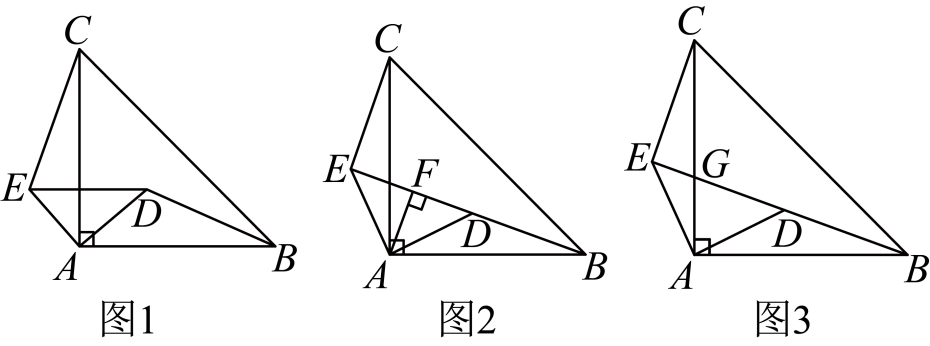
2. 以下列每组三条线段为边,能组成三角形的是( )A、3,4,5 B、5,6,11 C、4,4,9 D、1,2,33. 某种细胞的直径是0.00000095米,将0.00000095用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 将正六边形与正五边形按如图所示的方式摆放,公共顶点为D , 且正六边形的边与正五边形的边在同一条直线上,则的度数是( )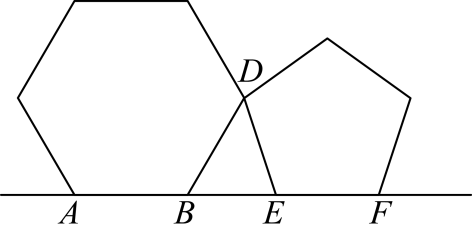 A、 B、 C、 D、6. 如图,若 , 四个点B、E、C、F在同一直线上, , , 则的长是( )
A、 B、 C、 D、6. 如图,若 , 四个点B、E、C、F在同一直线上, , , 则的长是( )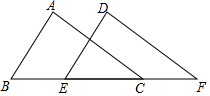 A、2 B、3 C、5 D、77. 若将分式中的x与y都扩大为原来的3倍,则这个代数式的值( )A、扩大为原来的3倍 B、不变 C、缩小为原来的 D、缩小为原来的8. 如图,在中, , , 垂直平分 , P点为直线上一动点,则周长的最小值是( )
A、2 B、3 C、5 D、77. 若将分式中的x与y都扩大为原来的3倍,则这个代数式的值( )A、扩大为原来的3倍 B、不变 C、缩小为原来的 D、缩小为原来的8. 如图,在中, , , 垂直平分 , P点为直线上一动点,则周长的最小值是( )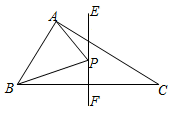 A、9 B、8 C、7 D、69. 如图,在中,的平分线与边交于点 , 与外角的平分线交于点 , 若 , 下列结论不正确的是( )
A、9 B、8 C、7 D、69. 如图,在中,的平分线与边交于点 , 与外角的平分线交于点 , 若 , 下列结论不正确的是( )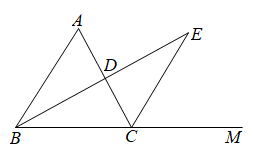 A、 B、 C、 D、10. 如图, , , 于点 , 则的长为( )
A、 B、 C、 D、10. 如图, , , 于点 , 则的长为( )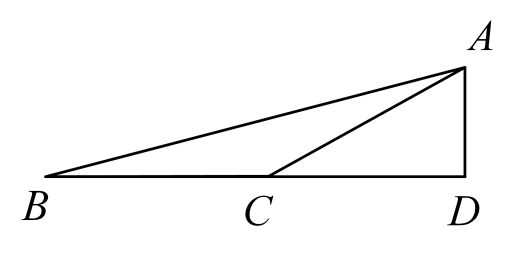 A、 B、 C、 D、11. 已知 , 则 等于( )A、3 B、5 C、 D、612. 若实数为非负数,且关于的分式方程有正数解,则符合条件的整数的和是( )A、 B、 C、 D、0
A、 B、 C、 D、11. 已知 , 则 等于( )A、3 B、5 C、 D、612. 若实数为非负数,且关于的分式方程有正数解,则符合条件的整数的和是( )A、 B、 C、 D、0二、填空题(本大题共4个小题,每小题3分,共12分)
-
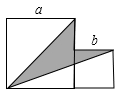
13. 如果点A(﹣1,3)和点B(a,b)关于x轴对称,那么a+b=.14. 分解因式 .15. 如图,两个正方形边长分别为a、b,且满足 , , 图中阴影部分的面积为.
 16. 如图,在Rt△ABC中,AB = CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE,EF,下列结论:①AB:BD=2:1;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤上述结论中正确的是(只填序号).
16. 如图,在Rt△ABC中,AB = CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE,EF,下列结论:①AB:BD=2:1;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤上述结论中正确的是(只填序号).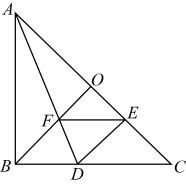
三、解答题(本大题共3个小题,每小题6分,共18分)
-
17. 计算:18. 先化简,再求值: , 其中 .19. 如图,相交于点O , , , 连接 , 求证: .

四、解答题(本大题共2个小题,每小题7分,共14分
-
20. 先化简,再求值: , 其中 .21. 如图,已知△ABC.
 (1)、作△ABC中BC边的垂直平分线EF,交AC于点E.交BC于点F(尺规作图,保留作图痕迹)(2)、连结BE.∠A=100°,∠ABC=53°求∠ABE的度数,
(1)、作△ABC中BC边的垂直平分线EF,交AC于点E.交BC于点F(尺规作图,保留作图痕迹)(2)、连结BE.∠A=100°,∠ABC=53°求∠ABE的度数,五、解答题(本大题共2个小题,每小题8分,共16分
-
22. 某大型超市购进一款热销的消毒洗衣液,由于原材料价格上涨,今年每瓶洗衣液的进价比去年每瓶洗衣液的进价上涨4元,今年用1440元购进这款洗衣液的数量与去年用1200元购进这款洗衣液的数量相同.求今年这款消毒洗衣液每瓶进价是多少元;23. 如图,在中,的平分线交于点 , 过点作;交于点 .
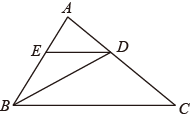 (1)、求证:;(2)、若 , 求的度数.
(1)、求证:;(2)、若 , 求的度数.六、解答题(本大题共2个小题,每小题12分,共24分