湖南省株洲市炎陵县2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-03-13 类型:期末考试
一、选择题.
-
1. 反比例函数经过点 , 则反比例函数的解析式为( )A、 B、 C、 D、2. 下列四组长度的线段中,是成比例线段的是( )A、4cm,5cm,6cm,7cm B、3cm,4cm,5cm,8cm C、5cm,15cm,3cm,9cm D、8cm,4cm,1cm,3cm3. 用配方法解方程 , 配方正确的是( )A、 B、 C、 D、4. 如果中, , 则下列结论正确的是( )A、是等边三角形 B、是钝角三角形 C、是等腰直角三角形 D、是锐角三角形5. 益阳市高新区某厂今年新招聘一批员工,他们中不同文化程度的人数见下表:
文化程度
高中
大专
本科
硕士
博士
人数
9
17
20
9
5
关于这组文化程度的人数数据,以下说法正确的是:( )
A、众数是20 B、中位数是17 C、平均数是12 D、方差是266. 把抛物线y=x2向左平移2个单位得到的抛物线是( )A、y=(x+2)2 B、y=(x﹣2)2 C、y=x2+2 D、y=x2﹣27. 某班学生毕业时,每个同学都要给其他同学写一份留言纪念,全班同学共写了1560份留言,如果全班同学有x名学生,根据题意可列方程为( )A、 B、 C、=1560 D、=15608. 如图所示,过反比例函数在第一象限内的图象上任意两点 , , 分别作轴的垂线,垂足分别为 , , 连接 , , 设与的面积为 , , 那么它们的大小关系是( ) A、 B、 C、 D、不能确定9. 如图,点A , B , C在上,若 , 则等于( )
A、 B、 C、 D、不能确定9. 如图,点A , B , C在上,若 , 则等于( ) A、 B、 C、 D、10. 二次函数的图象如图所示,图像与轴的一个交点是 , 对称轴是直线 , 下列结论正确的为( )
A、 B、 C、 D、10. 二次函数的图象如图所示,图像与轴的一个交点是 , 对称轴是直线 , 下列结论正确的为( )
①;②;③;④)(为实数)
A、①④ B、②③④ C、①②④ D、①②③④二、填空题.
-
11. 若△ABC∽△A′B′C′,且 , △ABC的周长为12cm,则△A′B′C′的周长为.12. 已知 , 那么 .13. 在△ABC中,若 + ,则∠C的度数为.14. 已知 , ( )是一元二次方程 的两个实数根,则代数式 的值为 .15. 如图,已知传送带与水平面所成斜坡的坡度 , 如果它把物体送到离地面10米高的地方,那么物体所经过的路程为米.
 16. 若二次函数(a为常数)与x轴没有交点,则a的取值范是 .17. 如图所示,设C为反比例函数图象上一点,且长方形的面积为5,则这个反比例函数的解析式为 .
16. 若二次函数(a为常数)与x轴没有交点,则a的取值范是 .17. 如图所示,设C为反比例函数图象上一点,且长方形的面积为5,则这个反比例函数的解析式为 . 18. 如图,B是的弦, , 交于点 , 连接 , , . 若 , 则的度数是 .
18. 如图,B是的弦, , 交于点 , 连接 , , . 若 , 则的度数是 .
三、解答题.
-
19. 解方程.(1)、(2)、20. 计算 .21. 如图,为了测量出楼房的高度,从距离楼底处米的点(为水平地面)出发,沿斜面坡度为的斜坡前进30米到达点 , 在点处测得楼顶的仰角为 .
 (1)、求点到水平地面的距离.(计算结果用根号表示)(2)、求楼房的高度(参考数据: , , , , 结果精确到0.1米).22. 为提高公民法律意识,大力推进国家工作人员学法用法工作,今年暑假炎陵县教育局组织全县1350名教师参加“如法网”的法律知识考试,该县A学校参考教师的考试成绩绘制成如下统计图和统计表(满分100分,考试分数均为整数,其中最低分76分)
(1)、求点到水平地面的距离.(计算结果用根号表示)(2)、求楼房的高度(参考数据: , , , , 结果精确到0.1米).22. 为提高公民法律意识,大力推进国家工作人员学法用法工作,今年暑假炎陵县教育局组织全县1350名教师参加“如法网”的法律知识考试,该县A学校参考教师的考试成绩绘制成如下统计图和统计表(满分100分,考试分数均为整数,其中最低分76分)分数
人数
以下
10
以上
35
以上
8
 (1)、求A学校参加本次考试的教师人数;(2)、若该县各学校的基本情况一致,试估计该县参考教师本次考试成绩在分以下的人数.23. 网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/ , 每日销售量y()与销售单价x(元/)满足一次函数关系,下表记录的是有关数据,经销售发现,销售单价不低于成本价且不高于32元/ . 设公司销售板栗的日获利为w(元).
(1)、求A学校参加本次考试的教师人数;(2)、若该县各学校的基本情况一致,试估计该县参考教师本次考试成绩在分以下的人数.23. 网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/ , 每日销售量y()与销售单价x(元/)满足一次函数关系,下表记录的是有关数据,经销售发现,销售单价不低于成本价且不高于32元/ . 设公司销售板栗的日获利为w(元).x(元/)
10
11
12
y()
4000
3900
3800
(1)、求出日销售量y与销售单价x之间的函数关系式并写出自变量的取值范围;(2)、当销售单价定为多少时,销售这种板栗日获利w最大?最大利润为多少元?24. 如图,点在函数的图象上,过点M分别作x轴和y轴的平行线交函数的图象于点B、C .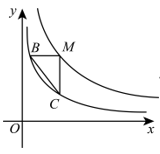 (1)、求反比例函数、直线的解析式;(2)、求的面积.
(1)、求反比例函数、直线的解析式;(2)、求的面积.