湖南省岳阳市2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、选择题（本题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 下列方程中，属于一元二次方程的是（）

A、 $3 x^{2} - 5 x = 6$ B、 $\frac{1}{x} - 2 = 0$ C、 $x^{2} + y^{2} = 4$ D、 $6 x + 1 = 0$

查看试题解析
2. 已知两非零数 $x ， y$ ，且 $3 x = 2 y$ ，则下列结论一定正确的是（）

A、 $x = 2 ， y = 3$ B、 $\frac{x}{3} = \frac{y}{2}$ C、 $\frac{x + y}{y} = \frac{5}{3}$ D、 $\frac{x + 2}{y + 3} = \frac{3}{2}$

查看试题解析
3. 反比例函数 $y = \frac{m - 5}{x}$ 的图象的每一支上， $y$ 都随 $x$ 的增大而增大，那么 $m$ 的取值范围是（）．

A、 $m < 0$ B、 $m > 0$ C、 $m < 5$ D、 $m > 5$

查看试题解析
4. 古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米2016石，验得米内夹谷，抽样取米一把，数得270粒内夹谷30粒，则这批米内夹谷约为（）

A、222石 B、224石 C、230石 D、232石

查看试题解析
5. 某企业复工之后，举行了一个简单的技工比赛，参赛的五名选手在单位时间内加工零件的合格率分别为：94.3% ，96.1% ， 94.3% ，91.7% ，93.5%.关于这组数据，下列说法正确的是（）

A、平均数是93.96% B、方差是0 C、中位数是93.5% D、众数是94.3%

查看试题解析
6. 如图，已知 $∠ D A B = ∠ C A E$ ，那么添加一个条件后，依然无法判定 $Δ A B C$ ∽ $Δ A D E$ （）

A、 $∠ A E D = ∠ C$ B、 $∠ D = ∠ B$ C、 $\frac{A B}{A D} = \frac{A C}{A E}$ D、 $\frac{A D}{A B} = \frac{D E}{B C}$

查看试题解析
7. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C D$ 是 $A B$ 边上的中线，若 $B C = 6$ ， $A C = 8$ ，则 $t a n ∠ A C D$ 的值为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析
8. 图①是一张长 $28 c m$ ，宽 $16 c m$ 的矩形纸片，将阴影部分裁去（阴影部分为4个完全相同的小矩形）并折叠成一个如图②的底面积为 $80 c m^{2}$ 的有盖长方体盒子．设该盒子的高为 $x c m$ ，根据题意，可列方程为（）

A、 $(28 - 2 x) (16 - 2 x) = 80$ B、 $(28 - 2 \times 2 x) (16 - 2 x) = 80$ C、 $(\frac{1}{2} \times 28 - 2 x) (16 - 2 x) = 80$ D、 $\frac{1}{2} (28 - 2 x) (16 - 2 x) = 80$

查看试题解析
9. 如图，A，B是反比例函数y＝ $\frac{9}{x}$ （x＞0）图象上的两点，分别过A，B两点向x轴，y轴作垂线段，AD，BE两垂线段交于点G.若图中阴影部分的面积为3，则△OAB的面积为（　　）

A、9 B、10 C、11 D、12

查看试题解析
10. 数学课上，老师让同学们以“矩形的折叠”为主题开展数学活动．如图，小明把矩形 $A B C D$ 沿 $D E$ 折叠，使点 $C$ 落在 $A B$ 边的点 $F$ 处，其中 $D E = 5 \sqrt{5}$ ，且 $s i n ∠ D F A = \frac{4}{5}$ ，则矩形 $A B C D$ 的面积为（）

A、 $80$ B、 $64$ C、 $36$ D、 $18$

查看试题解析

二、填空题（本题共6小题，每小题3分，满分18分）

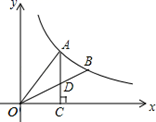
11. 在△ABC中，（cosA﹣ $\frac{1}{2}$ ）²+|tanB﹣1|＝0，则∠C＝．

查看试题解析
12. 已知点A（－1，y₁），B（－2，y₂），C（3，y₃）在反比例函数 $y = - \frac{3}{x}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系为．（用“＜”连接）

查看试题解析
13. 某件羊毛衫的售价为1000元，因换季促销，在经过连续两次降价后，现售价为810元，设平均每次降价的百分率为x，根据题意可列方程为.

查看试题解析
14. 对某班期末成绩进行统计，已知80.5～90.5分这一组的频数是10，频率是0.25，那么该班级的人数是人．

查看试题解析
15. 如图，A.B是双曲线y＝ $\frac{k}{x}$ 上的两点，过A点作AC⊥x轴，交OB于D点，垂足为C.若△ADO的面积为1，D为OB的中点，则k的值为.

查看试题解析
16. 如图， $D 、 E$ 分别是 $△ A B C$ 的边 $A B 、 B C$ 上的点， $D E ∥ A C$ ，且 $D 、 E$ 分别为 $B A 、 B C$ 边上靠近点 $B$ 的三等分点，则下列结论正确的是．
① $D E ： A C = 1 ： 3$ ；② $O D ： O C = 1 ： 2$ ；③ $S_{△ B D E} ： S_{△ C D E} = 1 ： 3$ ；④ $S_{△ D O E} ： S_{△ A O C} = 1 ： 4$

查看试题解析

三、解答题（本题共9小题，满分72分，解答应写出文字说明，证明过程或演算步骤）

17. 解方程： $| 1 - \sqrt{2} | - {(- \frac{1}{2})}^{- 2} - 2 c o s 45 ° + {(\sqrt{3} - 1)}^{0} + \sqrt[3]{8}$ ．

查看试题解析
18. 解一元二次方程：

(1)、 $x^{2} + 3 x - 4 = 0$ （用配方法）；

(2)、 $x^{2} + 2 x - 99 = 0$ （因式分解法）

查看试题解析
19. 如图，水库大坝的横断面为四边形 $A B C D$ ，其中 $A D ∥ B C$ ，坝顶 $B C = 10$ $m$ ，坝高20 $m$ ，斜坡AB的坡度 $i = 1 ： 2.5$ ，斜坡 $C D$ 的坡角为 $30 °$ ．求坝底 $A D$ 的长度（结果精确到1 $m$ ，参考数据： $\sqrt{3} \approx 1.73$ ）．

查看试题解析
20. 关于 $x$ 的一元二次方程 $x^{2} - (2 k - 1) x + k^{2} + 1 = 0$ 有两个不相等的实数根 $x_{1}$ ， $x_{2}$ .

(1)、求实数 $k$ 的取值范围；

(2)、若方程的两实数根 $x_{1}$ ， $x_{2}$ 满足 $x_{1} + x_{2} = - x_{1} \cdot x_{2}$ ，求 $k$ 的值.

查看试题解析
21. 巴川中学STEAM创新教育学部为提高学生的安全意识和安全技能，组织七、八年级学生进入区消防支队进行了实地学习和体验，并在学习结束后开展了一次消防知识竞赛．成绩分别为A、B、C、D四个等级，其中相应等级的得分依次记为10分、9分、8分、7分．学校分别从七、八年级各抽取25名学生的竞赛成绩整理并绘制成如下统计图表，请根据提供的信息解答下列问题：
年级
平均分
中位数
众数
方差
七年级
$8.76$
a
9
$1.06$
八年级
$8.76$
8
b
$1.38$

(1)、根据以上信息可以求出：a＝ ▲ ， b＝ ▲ ，并把七年级竞赛成绩统计图补充完整；

(2)、依据数据分析表，你认为七年级和八年级哪个年级的成绩更好，并说明理由；

(3)、若STEAM创新教育学部七、八年级共有800人参加本次知识竞赛，且规定9分及以上的成绩为优秀，请估计该学部七、八年级参加本次知识竞赛的学生中成绩为优秀的学生共有多少人？

查看试题解析
22. 如图， $△ A D E$ 与 $△ A B C$ 有公共顶点 $A$ ， $∠ B A D = ∠ C A E$ ．

(1)、请你写一个适当的条件，使 $△ A D E ∽ △ A B C$ ，则需添加的条件可以是 ▲ 或 ▲ ，并选择其中之一证明．

(2)、由（1）能否得出其他的相似三角形？如果能，请说明理由．

查看试题解析
23. 如图，一次函数 $y = k x + b$ 与反比例函数 $y = \frac{4}{x} (x > 0)$ 的图象交于 $A (m ， 4)$ ， $B (2 ， n)$ 两点．

(1)、求一次函数的解析式；

(2)、根据图象直接写出使 $k x + b < \frac{4}{x}$ 成立的 $x$ 的取值范围；

(3)、求 $△ A O B$ 得面积．

查看试题解析
24. 平安路上，多“盔”有你，在“交通安全宣传月”期间，某商店销售一批头盔，进价为每顶40元，售价为每顶68元，平均每周可售出100顶．商店计划将头盔降价销售，每顶售价不高于58元，经调查发现：每降价2元，平均每周可多售出40顶．设每顶头盔降价x元，平均每周的销售量为y顶．

(1)、每顶头盔降价x元后，每顶头盔的利润是元（用含x的代数式表示）；

(2)、平均每周的销售量y（顶）与降价x（元）之间的函数关系式是；

(3)、若该商店希望平均每周获得4000元的销售利润，则每顶头盔应降价多少？

查看试题解析
25.

(1)、【问题情境】如图1，小明把三角板EFG（ $∠ G F E = 30 °$ ）放置到矩形ABCD中，使得顶点E、F、G分别落在AD、CD、AB上，你发现线段ED与AG有什么数量关系？
直接写出结论：（不用证明）．

(2)、【变式探究】如图2，小明把三角板EFG（ $∠ G F E = 30 °$ ）放置到矩形ABCD中，使得顶点E、F、G分别在AD、BC、AB边上，若 $G A = 4$ ， $A E = 6$ ，求BG的长．

(3)、【拓展应用】如图3，小明把三角形EFG放置到平行四边形ABCD中，使得顶点E、F、G分别落在AD、BC、AB边上，若 $\frac{A B}{A D} = \frac{4}{5}$ ， $\frac{A E}{A D} = \frac{3}{10}$ ， $∠ F E G = ∠ B A D$ ，求出 $\frac{E G}{E F}$ 的值．

查看试题解析

年级	平均分	中位数	众数	方差
七年级	$8.76$	a	9	$1.06$
八年级	$8.76$	8	b	$1.38$