湖南省长沙市长郡教育集团联考2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、单项选择题（本大题共10小题，每小题3分，共30分）

1. 下列四个数中，最大的数是（）

A、 $- (- 2021)$ B、 $| - 2022 |$ C、 $- | - 2023 |$ D、 $- (+ 2024)$

查看试题解析
2. 2024年元旦假期的到来，点燃了消费者的出游热情，也激发了旅游市场的活力.元旦假期三天，长沙市共接待游客609.65万人次. 数据“609.65万”用科学记数法表示为（）

A、0.60965×10⁸ B、6.0965×10⁷ C、60.965×10⁶ D、6.0965×10⁶

查看试题解析
3. 单项式 $- 2 π x y^{2} z^{3}$ 的系数和次数分别是（）

A、 $- 2$ ， 6 B、 $- 2$ ， 7 C、 $- 2 π$ ， 6 D、 $- 2 π$ ， 7

查看试题解析
4. 2023年长沙国际马拉松在芙蓉中路（贺龙体育中心东广场旁）起跑，来自国内外的26000名跑友汇成一片红色的海洋驰骋在长马赛道上，他们用脚步丈量星城，感受一江两岸、山水洲城的魅力. 图①是此次全程马拉松男子组颁奖现场. 图②是领奖台的示意图，则此领奖台从正面看到的平面图形是（）

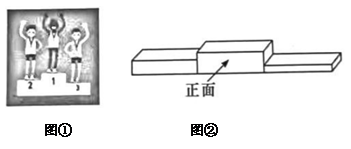A、 B、 C、 D、

查看试题解析
5. 下列变形一定正确的是（）

A、若 $a = b$ ，则 $a + c = b - c$ B、若 $\frac{a}{c} = \frac{b}{c}$ ，则 $a = b$ C、若 $2 a = 3 b$ ，则 $a = \frac{2}{3} b$ D、若 $2 a = 2 b + 1$ ，则 $a = b + 1$

查看试题解析
6. 如图，直线DE与BC相交于点O ， $∠ C O E$ 与 $∠ A O E$ 互余， $∠ B O D = 35 °$ ，则 $∠ A O E$ 的度数是（）

A、35° B、45° C、55° D、65°

查看试题解析
7. 有理数a ， b在数轴上对应点的位置如图所示，下列说法中正确的是（）

A、 $a > b$ B、 $- a > b$ C、 $| a | > | b |$ D、 $a + b > 0$

查看试题解析
8. 某学校教学楼扩建工程甲单独做9天完成，乙单独做15天完成.现在乙先做3天，甲再加入合做. 设完成此工程一共用了x天，则下列方程正确的是（）

A、 $\frac{x}{15} + \frac{x - 3}{9} = 1$ B、 $\frac{x + 3}{15} + \frac{x}{9} = 1$ C、 $\frac{x}{15} + \frac{x}{9} = 1$ D、 $\frac{x + 3}{15} + \frac{x - 3}{9} = 1$

查看试题解析
9. 如图，将一副三角尺按不同位置摆放，以下摆放方式中， $∠ α = ∠ β$ 的图形有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 1883年，德国数学家格奥尔格·康托尔用以下的方法构造了这个分形，称为康托尔集. 如图，取一条长度为1的线段，将它三等分，去掉中间一段，留剩下的两段，这称为第一阶段；然后将剩下的两段再三等分，各去掉中间一段，剩下更短的四段，这称为第二阶段，…，将这样的操作无限地重复下去，余下的线段的长度趋于0，将它们看成无穷个点，称为康托尔集，那么经过第四个阶段后，留下的线段的长度之和为（）

A、 $\frac{4}{27}$ B、 $\frac{16}{81}$ C、 $\frac{8}{243}$ D、 $\frac{16}{243}$

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

11. 计算： $9 a b - 2 a b =$ .

查看试题解析
12. 如果单项式 $- x^{m} y^{2}$ 与 $6 x y^{n + 5}$ 是同类项，那么 $m + n =$ .

查看试题解析
13. 如图，点A在点O的东南方向，点B在点O的北偏东50°方向，则∠AOB=°．

查看试题解析
14. 元旦节期间，某商店将一件衣服按成本价提高50%后标价，然后打八折卖出，结果仍获利60元，那么这件衣服的成本价是元.

查看试题解析
15. 已知 $(a - 1) x^{| a |} + 2024 = 0$ 是关于x的一元一次方程，则 $a =$ .

查看试题解析
16. 2023年5月9日，湖南湘江新区大王山欢乐云巴正式对外运营. 一张云巴票就能领略沿途10余个景点，感受大王山人文风情.如图，乘云巴从山塘站出发，沿途经过7个车站方可到达观音港站，那么运营公司在山塘站，观音港站两站之间需要安排不同的车票种.

查看试题解析

三、解答题（本大题共9小题，共22分，解答应写出文字说明，证明过程或演算步骤）

17. 解方程：

(1)、 $5 (x + 6) = 5 - 3 (1 - 3 x)$ ；

(2)、 $\frac{4 y + 2}{5} - \frac{3 y - 1}{2} = 1$ .

查看试题解析
18. 计算：

(1)、 $- 6 + (- 4) \times (- 3) + {(- 2)}^{3} \div 4$ ；

(2)、 $- 1^{3} - [2 \times (- 5) + {(- 3)}^{2}] \div \frac{1}{2}$ .

查看试题解析
19. 先化简，再求值： $- a^{2} b + 2 (3 a b^{2} - a^{2} b) - 3 (a b^{2} - a^{2} b)$ ，其中 $a = 1$ ， $b = - 2$ .

查看试题解析
20. 已知关于x的方程 $\frac{x + a}{3} = x - \frac{a}{2}$ 与方程 $3 x + 5 = 11$ 的解互为相反数，求a的值.

查看试题解析
21. 如图，线段 $A B = 24$ ， C是线段AB的中点，D是线段BC的中点.

(1)、求线段AD的长；

(2)、在线段AD上有一点E ，满足 $C E = \frac{1}{6} B C$ ，求AE的长.

查看试题解析
22. 如图，已知点O为直线AB上一点， $∠ C O E = 62 °$ ， $∠ C O D = 90 °$ ， OE平分 $∠ B O D$ .

(1)、求 $∠ A O D$ 的度数；

(2)、如图，若 $∠ A O F = 3 ∠ B O E$ ，求 $∠ F O D$ 的度数.

查看试题解析
23. 2024年10月26日，长郡中学将举行120周年华诞庆典. 为更好的展示庆典盛况，学校计划用无人机进行拍摄.选用无人机时，为比较Ⅰ号、Ⅱ号两架无人机的性能，让Ⅰ号无人机从海拔10米处出发，以18米/分钟的速度匀速上升，Ⅱ号无人机从海拔30米处同时出发，匀速上升，经过12分钟，I号无人机比Ⅱ号无人机高40米.

(1)、求Ⅱ号无人机的上升速度；

(2)、当这两架无人机位于同一海拔高度时，求此时的海拔高度.

查看试题解析
24. 定义：从一个角的顶点出发，在角的内部引两条射线如果这两条射线所成的角与这个角互余，那么这两条射线所成的角叫做这个角的内余角. 如图1，若射线OC ， OD在 $∠ A O B$ 的内部，且 $∠ C O D + ∠ A O B = 90 °$ ，则 $∠ C O D$ 是 $∠ A O B$ 的内余角.

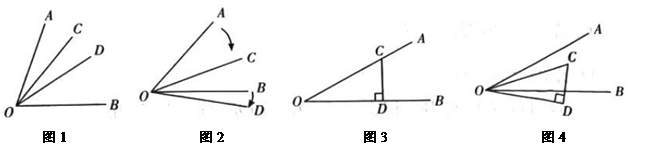
根据以上信息，解决下面的问题：

(1)、如图1， $∠ A O B = 72 °$ ， $∠ A O C = 20 °$ ，若 $∠ C O D$ 是 $∠ A O B$ 的内余角，则 $∠ B O D =$ ；

(2)、如图2，已知 $∠ A O B = 60 °$ ，将OA绕点O顺时针方向旋转一个角度 $α (0 ° < α < 60 °)$ 得到OC ，同时将OB绕点O顺时针方向旋转一个角度 $α$ 得到OD. 若 $∠ C O B$ 是 $∠ A O D$ 的内余角，求 $α$ 的值；

(3)、把一块含有30°角的三角板COD按图3方式放置，使OC边与OA边重合，OD边与OB边重合，如图4，将三角板COD绕顶点O以6度/秒的速度按顺时针方向旋转，旋转时间为t秒，在旋转一周的时间内，当射线OA ， OB ， OC ， OD构成内余角时，请求出t的值.

查看试题解析
25. 数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础.如图，在数轴上点A表示数a ，点B表示数b ，点C表示数c ，其中b是最小的正整数，且多项式 $(a + 2) x^{3} + 2 x^{2} + 9 x + 5$ 是关于x的二次多项式，一次项系数为c.

(1)、 $a =$ ， $b =$ ， $c =$ ；

(2)、若将数轴折叠，使得点A与点C重合，此时点B与某数表示的点重合，则此数为；

(3)、若这三条线段的长度之比为2∶2∶5，则折痕处对应的点在数轴上所表示的数可能是多少？

查看试题解析