湖南省岳阳市平江县2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. 2023的相反数是（）

A、 $- 2023$ B、2023 C、 $\pm 2023$ D、 $\frac{1}{2023}$

查看试题解析
2. 平江某天的最高气温是 $9 ° C$ ，最低气温是 $- 1 ° C$ ，则该地这一天的温差是（）

A、 $10 ° C$ B、 $- 8 ° C$ C、 $8 ° C$ D、 $- 10 ° C$

查看试题解析
3. 下列计算正确的是（）

A、 $x^{2} + x^{2} = x^{4}$ B、 $x^{2} + x^{3} = 2 x^{5}$ C、3x﹣2x=1 D、 $x^{2} y - 2 x^{2} y = - x^{2} y$

查看试题解析
4. 如图，数轴上的点A、B分别对应实数a、b ，下列结论中正确的是（　　）

A、a＞b B、|a|＞|b| C、﹣a＜b D、a+b＜0

查看试题解析
5. 多项式1+2xy-3xy²的次数及最高次项的系数分别是（）

A、3，-3 B、2，-3 C、5，-3 D、2，3

查看试题解析
6. 下列等式变形正确的是（）

A、如果 $x - 1 = y - 1$ ，那么 $x = y$ B、如果 $m a = m b$ ，那么 $a = b$ C、如果 $\frac{1}{3} a = b - 1$ ，那么 $a = 3 b - 1$ D、如果 $\frac{1}{2} x = 4$ ，那么 $x = \frac{1}{8}$

查看试题解析
7. 为了解某校2000名学生的视力情况，从中随机调查了400名学生的视力情况，下列说法正确的是（）

A、该调查的方式是全面调查 B、每个学生是个体 C、400名是样本容量 D、2000名学生的视力情况是总体

查看试题解析
8. 我国古代数学名著《九章算术》中记载：“今有共买物，人出八，盈三；人出七，不足四，问人数几何？”意思是现有几个人共买一件物品，每人出 $8$ 钱．多出 $3$ 钱；每人出 $7$ 钱，差 $4$ 钱．问人数是多少？若设有 $x$ 人，则可方程为（）

A、 $8 x - 3 = 7 x + 4$ B、 $8 x + 3 = 7 x - 4$ C、 $\frac{x - 3}{8} = \frac{x + 4}{7}$ D、 $\frac{x + 3}{8} = \frac{x - 4}{7}$

查看试题解析
9. 如图，一副三角尺按不同的位置摆放，摆放位置中 $∠ α = ∠ β$ 的图形是.（只填写图形编号）

查看试题解析
10. 如图，一枚棋子放在七角棋盘的第0号角，现依逆时针方向移动这枚棋子，其各步依次移动1，2，3，…， $n$ 个角，如第一步从0号角移动到第1号角，第二步从第1号角移动到第3号角，第三步从第3号角移动到第6号角，…．若这枚棋子不停地移动下去，则这枚棋子永远不能到达的角是（）

A、第2号角 B、第4号角 C、第5号角 D、第6号角

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

11. 2023年4月16日，岳阳市马拉松比赛在君山举行，共有11000人参加.11000用科学记数法表示为．

查看试题解析
12. 如果 $- 2 a^{m} b^{2}$ 与 $\frac{1}{2} a^{5} b^{n + 1}$ 是同类项，那么m+n的值为．

查看试题解析
13. 若 $x^{2} + 3 x = 7$ ，则 $3 x^{2} + 9 x + 2023$ 的值为．

查看试题解析
14. 如图，从A地到B地共有五条路，人们常常选择第③条，请用几何知识解释原因．

查看试题解析
15. 定义一种新运算“⊕”，规定有理数 $a \oplus b = 4 a b - b$ ，如： $2 \oplus 3 = 4 \times 2 \times 3 - 3 = 21$ ，根据该运算计算 $3 \oplus (- 3) =$ ．

查看试题解析
16. 一列数 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， …， $a_{n}$ ，其中 $a_{1} = - 1$ ， $a_{2} = \frac{1}{1 - a_{1}}$ ， $a_{3} = \frac{1}{1 - a_{2}}$ ， …， $a_{n} = \frac{1}{1 - a_{n - 1}}$ ，则 $a_{1} + a_{2} + a_{3} + \cdot \cdot \cdot + a_{2023} =$ ．

查看试题解析

三、解答题（本大题共9小题，8+8+6+6+6+9+9+10+10，共72分）

17. 计算：

(1)、 $- 1^{2024} - 8 \div (- 4) + 3 \times | - 2 |$ ；

(2)、 $(\frac{1}{6} - \frac{3}{4} + \frac{1}{12}) \times (- 48)$ ．

查看试题解析
18. 解方程：

(1)、 $4 x - 2 = 2 (x - 3)$ ；

(2)、 $\frac{x + 2}{4} - \frac{2 x - 3}{6} = 1$ ．

查看试题解析
19. 先化简，再求值 $(4 x^{2} - 5 x y + y^{2}) - 5 (x^{2} - x y + y^{2})$ ，其中 $| x + 1 | + (y - 2)^{2} = 0$ ．

查看试题解析
20. 若 $a$ 与 $b$ 互为相反数， $c$ 与 $d$ 互为倒数， $| e | = 5$ ，求 $(a + b)^{2023} + 4 c d - e^{2}$ 的值．

查看试题解析
21. 为有效开展阳光体育活动，云洱中学利用课外活动时间进行班级篮球比赛，每场比赛都要决出胜负，每队胜一场得2分，负一场得1分．已知九年级一班在8场比赛中得到13分，问九年级一班胜、负场数分别是多少？

查看试题解析
22. 为庆祝中国共产党建党100周年，某中学开展“学史明理、学史增信、学史崇德、学史力行”知识竞赛，现随机抽取部分学生的成绩分成A、B、C、D、E五个等级进行统计，并绘制成如下两幅不完整的统计图，请根据图中提供的信息，解答下列问题：

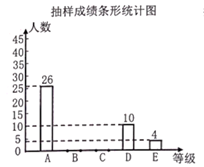
(1)、本次调查中共抽取学生；

(2)、补全条形统计图；

(3)、在扇形统计图中，求B等级所对应的扇形圆心角的度数；

(4)、若该校有1200名学生参加此次竞赛，估计这次竞赛成绩为A和B等级的学生共有多少名？

查看试题解析
23. 点 O 是直线 AB上一点，∠COD 是直角，OE平分∠BOC．

(1)、①如图1，若∠DOE＝25°，求∠AOC 的度数；
②如图2，若∠DOE＝α，直接写出∠AOC的度数（用含α的式子表示）；

(2)、将图 1中的∠COD 绕点O按顺时针方向旋转至图 2 所示位置．探究∠DOE 与∠AOC 的度数之间的关系，写出你的结论，并说明理由．

查看试题解析
24. 定义：若 $A - B = m$ ，则称 $A$ 与 $B$ 是关于 $m$ 的关联数．例如：若 $A - B = 2$ ，则称 $A$ 与 $B$ 是关于2的关联数．

(1)、若4与 $a$ 是关于7的关联数，求 $a$ 的值；

(2)、若 $2 x - 1$ 与 $3 x - 5$ 是关于6的关联数，求 $x$ 的值；

(3)、若 $M$ 与 $N$ 是关于 $m$ 的关联数， $M = 3 m n + n + 3$ ， $N$ 的值与 $m$ 无关，求 $N$ 的值．

查看试题解析
25. 如图，已知数轴上 $A$ ， $B$ ， $C$ 三个点表示的数分别是 $a$ ， $b$ ， $c$ ，且 $| c - 10 | = 0$ ，若点 $A$ 沿数轴向右移动12个单位长度后到达点 $B$ ，且点 $A$ ， $B$ 表示的数互为相反数．

(1)、 $a$ 的值为， $b - c$ 的值为；

(2)、动点 $P$ ， $Q$ 分别同时从点 $A$ ， $C$ 出发，点 $P$ 以每秒1个单位长度的速度向终点 $C$ 移动，点 $Q$ 以每秒 $m$ 个单位长度的速度向终点 $A$ 移动，点 $P$ 表示的数为 $x$ ．
①若点 $P$ ， $Q$ 在点 $B$ 处相遇，求 $m$ 的值；
②若点 $Q$ 的运动速度是点 $P$ 的2倍，当点 $P$ ， $Q$ 之间的距离为2时，求此时 $x$ 的值．

查看试题解析