湖南省永州市祁阳市2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分，每小题只有一个正确选项，请将正确选项填涂到答题卡的空格上）

1. 下列各点，一定在反比例函数 $y = \frac{3}{x}$ 图象上的是（）

A、 $(- 1 ， 3)$ B、 $(1 ， - 3)$ C、 $(- 3 ， - 1)$ D、 $(3 ， 3)$

查看试题解析
2. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A B = 5$ ， $B C = 4$ ，则 $c o s B =$ （）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{5}{3}$ D、 $\frac{3}{4}$

查看试题解析
3. 用配方法解方程 $x^{2} - 10 x - 11 = 0$ ，配方后可得（）

A、 ${(x + 5)}^{2} = 36$ B、 ${(x - 5)}^{2} = 36$ C、 ${(x - 5)}^{2} = 25$ D、 ${(x + 5)}^{2} = 25$

查看试题解析
4. 已知 $\frac{a}{b} = \frac{2}{3}$ （ $b \neq - 3$ ），则下列说法错误的是（）

A、 $2 a = 3 b$ B、 $\frac{a}{2} = \frac{b}{3}$ C、 $\frac{a + b}{b} = \frac{5}{3}$ D、 $\frac{a}{b} = \frac{a + 2}{b + 3}$

查看试题解析
5. 已知点 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2})$ 在反比例函数 $y = \frac{2}{x}$ 的图象上，且 $x_{1} < 0 < x_{2}$ ，则下列结论一定正确的是（）．

A、 $y_{1} < y_{2} < 0$ B、 $y_{1} > y_{2} > 0$ C、 $y_{1} < 0 < y_{2}$ D、 $y_{1} > 0 > y_{2}$

查看试题解析
6. 环保人员为估计某自然保护区山雀的数量，随机捕捉了100只山雀，然后在身体某部位做好标记，放回山中，隔了一段时间之后，环保人员随机捕捉了300只山雀，发现其中5只的身体上有之前做好的标记，由此可知该自然保护区山雀的数量大约为（）

A、6000只 B、3000只 C、5000只 D、8000只

查看试题解析
7. 方程 $2 x^{2} - 5 x + 3 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
8. 如图，在 $▱ A B C D$ 中，E在 $A B$ 上， $C E 、 B D$ 交于F ，若 $A B = 6 ， B E = 2$ ，且 $B F = 3$ ，则 $B D$ 的长为（）

A、 $10$ B、 $12$ C、 $14$ D、 $15$

查看试题解析
9. 反比例函数 $y = \frac{k}{x}$ 的图象如图所示， $A B ∥ y$ 轴，若 $△ A B C$ 的面积为3，则k的值为（）

A、 $\frac{1}{2}$ B、 $- \frac{3}{2}$ C、3 D、 $- 6$

查看试题解析
10. 如图，在正方形 $A B C D$ 中， $△ B P C$ 是等边三角形， $B P$ ， $C P$ 的延长线分别交 $A D$ 于点 $E$ ， $F$ ，连接 $B D$ ， $D P$ ， $B D$ 与 $C F$ 相交于点 $H$ ．给出下列结论： $① A E = \frac{1}{2} F C$ ； $② ∠ P D E = 15 °$ ； $③ \frac{S_{△ P B C}}{S_{△ P C D}} = \sqrt{3}$ ； $④ D E^{2} = P F \cdot F C$ ．其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共6小题，每小题3分，满分18分）

11. 若反比例函数 $y = \frac{1 + k}{x}$ 的图象位于第二、四象限，则k的取值范围是．

查看试题解析
12. 如图，以点O为位似中心，将△OAB放大后得到△OCD ， OA＝2，OC＝5，则 $\frac{A B}{C D}$ ＝．

查看试题解析
13. 已知一元二次方程 $x^{2} - 3 x + k = 0$ 的两个实数根为 $x_{1} ， x_{2}$ ，若 $x_{1} x_{2} + x_{1} + x_{2} = 1$ ，则实数 $k =$ ．

查看试题解析
14. 如图，传送带和地面所成斜坡的坡度 $i = 1 ∶ \sqrt{3}$ ，如果它把某物体从地面送到离地面10米高的地方，那么该物体所经过的路程是．

查看试题解析
15. 习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气．”某校为响应我市全民阅读活动，利用节假日面向社会开放学校图书馆．据统计，第一个月进馆125人次，进馆人次逐月增加，第三个月进馆405人次，若进馆人次的月平均增长率相同．进馆人次的月平均增长率是．

查看试题解析
16. 如图，n边长为1的相邻正方形的一边均在同一直线上，点 $M_{1} ， M_{2} ， M_{3} ， ⋯ M_{n}$ 为边 $B_{1} B_{2} ， B_{2} B_{3} ， B_{3} B_{4} ， ⋯ ， B_{n} B_{n + 1}$ 的中点， $△ B_{1} C_{1} M_{1}$ 的面积为 $S_{1}$ ， $△ B_{2} C_{2} M_{2}$ 的面积为 $S_{2}$ ， … $△ B_{n} C_{n} M_{n}$ 的面积为 $\frac{1}{1020}$ ，则n＝．

查看试题解析

三、解答题（本大题共9小题，满分72分，解答应写出文字说明、证明过程或演算步骤）

17. 计算： $| - \sqrt{3} | + \sqrt{2} s i n 45 ° - t a n 60 ° - {(- \frac{1}{3})}^{- 1}$ ．

查看试题解析
18. 解方程： $x^{2} - 4 x - 2 = 0$

查看试题解析
19. 如图， $A C ， B D$ 相交于点O ， $∠ A = ∠ D$ ．

(1)、求证： $△ A O B ∽ △ D O C$ ；

(2)、已知 $A O = 3 ， D O = 2$ ， $△ A O B$ 的面积为6，求 $△ D O C$ 的面积．

查看试题解析
20. 我市教育局为深入贯彻落实立德树人根本任务，2022年在全市中小学部署开展“六个一”德育行动．某校为了更好地开展此项活动，随机抽取部分学生对学校前段时间开展活动的情况进行了满意度调查，满意度分为四个等级：A：非常满意；B：满意；C：一般；D：不满意．根据调查数据绘制了如下两幅不完整的统计图表：

等级

人数

A

72

B

108

C

48

D

m

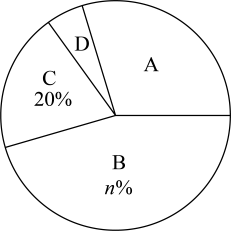
请你根据图表中的信息，解答下列问题：

(1)、本次被调查的学生人数是多少？

(2)、求以上图表中m ， n的值及扇形统计图中A等级对应的圆心角度数；

(3)、若该校共有学生1200人，估计满意度为A ， B等级的学生共有多少人？

查看试题解析
21. 已知关于 $x$ 的一元二次方程 $x^{2} - 4 x + 1 - k = 0$ ．

(1)、若这个方程没有实数根，求 $k$ 的取值范围．

(2)、当 $k = - 2$ 时，若等腰三角形的两边长分别为该方程的两个根，求这个等腰三角形的周长．

查看试题解析
22. 已知一次函数 $y = k x + b$ （ $k \neq 0$ ）与反比例函数 $y = \frac{m}{x}$ （ $m \neq 0$ ）的图象交于 $A (2 ， 3)$ ， $B (- 6 ， n)$ 两点．

(1)、求一次函数和反比例函数的解析式；

(2)、求 $△ A O B$ 的面积．

查看试题解析
23. 随着技术进步和成果转化，在我国无人机的用武之地越来越多，农林植保、应急救援、文物保护、电力巡检……，加速赋能千行百业．如图，某农业示范基地用无人机对一块试验田进行监测作业时，无人机在点A处，无人机距地面高度 $A O$ 为120米，此时测得试验田一侧边界点C处俯角为 $52 °$ ，无人机垂直下降40米至点B处，又测得试验田另一侧边界点D处俯角为 $40 °$ ，且点C ， O ， D在同一条直线上，求点C与点D的距离．（参考数据： $s i n 52 ° \approx 0.8 ， c o s 52 ° \approx 0.6 ， t a n 52 ° \approx 1.3 ， s i n 40 ° \approx 0.6 ， c o s 40 ° \approx 0.8 ， t a n 40 ° \approx 0.8$ ，结果保留整数）

查看试题解析
24. 如图，在正方形 $A B C D$ 中，点G是对角线 $B D$ 上一点， $C G$ 的延长线交 $A B$ 于点E ，交 $D A$ 的延长线于点F ，连接 $A G$ ．

(1)、求证： $C G = A G$ ；

(2)、求证： $A B^{2} = B E \cdot D F$ ；

(3)、若 $G E = \sqrt{3} ， G C = 2 \sqrt{2}$ ，求 $E F$ 的长．

查看试题解析
25. 在平面直角坐标系中，对于不在坐标轴上的任意点 $A (x ， y)$ ，我们把点B $(\frac{1}{x} ， \frac{1}{y})$ 称为点A的“倒数点”．

(1)、写出平面直角坐标系中第三象限内“倒数点”是本身的点的坐标；

(2)、点P是反比例函数 $y = \frac{\sqrt{2}}{x} (x > 0)$ 图象上的一点，求出点P的“倒数点”Q满足的函数表达式；

(3)、如图，矩形 $O C D E$ 的顶点 $C (3 ， 0)$ ，顶点E在y轴上，函数 $y = \frac{2}{x} (x > 0)$ 的图象与 $D E$ 交于点A ．若点B点A的“倒数点”，且点B在矩形 $O C D E$ 的一边上，求 $△ O B C$ 的面积．

查看试题解析

等级	人数
A	72
B	108
C	48
D	m