湖南省永州市道县2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，满分30分）

1. 若使分式 $\frac{6}{x^{2} - 9}$ 有意义，则字母x的满足的条件是（）

A、 $x = 3$ B、 $x = - 3$ C、 $x \neq 3$ 且 $x \neq - 3$ D、 $x = 3$ 或 $x = - 3$

查看试题解析
2. 下列命题是真命题的是（）

A、若 $a b > 0$ ，则 $a > 0$ ， $b > 0$ B、若 $a b < 0$ ，则 $a < 0$ ， $b < 0$ C、若 $a > b$ ，则 $a c > b c$ D、若 $a > b$ ，则 $- 5 a < - 5 b$

查看试题解析
3. 如图，为估计池塘两岸A、B间的距离，一位同学在池塘一侧选取一点P ，测得 $P A = 18 m$ ， $P B = 16 m$ ，那么A、B之间的距离不可能是（）

A、 $18 m$ B、 $16 m$ C、 $30 m$ D、 $34 m$

查看试题解析
4. 在实数1.732、 $\sqrt{5}$ 、 $- \frac{22}{7}$ 、 $- \sqrt{8}$ 、 $\frac{π}{3}$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 2023年8月29日华为公司上市的 $M a t e 60$ 手机搭载的是自主研发的麒麟9000处理器，这款处理器是华为首款采用 $5 n m$ 制程技术的手机芯片， $1 n m = 0.000000001 m$ ，其中 $0.000000005 m$ 用科学记数法表示为（）

A、 $5 \times 1 0^{9} m$ B、 $0.5 \times 1 0^{- 10} m$ C、 $5 \times 1 0^{- 8} m$ D、 $5 \times 1 0^{- 9} m$

查看试题解析
6. 如图，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带上（）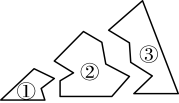

A、① B、② C、③ D、①和③

查看试题解析
7. 下列说法正确的是（）

A、9的平方根是3 B、36的算术平方根是6 C、 $\sqrt{49}$ 的平方根是 $\pm 7$ D、 $- 25$ 的算术平方根是5

查看试题解析
8. 若 $a$ ， $b$ 为实数，且 $| a + 2 | + \sqrt{b - \frac{1}{2}} = 0$ ，则 ${(a b)}^{2024}$ 的值为（）

A、0 B、1 C、 $- 1$ D、 $\pm 1$

查看试题解析
9. 下列计算正确的是（）

A、 $\sqrt{(- 11)^{2}} = - 11$ B、 $3 \sqrt{2} - 2 \sqrt{2} = 1$ C、 $\sqrt{3} + \sqrt{7} = \sqrt{10}$ D、 $5 \times \sqrt{\frac{1}{5}} = \sqrt{5}$

查看试题解析
10. 如图，在 $△ A B C$ 中， $P A$ 平分 $∠ B A C$ 交 $B C$ 于点 $P$ ，作 $P R ⊥ A B$ ， $P S ⊥ A C$ ，垂足分别为 $R$ 、 $S$ ，若 $A Q = P Q$ ，则下列四个结论：① $P R = P S$ ；② $A S = A R$ ；③ $Q P ∥ A R$ ；④ $△ B R P ≌ △ C S P$ ．其中结论正确的序号有（）

A、①②③ B、②③④ C、①③④ D、①②③④

查看试题解析

二、填空题（本大题共6小题，每小题3分，满分18分）

11. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值等于0，则x的值为

查看试题解析
12. 若一个正数的两个平方根是 $2 x - 2$ 和 $- 3 x + 6$ ，则 $x - 12$ 的立方根为．

查看试题解析
13. 已知3^m=8，3ⁿ=2，则3^m⁺ⁿ= ．

查看试题解析
14. 关于x的不等式组 ${\begin{array}{l} a - x > 3 ， \\ 2 x + 8 > 4 a \end{array}$ 无解，则a的取值范围是．

查看试题解析
15. 如图，已知 $A B = A_{1} B$ ， $A_{1} B_{1} = A_{1} A_{2}$ ， $A_{2} B_{2} = A_{2} A_{3}$ ， $A_{3} B_{3} = A_{3} A_{4} \cdot \cdot \cdot$ ，若 $∠ A = 80 °$ ，则 $∠ B_{3} A_{4} A_{3}$ 的度数为．

查看试题解析
16. 阅读与计算：阅读以下材料，并完成相应的任务：斐波那契（约1170～1250）是意大利数学家，他研究了一列数，这列数非常奇妙，被称为斐波那契数列（按照一定顺序排列着的一列数称为数列），后来人们研究它的过程中，发现了许多意想不到的结果，在实际生活中，很多花朵（如梅花、飞燕草、万寿菊等）的瓣数恰好是斐波那契数列中的数，斐波那契数列还有很多有趣的性质，在实际生活中也有广泛的应用．
斐波那契数列中的第 $n$ 个数可以用 $\frac{1}{\sqrt{5}} [{(\frac{1 + \sqrt{5}}{2})}^{n} - {(\frac{1 - \sqrt{5}}{2})}^{n}]$ 表示（其中 $n \geq 1$ ），这是用无理数表示有理数的一个范例，请计算斐波那契数列中的第2个数的值是．

查看试题解析

三、解答题（本大题共9小题，满分72分，第17、18、19题每题6分，第20、21题每题8分，第22、23每题9分，第24、25题每题10分．解答题要写出必要的文字说明、证明过程或演算步骤）

17. 先化简，再求值．
$(1 - \frac{1}{x + 1}) \div \frac{x^{2}}{x^{2} - 1}$ ，其中 $x = - 2023$ ．

查看试题解析
18. 解下列一元一次不等式组，并把它们的解集在数轴上表示出来．
${\begin{array}{l} \frac{x + 2}{3} - \frac{x - 1}{2} > 1 ① \\ 3 (4 x + 2) \geq 2 (2 x - 5) ② \end{array}$

查看试题解析
19. 解分式方程．

(1)、 $\frac{3}{x - 2} = 2 + \frac{x}{2 - x}$

(2)、 $\frac{2}{x + 1} - \frac{3}{1 - x} = \frac{6}{x^{2} - 1}$

查看试题解析
20. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点 $D$ ， $E F$ 垂直平分 $A C$ ，交 $A C$ 于点 $F$ ，交 $B C$ 于点 $E$ ，连接 $A E$ ，且 $A B = C E$ ．

(1)、求证： $A D$ 平分 $∠ B A E$ ．

(2)、若 $∠ B A E = 50 °$ ，求 $∠ C$ 的度数．

查看试题解析
21. 已知 $a$ 的平方根是 $\pm 2$ ， $b$ 是27的立方根， $c$ 是 $\sqrt{12}$ 的整数部分．

(1)、求 $a + b + c$ 的值；

(2)、若 $x$ 是 $\sqrt{12}$ 的小数部分，求 $x - \sqrt{12} + 21$ 的平方根．

查看试题解析
22. 如图①，油纸伞是中国传统工艺品之一，起源于中国的一种纸制或布制伞．油纸伞的制作工艺十分巧妙，如图②，伞圈D沿着伞柄 $A P$ 滑动时，伞柄 $A P$ 始终平分同一平面内两条伞骨所成的 $∠ B A C$ ，伞骨 $B D$ ， $C D$ 的B ， C点固定不动，且到点A的距离 $A B = A C$ ．

(1)、当D点在伞柄 $A P$ 上滑动时，处于同一平面的两条伞骨 $B D$ 和 $C D$ 相等吗？请说明理由．

(2)、如图③，当油纸伞撑开时，伞的边缘M ， N与点D在同一直线上，若 $∠ B A C = 140 °$ ， $∠ M B D = 120 °$ ，求 $∠ C D A$ 的度数．

查看试题解析
23. “走，去永州，品道州脐橙”，道州脐橙果大形正，橙红鲜艳，肉质脆嫩化渣，风味浓甜芳香.2023年11月29日在“道州脐橙”品牌推介活动上，某水果批发商用40000元购进一批道州脐橙后，供不应求，该水果批发商又用90000元购进第二批这种道州脐橙，所购数量是第一批数量的2倍，但每箱贵了10元

(1)、有水果批发商购进的第一批道州脐橙每箱多少元？

(2)、若两次购进的道州脐橙按同一价格售出，两批脐橙全部销售完后，获利不低于17000元，则销售单价至少是多少元？

查看试题解析
24. 观察下列式子的变形过程，然后回答问题：
例1： $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \frac{\sqrt{2} - 1}{(\sqrt{2})^{2} - 1} = \frac{\sqrt{2} - 1}{1} = \sqrt{2} - 1$ ．
例2： $\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}$ ， $\frac{1}{\sqrt{4} + \sqrt{3}} = \sqrt{4} - \sqrt{3}$ ， $\frac{1}{\sqrt{5} + \sqrt{4}} = \sqrt{5} - \sqrt{4}$
利用以上结论解答以下问题：

(1)、观察上面式子的变形，请直接写出 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ （ $n$ 为正整数）的结果是．

(2)、应用上面的结论，求下列式子的值．
$\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \frac{1}{\sqrt{5} + \sqrt{4}} + \dots + \frac{1}{\sqrt{100} + \sqrt{99}}$

(3)、拓展提高，求下列式子的值， $\frac{1}{1 + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{5}} + \frac{1}{\sqrt{5} + \sqrt{7}} + \dots + \frac{1}{\sqrt{2021} + \sqrt{2023}}$ ．

查看试题解析
25. 在直线m上依次取互不重合的三个点D ， A ， E ，在直线m上方有 $A B = A C$ ，且满足 $∠ B D A = ∠ A E C = ∠ B A C = α$ ．

(1)、【积累经验】
如图1，当 $α = 90 °$ 时，猜想线段DE ， BD ， CE之间的数量关系是；

(2)、【类比迁移】
如将2，当 $0 < α < 180 °$ 时，问题（1）中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由；

(3)、【拓展应用】
如图3，在 $△ A B C$ 中， $∠ B A C$ 是钝角， $A B = A C$ ， $∠ B A D < ∠ C A E$ ， $∠ B D A = ∠ A E C = ∠ B A C$ ，直线m与CB的延长线交于点F ，若 $B C = 3 F B$ ， $△ A B C$ 的面积是12，请直接写出 $△ F B D$ 与 $△ A C E$ 的面积之和．

查看试题解析