湖南省长沙市望城区2023-2024学年八年级上学期期末数学试卷
试卷更新日期:2024-03-13 类型:期末考试
一、选择题(共10小题)
-
1. 若 , 那么k的值是( )A、 B、 C、6 D、2. 使分式有意义的x的取值范围是( )A、 B、 C、 D、3. 在下列交通标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 以下列数值为长度的各组线段中,能组成三角形的是( )A、2,4,7 B、3,3,6 C、5,8,2 D、4,5,65. 分解因式 结果正确的是( )A、 B、 C、 D、6. 下列各式: , 其中分式有( )A、1个 B、2个 C、3个 D、4个7. 如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是( )
4. 以下列数值为长度的各组线段中,能组成三角形的是( )A、2,4,7 B、3,3,6 C、5,8,2 D、4,5,65. 分解因式 结果正确的是( )A、 B、 C、 D、6. 下列各式: , 其中分式有( )A、1个 B、2个 C、3个 D、4个7. 如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是( )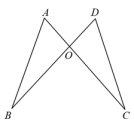 A、SSS B、SAS C、AAS D、HL8. 如图,是等边的边上的高,以点为圆心,长为半径作弧交的延长线于点 , 则( )
A、SSS B、SAS C、AAS D、HL8. 如图,是等边的边上的高,以点为圆心,长为半径作弧交的延长线于点 , 则( ) A、 B、 C、 D、9. 已知 , 则的值等于( )A、6 B、 C、12 D、10. 若一个正整数能表示为两个连续奇数的平方差,则称这个正整数为“好数”.下列正整数中能称为“好数”的是( )A、205 B、250 C、502 D、520
A、 B、 C、 D、9. 已知 , 则的值等于( )A、6 B、 C、12 D、10. 若一个正整数能表示为两个连续奇数的平方差,则称这个正整数为“好数”.下列正整数中能称为“好数”的是( )A、205 B、250 C、502 D、520二、填空题(共6小题)
-
11. 已知一个多边形的内角和为540°,则这个多边形是边形.12. 因式分解 .13. 若 , 则的值为 .14. 已知三角形的三边长分别是3、4、x , 则x的取值范围是 .15. 如图,以△ABC的顶点B为圆心,BA长为半径画弧,交于点 , 连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为度.
 16. 已知 , , , 则代数式的值是 .
16. 已知 , , , 则代数式的值是 .三、解答题(共9小题)
-
17. 因式分解:(1)、;(2)、 .18. 如图,在五边形ABCDE中, , 求x的值.
 19. 如图,在△ABC中,BO平分∠ABC , CO平分∠ACB , 过点O作BC的平行线与AB , AC分别相交于点M , N . 若AB=5,AC=6,求△AMN的周长.
19. 如图,在△ABC中,BO平分∠ABC , CO平分∠ACB , 过点O作BC的平行线与AB , AC分别相交于点M , N . 若AB=5,AC=6,求△AMN的周长.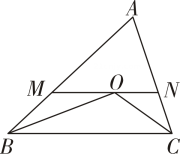 20. 规定 , 求:(1)、求;(2)、若 , 求x的值.21. 计算或解方程:(1)、计算:(2)、解方程: .22. 计算(1)、;(2)、;(3)、 .23. 甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家出发去学校,结果甲同学比乙同学早到2分钟.
20. 规定 , 求:(1)、求;(2)、若 , 求x的值.21. 计算或解方程:(1)、计算:(2)、解方程: .22. 计算(1)、;(2)、;(3)、 .23. 甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家出发去学校,结果甲同学比乙同学早到2分钟.
(1)、求乙骑自行车的速度;(2)、当甲到达学校时,乙同学离学校还有多远?

