湖南省长沙市芙蓉区2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-03-13 类型:期末考试
一、选择题(共10小题)
-
1. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性,下列美术字是轴对称图形的是( )A、诚 B、信 C、友 D、善2. 要使分式有意义,则的取值应满足( )A、 B、 C、 D、3. 点关于y轴对称的点的坐标是( )A、 B、 C、 D、4. 下列各式由左边到右边的变形中,是因式分解的是( )A、 B、 C、 D、5. 下列计算正确的是( )A、a8 ÷ a2=a4 B、a3·a4=a7 C、(2a2)3=6a6 D、( )-2=6. 下列各式中,正确的是( )A、 B、 C、 D、7. 与的边重合, . 添加下一个条件后,仍无法判定的是( )
 A、 B、 C、 D、8. 如图,在中, , 的垂直平分线交于点 , 交于点 , 连接 , 若 , 则的度数为( )
A、 B、 C、 D、8. 如图,在中, , 的垂直平分线交于点 , 交于点 , 连接 , 若 , 则的度数为( ) A、25° B、30° C、35° D、50°9. 如图,在 中, 平分 , , ,则 的长为( )
A、25° B、30° C、35° D、50°9. 如图,在 中, 平分 , , ,则 的长为( ) A、3 B、11 C、15 D、910. 关于 的方程 的两个解为 ; 的两个解为 ; 的两个解为 ,则关于 的方程 的两个解为( )A、 B、 C、 D、
A、3 B、11 C、15 D、910. 关于 的方程 的两个解为 ; 的两个解为 ; 的两个解为 ,则关于 的方程 的两个解为( )A、 B、 C、 D、二、填空题(共6小题)
-
11. 计算: .12. 数0.0000046用科学记数法表示为: .13. 已知 , 则的值为 .14. 我国古代著作《增删算法统宗》中记载了一首古算诗:“林下牧童闹如簇,不知人数不知竹每人六竿多十四,每人八竿恰齐足”其大意是:“牧童们在树下拿着竹竿高兴地玩耍,不知与多少人和竹竿每人6竿,多14竿;每人8竿,恰好用完”若设有牧童x人,根据题意,可列方程为 .15. 已知a+b=5,ab=3, = .16. 如图,在中, , 点和点在直线的同侧, , 连接 , 则的度数为 .
三、解答题(共9小题)
-
17. 计算18. 分解因式:(1)、;(2)、19. 先化简,再求值: , 其中 .20. 解分式方程(1)、(2)、 .21. 如图,在平面直角坐标系中,点A(-3,0),点B(-1,5).
 (1)、①画出线段AB关于y轴对称的线段CD;
(1)、①画出线段AB关于y轴对称的线段CD;②在y轴上找一点P使PA+PB的值最小(保留作图痕迹);
(2)、按下列步骤,用不带刻度的直尺在线段CD找一点Q使∠BAQ=45°.①在图中取点E , 使得BE=BA , 且BE⊥BA , 则点E的坐标为 ▲ ;
②连接AE交CD于点Q , 则点Q即为所求.
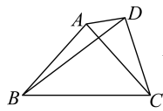
22. 已知,在中, , , , , 垂足分别为点 , . (1)、如图 , 求证:;(2)、如图 , 点为的中点,连接 , 请判断的形状?并说明理由.23. “军运会”期间,某纪念品店老板用5000元购进一批纪念品,由于深受顾客喜爱,很快售完,老板又用6000元购进同样数目的这种纪念品,但第二次每个进价比第一次每个进价多了2元.(1)、求该纪念品第一次每个进价是多少元?(2)、老板以每个15元的价格销售该纪念品,当第二次纪念品售出时,出现了滞销,于是决定降价促销,若要使第二次的销售利润不低于900元,剩余的纪念品每个售价至少要多少元?24. 如图,在四边形中,所在的直线垂直平分线段 , 过点作交于 , 延长、交于点 .
(1)、如图 , 求证:;(2)、如图 , 点为的中点,连接 , 请判断的形状?并说明理由.23. “军运会”期间,某纪念品店老板用5000元购进一批纪念品,由于深受顾客喜爱,很快售完,老板又用6000元购进同样数目的这种纪念品,但第二次每个进价比第一次每个进价多了2元.(1)、求该纪念品第一次每个进价是多少元?(2)、老板以每个15元的价格销售该纪念品,当第二次纪念品售出时,出现了滞销,于是决定降价促销,若要使第二次的销售利润不低于900元,剩余的纪念品每个售价至少要多少元?24. 如图,在四边形中,所在的直线垂直平分线段 , 过点作交于 , 延长、交于点 . (1)、求证:平分;(2)、求证:;(3)、若 , , 的面积为求的长.25. 阅读下面材料并解决有关问题:
(1)、求证:平分;(2)、求证:;(3)、若 , , 的面积为求的长.25. 阅读下面材料并解决有关问题:(一)由于 , 所以 , 即 , 并且当时,;对于两个非负实数 , , 由于所以 , 即 , 所以 , 并且当时,;
(二)分式和分数有着很多的相似点,如类比分数的基本性质,我们得到了分式的基本性质.小学里,把分子比分母小的数叫做真分数,类似的,我们把分子的次数小于分母的次数的分式称为真分式,反之,称为假分式.对于任何一个假分式都可以化成整式与真分式的和的形式,如:;
(1)、在①、②、③、④这些分式中,属于假分式的是(填序号);(2)、已知: , 求代数式的值;(3)、当为何值时,有最小值?并求出最小值.(写出解答过程)