四川省成都市郫都区2023-2024学年八年级上学期期末数学试卷
试卷更新日期:2024-03-13 类型:期末考试
一、选择题:本题共8小题,每小题4分,共32分。
-
1. 的值为( )A、± 3 B、3 C、-3 D、92. 要使二次根式有意义,则的值不可以为( )A、 B、 C、 D、3. 平面直角坐标系中,点(-1,3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 二元一次方程的一个解是( )A、 B、 C、 D、5. 下列选项中,可以用来证明命题“若 , 则”是假命题的反例是( )A、 B、 C、 D、6. 我国民间流传着许多趣味算题,他们多以顺口溜的形式表达,其中孙子算经中记载了这样一个数学问题:一群老头去赶集,半路买了一堆梨,一人一个多一梨,一人两个少二梨,请问君子知道否,几个老头几个梨?若设有个老头,个梨,则可列方程组为( )A、 B、 C、 D、7. 如图,一次函数的图象与轴交于点 , 与轴交于点 , 下列结论正确的是( )
 A、当时, B、当时, C、当时, D、当时,8. 如图,显示某滑雪俱乐部甲、乙两组各六名会员的身高情况,则下列说法错误的是( )
A、当时, B、当时, C、当时, D、当时,8. 如图,显示某滑雪俱乐部甲、乙两组各六名会员的身高情况,则下列说法错误的是( ) A、甲组的极差为 B、甲组的众数为 C、乙组的中位数为 D、甲组的方差小于乙组的方差
A、甲组的极差为 B、甲组的众数为 C、乙组的中位数为 D、甲组的方差小于乙组的方差二、填空题:本题共10小题,每小题4分,共40分。
-
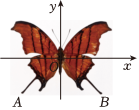
9. 如图,将一只蝴蝶标本放在平面直角坐标系中,若点的坐标为 , 则其关于轴对称的点的坐标为 .
 10. 若一次函数是正比例函数,则的值为 .11. 如图,中, , 过点作若 , 则的大小为 .
10. 若一次函数是正比例函数,则的值为 .11. 如图,中, , 过点作若 , 则的大小为 .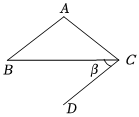 12. 化简: .13. 如图,在中, , 按以下步骤作图:分别以点、为圆心,以大于的长为半径作弧,两弧相交于两点、;作直线交于点 , 连接若 , 则的周长为 .
12. 化简: .13. 如图,在中, , 按以下步骤作图:分别以点、为圆心,以大于的长为半径作弧,两弧相交于两点、;作直线交于点 , 连接若 , 则的周长为 . 14. 如图,在数轴上点 A 表示的实数是 .
14. 如图,在数轴上点 A 表示的实数是 . 15. 若 , 则的值为 .16. 已知、、满足 , 则:: .17. 如图,在平面直角坐标系中,图案由全等的个长方形纸片摆成的若点 , 则点的坐标为 .
15. 若 , 则的值为 .16. 已知、、满足 , 则:: .17. 如图,在平面直角坐标系中,图案由全等的个长方形纸片摆成的若点 , 则点的坐标为 .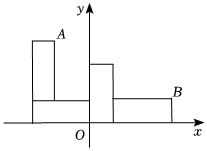 18. 如图,中, , 且 , 以为边在外部作等边点 , 连接 , 则的长为 .
18. 如图,中, , 且 , 以为边在外部作等边点 , 连接 , 则的长为 .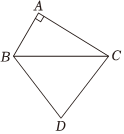
三、解答题:本题共8小题,共78分。
-
19. 计算:(1)、;(2)、 .20. 按要求解方程组,题用代入法,题用加减法:(1)、(2)、 .21. 某校组织了一次“校徽设计“竞赛活动,邀请名老师作为专业评委,名学生代表参与民主测评,且民主测评的结果无弃权票.某作品的评比数据统计如下:

专业评委
给分单位:分
专业评委给分统计表
记“专业评委给分”的平均数为 .
(1)、求该作品在民主测评中得到“不赞成”的票数;(2)、对于该作品,问的值是多少?(3)、记“民主测评得分”为 , “综合得分”为 , 若规定:“赞成”的票数分“不赞成”的票数分;
.
求该作品的“综合得分”的值.
22. 在中, , 点在内,连接、 , 延长到点 , 使得延长到点 , 使得 , 连接、完成下列问题的证明,要求这写出每步的推导理由. (1)、求证:;(2)、连接 , 延长交于 , 连接若 , 求证: .23. 如图,在平面直角坐标系中,一次函数的图象与轴、轴相交于、两点,点在线段上,以为直角边作等腰直角 , , 点恰好落在直线上.
(1)、求证:;(2)、连接 , 延长交于 , 连接若 , 求证: .23. 如图,在平面直角坐标系中,一次函数的图象与轴、轴相交于、两点,点在线段上,以为直角边作等腰直角 , , 点恰好落在直线上. (1)、求、的值;(2)、求点的坐标;(3)、若将沿直线翻折到直角坐标系平面得 , 求过点且与直线平行的直线的解析式.24. 某商场投入资金购进甲、乙两种矿泉水共箱,矿泉水的进价与售价单位:元箱如下表:
(1)、求、的值;(2)、求点的坐标;(3)、若将沿直线翻折到直角坐标系平面得 , 求过点且与直线平行的直线的解析式.24. 某商场投入资金购进甲、乙两种矿泉水共箱,矿泉水的进价与售价单位:元箱如下表:矿泉水类别
进价元箱
售价元箱
甲
乙
(1)、若该商场为购进甲、乙两种矿泉水共用元,则该商场购进甲、乙两种矿泉水各多少箱?(2)、若设购进甲种矿泉水箱,甲、乙两种矿泉水全部售完后商场共获得利润为元直接写出与之间的函数关系式.25. 对于平面直角坐标系中的点、 , 给出如下定义:若、为某个三角形的顶点,且边上的高 , 满足 , 则称该三角形为点、的“等值三角形”,已知点 . (1)、若点 , 点在的正半轴上,且是点、的“等值三角形”,求的坐标;(2)、若以线段为底的等腰三角形是点、的“等值三角形”,求该三角形的腰长;(3)、若是点、的“等值三角形”,且点在轴上,点在直线上,求点的坐标.26. 如图,在四边形中,是四边形的对角线, , , 且 .
(1)、若点 , 点在的正半轴上,且是点、的“等值三角形”,求的坐标;(2)、若以线段为底的等腰三角形是点、的“等值三角形”,求该三角形的腰长;(3)、若是点、的“等值三角形”,且点在轴上,点在直线上,求点的坐标.26. 如图,在四边形中,是四边形的对角线, , , 且 . (1)、如图 , 求证:平分;(2)、如图 , 若 , 求的度数;(3)、如图 , 延长、相交于点 , 再过点作射线交的延长线于点若 , 求证: .
(1)、如图 , 求证:平分;(2)、如图 , 若 , 求的度数;(3)、如图 , 延长、相交于点 , 再过点作射线交的延长线于点若 , 求证: .