贵州省遵义市2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-03-13 类型：期末考试

进入出卷网下载

一、选择题（本题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的，请用2B铅笔把答题卡上对应题目的答案标号涂黑、涂满．）

1. -5 的绝对值是（）

A、-5 B、 $- \frac{1}{5}$ C、5 D、 $\frac{1}{5}$

查看试题解析
2. 如图是正方体的展开图，把展开图还原为正方体后，“拼”字一面相对面上的字是（）
爱
拼
才

会
赢
！

A、爱 B、会 C、赢 D、！

查看试题解析
3. 某超市苹果的单价为a元/千克，香蕉的单价为b元/千克，小明买2千克苹果和3千克香蕉共需（）

A、 $(a + b)$ 元 B、 $(3 a + 2 b)$ 元 C、 $5 (a + b)$ 元 D、 $(2 a + 3 b)$ 元

查看试题解析
4. 关于x的一元一次方程 $3 x + m = - 2$ 的解为 $x = 1$ ，则m的值为（）

A、4 B、－5 C、1 D、－1

查看试题解析
5. “好山好水迎贵客，最美遵义人气旺”，2023年中秋、国庆假期，遵义市累计接待游客654万人次，这个数用科学记数法表示正确的是（）

A、 $0.654 \times 1 0^{7}$ B、 $65.4 \times 1 0^{5}$ C、 $6.54 \times 1 0^{6}$ D、 $6.54 \times 1 0^{7}$

查看试题解析
6. 下列计算正确的是（）

A、 $3 x y - 4 x y = - 1$ B、 $3 m + 4 n = 7 m n$ C、 $x^{2} y + 3 y = 3 x^{2} y^{2}$ D、 $5 m^{2} - 2 m^{2} = 3 m^{2}$

查看试题解析
7. 已知a、b为有理数，现规定一种新运算“※”，满足 $a ※ b = 3 b - a b$ ，若 $x ※ 2 = 2$ ，则x的值为（）

A、－4 B、－2 C、2 D、 $\frac{1}{2}$

查看试题解析
8. 如图，将正方形纸片ABCD的 $∠ E C F$ 沿着EF折叠（点E在BC上，不与B ， C重合），使点C落在正方形内部点G处，若EA平分 $∠ B E G$ ， $∠ E F C = 58 °$ ，则 $∠ B A E$ 的度数是（）

A、32° B、34° C、58° D、30°

查看试题解析
9. 《九章算术》中有如下问题：“以绳测井，若将绳三折测之，绳多四尺；若将绳四折测之，绳多一尺．问绳长、井深各几何？”其题意是：用绳子测量水井深度，如果将绳子折成三等份，那么每等份绳长比水井深度多四尺；如果将绳子折成四等份，那么每等份绳长比水井深度多一尺．问绳长和井深各多少尺？设绳长为x尺，则根据题意，可列方程为（）

A、 $\frac{x}{3} + 4 = \frac{x}{4} + 1$ B、 $\frac{x}{3} - 4 = \frac{x}{4} - 1$ C、 $\frac{x}{3} - 1 = \frac{x}{4} - 4$ D、 $\frac{x}{3} - 4 = \frac{x}{4} + 1$

查看试题解析
10. 已知线段 $A B = 24$ ，点C为线段AB的中点，点D为线段AC上的三等分点，则线段BD的长的最大值为（）

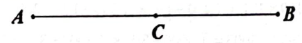A、16 B、18 C、15 D、20

查看试题解析
11. 若x、y二者满足等式 $x^{2} - 3 y = 3 x + y^{2}$ ，且x、y互为倒数，则代数式 $x^{2} - 3 (x + y) + 5 - y^{2} - 4 x y$ 的值为（）

A、1 B、4 C、5 D、9

查看试题解析
12. 正方形ABCD在数轴上的位置如图，点A、B对应的数分别为－1和0，若正方形ABCD绕顶点沿顺时针方向在数轴上连续翻转，翻转1次后，点C所对应的数为1，则连续翻转2024次后，则数2024对应的点为（）

A、点A B、点B C、点C D、点D

查看试题解析

二、填空题（本题共4小题，每小题4分，共16分．答题请用黑色墨水笔或黑色签字笔直接答在答题卡的相应位置上．）

13. 我们把零上3℃记为“＋3”℃，则零下7℃记为℃．

查看试题解析
14. 如图，某同学的家在P处，他想尽快赶到附近C处搭顺风车．他选择了第②条路线，这其中蕴含的数学道理是．

查看试题解析
15. 图1是生活中的日历，小丽同学用下列形状（图2）覆盖日历中的5个数字，若覆盖的5个数字之和为106，则A表示的数是．

查看试题解析
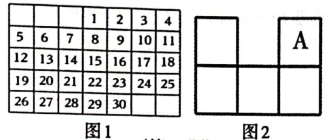16. 如图，正方形ABCD的周长为80米，甲、乙两人分别从A、B同时出发，沿正方形的边行走，甲按 $A \to B \to C \to D \to A \to B$ 这样的方向每分钟行50米，乙按 $B \to A \to D \to C \to B \to A$ 这样的方向每分钟行40米．如果用记号 $(m ， n)$ 表示两人行了m分钟，并相遇过n次，那么当两人出发后第一次处在正方形的两个相对顶点位置时，对应的记号应是．

查看试题解析

三、解答题（本题共9小题，共98分．答题请用0.5毫米黑色墨水笔签字笔或钢笔写在答题卡的相应位置上．解答时应写出必要的文字说明，证明过程或演算步骤．）

17. 计算：

(1)、 $19 - (+ 23) - (- 9) + (- 7)$

(2)、 $- 3^{2} \times (- 4) - 2^{4} \div {(- \frac{2}{3})}^{2}$

查看试题解析
18. （解方程）

(1)、 $5 x + 4 = - 2 x - 10$

(2)、小斌同学解一元一次方程 $\frac{x - 1}{2} = 3 - \frac{2 x + 1}{3}$ 的过程如下：
解： $\frac{x - 1}{2} \times 6 = 3 \times 6 - \frac{2 x + 1}{3} \times 6$ …第①步
$3 (x - 1) = 18 - 2 (2 x + 1)$ …第②步
$3 x - 1 = 18 - 4 x + 2$ …第③步
$3 x + 4 x = 18 + 2 + 1$ …第④步
$7 x = 21$ …第⑤步
$x = 3$ …第⑥步
请你指出小斌从第（_▲_）步开始出现错误，并写出完整的解题过程．

查看试题解析
19. 如图，已知A、B、C三点．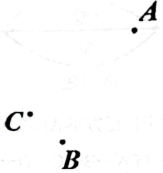

(1)、用直尺和圆规完成作图．（保留作图痕迹）

(2)、在（1）的条件下，若线段 $B C = 4 c m$ ，且 $A C = 3 B C$ ，求线段BD的长．

查看试题解析
20. 遵义市足球联赛中，由于两队水平相当，根据场上攻守形势，守门员会在门前来回跑动，如果以球门线为基准，向前跑记作正数，返回跑记作负数．一段时间内，某守门员的跑动情况记录如下（单位：m）：＋8，－3，＋5，－6，＋10，－8，＋4，－9．（假定开始计时时，守门员正好在球门线上）

(1)、守门员最后是否回到球门线上？

(2)、守门员离开球门线的最远距离达多少米？

(3)、如果守门员离开球门线的距离超过10米（包括10米），则对方球员挑射极可能造成破门．请问在这一时间段内，对方球员有几次挑射破门的机会？通过计算说明．

查看试题解析
21. 已知多项式 $A = a^{2} + 2 a b - 3 b^{2}$ ， $B = 3 a^{2} + 5 a b - 6 b^{2}$ ．

(1)、求 $A + B$ ；

(2)、若a ， b为有理数，且满足 $| a - 1 | + {(b + 2)}^{2} = 0$ 时，求 $3 A - B$ 的值．

查看试题解析
22. 2023年12月第六届遵义羊肉粉美食文化旅游节在遵义凤凰山文化广场举行，某袋装羊肉销售铺从厂家购进了甲、乙两种袋装羊肉，甲种袋装羊肉的每袋进价比乙种袋装羊肉的每件进价少15元．若购进甲种袋装羊肉7袋，乙种袋装羊肉5袋，需要795元．

(1)、求甲、乙两种袋装羊肉的每袋进价分别是多少元？

(2)、该袋装羊肉销售铺从厂家购进了甲、乙两种袋装羊肉各45袋．在销售时，甲种袋装羊肉的每袋售价为75元，乙种袋装羊肉的每袋售价为100元，在实际销售过程中，商店按售价将购进的全部甲种袋装羊肉和部分乙种袋装羊肉售出后，决定将剩下的乙种袋装羊肉打九折销售，两种袋装羊肉全部销售完后，共获利1580元，求乙种袋装羊肉打折之前销售了多少袋？

查看试题解析
23. （材料阅读）小刚的家庭作业其中一道题要用计算器计算：
① $19 \times 21$ ；② $199 \times 201$ ；③ $2997 \times 3003$ ；
但小刚身边并没有计算器，并且直接计算量大．通过思考，他发现可以巧用乘法分配律： $\begin{array}{l} a b + a c = a (b + c) \\ a (b + c) = a b + a c \end{array}$ ，按如下解法去完成：
① $19 \times 21 = (20 - 1) \times (20 + 1) = 20 \times (20 - 1) + 1 \times (20 - 1)$ $= 20 \times 20 - 20 \times 1 + 1 \times 20 - 1 \times 1 = 2 0^{2} - 1^{2} = 399$
② $199 \times 201 = (200 - 1) \times (200 + 1) = 200 \times (200 - 1) + 1 \times (200 - 1) = 20 0^{2} - 1^{2} = 39999$
③ $2997 \times 3003 = (3000 - 3) \times (3000 + 3) = 300 0^{2} - 3^{2} = 8999991$
观察上述解法，你能发现什么规律．

(1)、【问题解决】
用你发现的规律直接写出 $78 \times 82 =$ ．

(2)、【拓展探究】
请你用含字母a、b的等式表示你发现的规律：．

(3)、【拓展延伸】
下图将一个边长为a的正方形ABCD分割成一个边长为b的正方形和两个长方形，根据你上述观察规律，判断你发现的规律是否正确，若正确，写出过程，如不正确，请说明理由．

查看试题解析
24. 请根据图示的对话解答下列问题．

(1)、 $a =$ ； $b =$ ；

(2)、如图1，D点在数轴上表示的数为d ，则化简： $| d - a | - | d |$ ．（用含d的式子表示）

(3)、点M在数轴上表示的数为m ，点T表示的数为t；若数2是关于x的方程 $(a + 6) x - (a + b) x = \frac{1}{3} (x + 10) + 5 b^{2024} + 2 m$ 的解，且满足 $M T = 2 O M$ ，求t的值．

查看试题解析
25. 五年级下册我们学习了图形的旋转，你还记得吗？一起来动手完成下面的题目吧！
如图1，O为直线AB上一点，过点O作线段OC ，使得 $∠ A O C = 40 °$ ，将一直角（ $∠ M O N = 90 °$ ）放在点O处，一边ON在射线OA上，另一边OM与OC都在直线AB的上方．

(1)、将图1中的直角（ $∠ M O N = 90 °$ ）绕点O以每秒4°的速度沿逆时针方向旋转一周．如图2，经过t秒后，OM恰好平分 $∠ B O C$ ．则t的值为；

(2)、在（1）问的基础上，若直角（ $∠ M O N = 90 °$ ）在转动的同时，线段OC也绕O点以每秒7°的速度沿逆时针方向旋转一周，如图3，那么经过多长时间OC平分 $∠ M O N$ ？请说明理由；

(3)、如图4，在（2）问的基础上，经过多长时间OC平分 $∠ M O B$ ？请说明理由．

查看试题解析

爱	拼	才
		会	赢	！