贵州省铜仁市印江土家族苗族自治县2023-2024学年七年级上学期期末数学试题
试卷更新日期:2024-03-13 类型:期末考试
一、选择题(本大题共12个小题,每小题3分,共36分)本题每小题均有A、B、C、D四个备选答案,其中只有一个是正确的,请你将正确答案填涂在相应的答题卡上.
-
1. 中国人最早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史首次正式引入负数.如果收入50元,记作元,那么支出30元记作( )A、元 B、元 C、元 D、元2. 的倒数为( )A、 B、 C、2024 D、3. 下列各组单项式中,不是同类项的是( )A、与 B、与 C、与 D、与4. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4500000000人,将这个数用科学记数法表示为( )A、 B、 C、 D、5. 下列去括号错误的是( )A、 B、 C、 D、6. 下列各式: , , , , , , , 中,整式有( )A、7个 B、6个 C、4个 D、3个7. 若关于的方程是一元一次方程,则的值为( )A、 B、 C、2 D、8. 如果与互为补角,那么( )A、 B、 C、 D、9. 实数a , b在数轴上的位置如图所示,以下说法正确的是( )
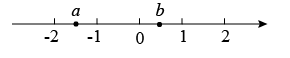 A、a+b=0 B、b<a C、ab>0 D、|b|<|a|10. 2022年10月22日,中国共产党第二十次全国代表大会在北京人民大会堂胜利闭幕,为了解我县初中生对“党的二十大”精神的知晓情况,从全县14700名初中生中随机抽取了1500名学生进行调查,在这次调查中,样本是( )A、1500 B、所抽取的1500名初中生对“党的二十大”精神的知晓情况 C、14700名初中生 D、每一名初中生对“党的二十大”精神的知晓情况11. 观察市统计局公布的五年期间某县农村居民人均收入每年比上一年增长率的统计图,下列说法正确的是( )
A、a+b=0 B、b<a C、ab>0 D、|b|<|a|10. 2022年10月22日,中国共产党第二十次全国代表大会在北京人民大会堂胜利闭幕,为了解我县初中生对“党的二十大”精神的知晓情况,从全县14700名初中生中随机抽取了1500名学生进行调查,在这次调查中,样本是( )A、1500 B、所抽取的1500名初中生对“党的二十大”精神的知晓情况 C、14700名初中生 D、每一名初中生对“党的二十大”精神的知晓情况11. 观察市统计局公布的五年期间某县农村居民人均收入每年比上一年增长率的统计图,下列说法正确的是( )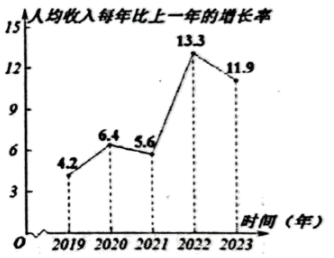 A、2021年农村居民人均收入低于2020年; B、农村居民人均收入比上年增长率低于的有2年; C、农村居民人均收入每年比上一年的增长率有大有小,但农村居民人均收入在持续增加; D、农村居民人均收入最多是2022年.12. 下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈, , 按此规律排列,则第⑨个图形中小圆圈的个数为( )
A、2021年农村居民人均收入低于2020年; B、农村居民人均收入比上年增长率低于的有2年; C、农村居民人均收入每年比上一年的增长率有大有小,但农村居民人均收入在持续增加; D、农村居民人均收入最多是2022年.12. 下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈, , 按此规律排列,则第⑨个图形中小圆圈的个数为( )
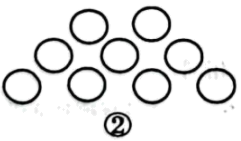
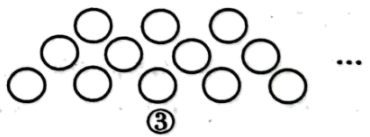 A、30 B、27 C、24 D、21
A、30 B、27 C、24 D、21二、填空题(本题共4个小题,每小题4分,共16分)
-
13. 单项式的系数是 , 次数是 .14. 若 , 则 .15. 规定一种运算“*” . 则方程的解为 .16. 如图.将面积为的小正方形与面积为的大正方形放在一起(>0,>0)则三角形ABC的面积是.

三、解答题(本大题共9个小题,第17,18,19,21,22题每题10分,第20,23,24,25题每题12分,共98分,要有解题的主要过程)
-
17. 计算:(1)、(2)、18. 解方程(1)、(2)、19. 某中学在开展课后延时服务过程性监测中,对七(9)班篮球兴趣小组的学生进行1分钟定点投篮测试,以投进9个球为标准,多于标准的个数记为正数,不足的个数记为负数,其中8名学生的成绩为: , , , , , , , .(1)、这8名学生中达到标准的占百分之几?(2)、他们共投进了多少个篮球?20. 学校为了调查学生对教学的满意度,随机抽取了部分学生作问卷调查:用“A”表示“很满意”,“B”表示“满意”,“C”表示“比较满意”,“D”表示“不满意”,如图甲、乙是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
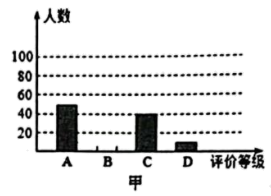
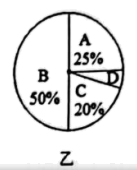 (1)、本次问卷调查,共调查了多少名学生?(2)、求出“B”部分表示“满意”学生的人数,并将图甲中“B”部分的图形补充完整;(3)、求出乙图中“D”部分表示“不满意”扇形的圆心角.21. 如图,线段 , 是线段上一点, , 是的中点,是的中点.
(1)、本次问卷调查,共调查了多少名学生?(2)、求出“B”部分表示“满意”学生的人数,并将图甲中“B”部分的图形补充完整;(3)、求出乙图中“D”部分表示“不满意”扇形的圆心角.21. 如图,线段 , 是线段上一点, , 是的中点,是的中点.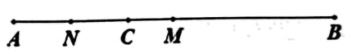 (1)、求线段的长;(2)、求线段的长.22. 下面是小明先化简再求值的全过程
(1)、求线段的长;(2)、求线段的长.22. 下面是小明先化简再求值的全过程, 其中 , .
解:
①
②
当时,原式 ③
④
⑤
(1)、请指出小明从第步开始出错;(2)、写出正确的化简求值过程.23. 助力脱贫攻坚成果,切实减轻农民负担,惠及普通百姓,中国某通讯公司,开设了两种普通通讯业务,分别是:①“本地通”用户先缴25元月租,然后每分钟通话费用0.2元;②“神州行”用户不用缴纳月租费,每分钟通话0.4元.(通话均指拨打本地电话)(1)、设一个月内通话时间约为分钟,这两种通讯方式用户每月需缴的费用是多少元?(用含的式子表示)(2)、一个月内通话多少分钟,两种通讯方式费用相同?(3)、若张阿姨一个月通话约90分钟,请你给她提个建议,应选择哪种通讯方式合算一些?请说明理由.24. 观联下列等式 , , ….将以上三个等式两边分别相加得:
.
(1)、猜想并写出: .(2)、直接写出下列各式的计算结果: .(3)、探究并计算: .25. 如图 1,点 O 为直线 AB 上一点,过点 O 作射线 OC,将一直角的直角顶点放在点 O 处,即∠MON,反向延长射线 ON,得到射线 OD.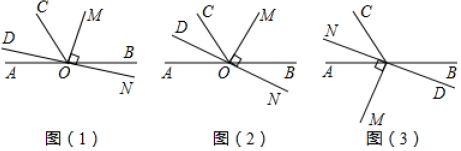 (1)、当∠MON 的位置如图(1)所示时,使∠NOB=20°,若∠BOC=120°,求∠COD 的度数.(2)、当∠MON 的位置如图(2)所示时,使一边 OM 在∠BOC 的内部,且恰好平分∠ BOC,问:射线 ON 的反向延长线 OD 是否平分∠AOC?请说明理由;注意:不能用问题(1)中的条件.(3)、当∠MON 的位置如图(3)所示时,射线 ON 在∠AOC 的内部,若∠BOC=120°.试探究∠AOM 与∠NOC 之间的数量关系,不需要说明理由,直接写出结论.
(1)、当∠MON 的位置如图(1)所示时,使∠NOB=20°,若∠BOC=120°,求∠COD 的度数.(2)、当∠MON 的位置如图(2)所示时,使一边 OM 在∠BOC 的内部,且恰好平分∠ BOC,问:射线 ON 的反向延长线 OD 是否平分∠AOC?请说明理由;注意:不能用问题(1)中的条件.(3)、当∠MON 的位置如图(3)所示时,射线 ON 在∠AOC 的内部,若∠BOC=120°.试探究∠AOM 与∠NOC 之间的数量关系,不需要说明理由,直接写出结论.