贵州省遵义市播州区2023-2024学年八年级上学期期末数学试卷
试卷更新日期:2024-03-13 类型:期末考试
一、选择题:本题共12小题,每小题4分,共48分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 下列四幅中国文字图案中,是轴对称图形的是( )A、
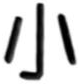 B、
B、 C、
C、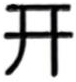 D、
D、 2. 某科学家研究发现人类头发的直径是分米将用科学记数法表示为( )A、 B、 C、 D、3. 若 , 则( )A、 B、 C、 D、4. 有两根和长的木棒,再找一根木棒与这两根木棒构成一个三角形木架可以选择的木棒是( )A、 B、 C、 D、5. 计算的结果为( )A、 B、 C、 D、6. 将分式方程去分母,两边同时乘后的式子为( )A、 B、 C、 D、7. 年月日,贵南高铁全线通车,其中有一隧道全线长如图,在隧道进口处的正西方处有一人,高铁从处沿北偏西的方向穿过隧道,在出口处鸣笛,出口处在处的正北方,已知声音在空气中的传播速度为 , 经过多少秒进口处的人能够听到鸣笛声?不考虑其他因素( )
2. 某科学家研究发现人类头发的直径是分米将用科学记数法表示为( )A、 B、 C、 D、3. 若 , 则( )A、 B、 C、 D、4. 有两根和长的木棒,再找一根木棒与这两根木棒构成一个三角形木架可以选择的木棒是( )A、 B、 C、 D、5. 计算的结果为( )A、 B、 C、 D、6. 将分式方程去分母,两边同时乘后的式子为( )A、 B、 C、 D、7. 年月日,贵南高铁全线通车,其中有一隧道全线长如图,在隧道进口处的正西方处有一人,高铁从处沿北偏西的方向穿过隧道,在出口处鸣笛,出口处在处的正北方,已知声音在空气中的传播速度为 , 经过多少秒进口处的人能够听到鸣笛声?不考虑其他因素( ) A、 B、 C、 D、8. 数学活动课上,小星制作了一个燕尾形的风筝如图, , , 他准备用刻度尺量和的长是否相等.
A、 B、 C、 D、8. 数学活动课上,小星制作了一个燕尾形的风筝如图, , , 他准备用刻度尺量和的长是否相等.
小英却说:“不用再测量,因为≌ , 所以”
小英用到的判定三角形全等的方法是( )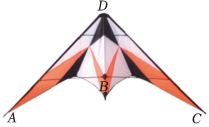 A、 B、 C、 D、9. 某中学举行攀登一座高的山,第一小组的攀登速度是第二小组的倍第一小组比第二小组早到达山顶,求两个小组的攀登速度各是多少,若设第二小组的速度为 , 则可列出方程为( )A、 B、 C、 D、10. 如图,在中,是高,平分 , , , 则的度数是( )
A、 B、 C、 D、9. 某中学举行攀登一座高的山,第一小组的攀登速度是第二小组的倍第一小组比第二小组早到达山顶,求两个小组的攀登速度各是多少,若设第二小组的速度为 , 则可列出方程为( )A、 B、 C、 D、10. 如图,在中,是高,平分 , , , 则的度数是( ) A、 B、 C、 D、11. 如图,、、 , 是六边形的四个外角,延长交于点若 , 则的度数为( )
A、 B、 C、 D、11. 如图,、、 , 是六边形的四个外角,延长交于点若 , 则的度数为( ) A、 B、 C、 D、12. 已知实数满足 , 则的值为( )A、 B、 C、 D、
A、 B、 C、 D、12. 已知实数满足 , 则的值为( )A、 B、 C、 D、二、填空题:本题共4小题,每小题4分,共16分。
-
13. 分解因式: =.
14. 如图,在中, , 边的垂直平分线交于点 , 交于点且 , , 则的长是 . 15. 如图,在中, , 以点为圆心、的长为半径画弧,交于点、分别以点、为圆心,大于的长为半径画弧,两弧交于点 , 作射线交于点若 , 则的值为 .
15. 如图,在中, , 以点为圆心、的长为半径画弧,交于点、分别以点、为圆心,大于的长为半径画弧,两弧交于点 , 作射线交于点若 , 则的值为 .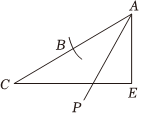 16. 如图,中, , , 是线段上一动点,以为边在下方作等边三角形若 , , 则的最小值为 .
16. 如图,中, , , 是线段上一动点,以为边在下方作等边三角形若 , , 则的最小值为 .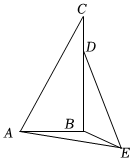
三、解答题:本题共8小题,共86分。解答应写出文字说明,证明过程或演算步骤。
-
17.
(1)、计算:;(2)、解方程: .18. 先化简,再求值: , 其中 .19. 如图,已知点 , , 、在同一条直线上, , , . (1)、求证:≌;(2)、若 , 求的度数.20. 如图,在平面直角坐标系中,已知点 , , , 连接 , , , 得到 .
(1)、求证:≌;(2)、若 , 求的度数.20. 如图,在平面直角坐标系中,已知点 , , , 连接 , , , 得到 .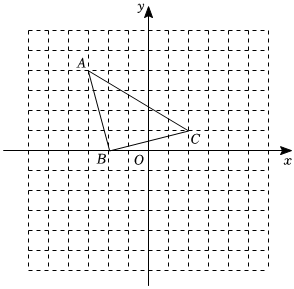 (1)、将向右平移两个单位长度得到 , 则 , , ;(2)、在的情况下,画出关于轴对称的图形;(3)、连接 , 得到 , 求出的面积.21. 某水果店从种植园花费元购进种草莓,元购进种草莓,已知种草莓的进价是种草莓进价的倍,种草莓的数量比种草莓的数量多千克.(1)、求种草莓每千克的进价;(2)、若该水果店计划两周内销售完这批草莓,第一周:以元千克的价格售出种草莓千克,以元千克的价格售出种草莓千克;第二周:把剩下的 , 两种草莓每千克的利润减少一半后出售,若该水果店售完这些草莓的获利不低于元,求的最小值.22. 如图,在四边形中,于点 , , 且平分 , 平分 .
(1)、将向右平移两个单位长度得到 , 则 , , ;(2)、在的情况下,画出关于轴对称的图形;(3)、连接 , 得到 , 求出的面积.21. 某水果店从种植园花费元购进种草莓,元购进种草莓,已知种草莓的进价是种草莓进价的倍,种草莓的数量比种草莓的数量多千克.(1)、求种草莓每千克的进价;(2)、若该水果店计划两周内销售完这批草莓,第一周:以元千克的价格售出种草莓千克,以元千克的价格售出种草莓千克;第二周:把剩下的 , 两种草莓每千克的利润减少一半后出售,若该水果店售完这些草莓的获利不低于元,求的最小值.22. 如图,在四边形中,于点 , , 且平分 , 平分 .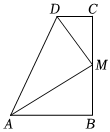 (1)、求证:为的中点;(2)、若 , , 求四边形的面积.23. 【提出问题】某数学活动小组对多项式乘法进行如下探究:
(1)、求证:为的中点;(2)、若 , , 求四边形的面积.23. 【提出问题】某数学活动小组对多项式乘法进行如下探究:
;
;
.
通过以上计算发现,形如的两个多项式相乘,其结果一定为为整数
因为因式分解是与整式乘法是方向相反的变形,所以一定有 , 即可将形如的多项式因式分解成、为整数 .
例如: .(1)、【初步应用】用上面的方法分解因式: ;(2)、【类比应用】规律应用:若可用以上方法进行因式分解,则整数的所有可能值是;(3)、【拓展应用】分解因式: .24. 【提出问题】如图 , 在等腰中, , 分别以 , 为边作等边和等边 , 与相交于点 , 连接 .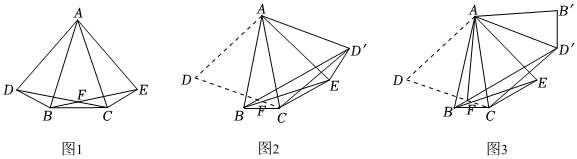 (1)、【初步探究】如图 , 连接 , 求证:≌ .(2)、【深入探究】如图 , 将沿翻折得到 , 连接 , , 类比的探究方法发现:
(1)、【初步探究】如图 , 连接 , 求证:≌ .(2)、【深入探究】如图 , 将沿翻折得到 , 连接 , , 类比的探究方法发现:
结论:_▲_≌;
结论: .
请证明结论 .(3)、如图、在的情况下将线段沿翻折得到线段 , 连接 , , 试判断线段与的位置关系.