备战2024年中考数学细点逐一突破真题训练第13章图形的相似

试卷更新日期：2024-03-13 类型：一轮复习

进入出卷网下载

一、相似型

1. 下列各组图形不是相似图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图所示的两个四边形相似，则下列结论不正确的是（）

A、 $a = 2 \sqrt{2}$ B、 $m = 2 n$ C、 $x = 2$ D、 $∠ α = 60 °$

查看试题解析
3. 将一张 $▱ A B C D$ （ $A D < A B < 2 A D$ ）纸片，以它的一边为边长剪去一个菱形，将余下的平行四边形中，再以它的一边为边长剪去一个菱形，若剪去两个菱形后所剩下的平行四边形与原来 $▱ A B C D$ 相似，则 $▱ A B C D$ 的相邻两边 $A D$ 与 $A B$ 的比值是（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{5} - 1}{2}$ C、 $\frac{\sqrt{2}}{2}$ 或 $\frac{\sqrt{5} - 1}{2}$ D、 $\sqrt{2} - 1$ 或 $\frac{\sqrt{2}}{2}$ 或 $\frac{\sqrt{5} - 1}{2}$

查看试题解析
4. 如图，矩形ABCD中，AB＝2，BC＝4，剪去一个矩形ABEF后，余下的矩形EFDC∽矩形BCDA，则EC的长为.

查看试题解析

二、平行线平分线段成比例

5. 如图，已知 $A B / / C D / / E F ， A D = 3 ， B C = 4 ， D F = 5$ ，则 CE的长为（）

A、 $\frac{32}{3}$ B、 $\frac{20}{3}$ C、6 D、 $\frac{15}{4}$

查看试题解析
6. 如图，在 $△ A B C$ 中， $D E / / B C$ 分别交AC，AB于点 $D ， E ， E F / / A C$ 交BC于点 $F ， \frac{A E}{B E} = \frac{2}{5} ， B F = 8$ ，则DE的长为（）

A、 $\frac{16}{5}$ B、 $\frac{16}{7}$ C、2 D、3

查看试题解析
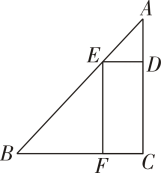7. 如图，在 $△ A B C$ 中，点D在BC边上，连接AD ，点C在线段AD上， $G E ∥ B D$ ，且交AD于点E ， $G F ∥ A C$ ，且交CD于点F ，则下列结论一定正确的是（）

A、 $\frac{A B}{A E} = \frac{A G}{A D}$ B、 $\frac{D F}{C F} = \frac{D G}{A D}$ C、 $\frac{A E}{B E} = \frac{C F}{D F}$ D、 $\frac{F G}{A C} = \frac{E G}{B D}$

查看试题解析
8. 【教材呈现】华师版九年级上册63页例1．
如图，在△ABC中，点D是边AB的三等分点，DE∥BC，DE=5，求BC的长．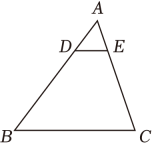

【应用拓展】

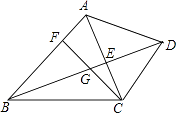
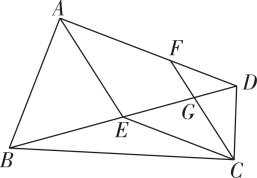
(1)、如图①，在△ABC中，点D是边AB的中点，点F为BC延长线上一点，连接DF交AC于点E，若DE：EF=3：1，DG∥AC，EC=2，则AC的长为．

(2)、如图②，在△ABC中，点D为边BA延长线上一点，点E为BC上一点，连接DE交AC于点F，若点A为DB的中点，CE：EB=1：2，△DBE的面积为4，则△CFE（阴影部分）面积为．

查看试题解析
9. 阅读与计算，请阅读以下材料，完成相应的任务．
材料：三角形的内角平分线定理：
如图1，在 $Δ A B C$ 中， $A D$ 平分 $∠ B A C$ ，交 $B C$ 于点 $D$ ，则 $\frac{A B}{A C} = \frac{B D}{C D}$ ．
下面是这个定理的部分证明过程．
证明：如图2，过 $C$ 作 $C E ∥ D A$ ，交 $B A$ 的延长线于点 $E$ ．

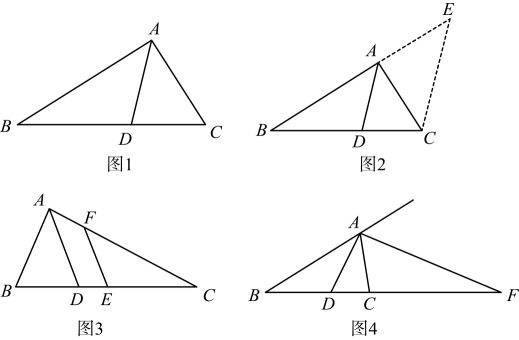(1)、【思路说明】请按照上面的证明思路，写出该证明的剩余部分；

(2)、【直接应用】如图3， $△ A B C$ 中， $E$ 是 $B C$ 中点， $A D$ 是 $∠ B A C$ 的平分线， $E F ∥ A D$ 交 $A C$ 于 $F$ ．若 $A B = 11$ ， $A C = 15$ ，求线段 $F C$ 的长；

(3)、【拓展延伸】如图4， $△ A B C$ 中， $A D$ 平分 $∠ B A C$ ， $B C$ 的延长线交 $△ A B C$ 外角角平分线 $A F$ 于点 $F$ ．
①找出 $A B$ 、 $A C$ 、 $B F$ 、 $C F$ 这四条线段的比例关系，并证明；
②若 $B D = 2$ ， $C F = 4$ ，求 $C D$ 的长．

查看试题解析

三、相似三角形判定

10. 如图，已知 $∠ 1 = ∠ 2$ ，那么添加下列一个条件后，不能判定 $△ A B C ∽ △ A D E$ 的是（）

A、 $∠ C = ∠ E$ B、 $∠ B = ∠ A D E$ C、 $\frac{A B}{A D} = \frac{A C}{A E}$ D、 $\frac{A B}{A D} = \frac{B C}{D E}$

查看试题解析
11. 如图，△ABC中，∠A=70°，AB=4，AC= 6，将△ABC沿图中的虚线剪开，则剪下的阴影三角形与原三角形不相似的是（）

A、 B、 C、 D、

查看试题解析
12. 如图，点E在正方形ABCD的对角线AC上，EF⊥AB于点F，连结DE并延长，交边BC于点M，交边AB的延长线于点G.若AF=2，FB=1，则MG=（）

A、 $2 \sqrt{3}$ B、 $\frac{3 \sqrt{5}}{2}$ C、 $\sqrt{5} + 1$ D、 $\sqrt{10}$

查看试题解析
13. 如图，点 $D$ 在等边 $△ A B C$ 的 $B C$ 边上， $△ A D E$ 为等边三角形， $D E$ 与 $A C$ 交于点 $F$ ．求证： $△ A B D ∽ △ D C F$ ．

查看试题解析
14. $D$ 、 $E$ 分别是 $△ A B C$ 的边 $A B$ ， $A C$ 上的点，如果 $∠ A = 45 °$ ， $A B = 2$ ， $A D = 1$ ， $A C = 3$ ，那么要使 $△ A B C$ 和 $△ A D E$ 相似，则 $A E =$ ．

查看试题解析

四、相似三角形实际应用

15. 据 $《$ 墨经 $》$ 记载，在两千多年前，我国学者墨子和他的学生做了“小孔成像”实验，阐释了光的直线传播原理 $.$ 小孔成像的示意图如图所示，光线经过小孔 $O$ ，物体 $A B$ 在幕布上形成倒立的实像 $C D ($ 点 $A$ 、 $B$ 的对应点分别是 $C$ 、 $D) .$ 若物体 $A B$ 的高为 $5 c m$ ，小孔 $O$ 到地面距离 $O E$ 为 $2 c m$ ，则实像 $C D$ 的高度为（）

A、 $\frac{10}{3} c m$ B、 $\frac{14}{5} c m$ C、 $\frac{4}{3} c m$ D、 $\frac{3}{10} c m$

查看试题解析
16. 如图， $E B$ 为驾驶员的盲区，驾驶员的眼睛点 $P$ 处与地面 $B E$ 的距离为 $1.6$ 米，车头 $F A C D$ 近似看成一个矩形，且满足 $3 F D = 2 F A$ ，若盲区 $E B$ 的长度是 $6$ 米，则车宽 $F A$ 的长度为（）米.

A、 $1.8$ B、 $2$ C、 $\frac{11}{7}$ D、 $\frac{12}{7}$

查看试题解析
17. 学习了相似三角形知识后，小丽同学准备用自制的直角三角形纸板测量校园内一颗古树的高度．已知三角形纸板的斜边长为0.5米，较短的直角边长为0.3米．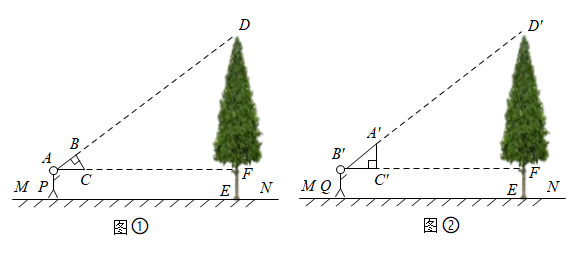

(1)、小丽先调整自己的位置至点 $P$ ，将直角三角形纸板的三个顶点位置记为 $A$ 、 $B$ 、 $C$ （如图①），斜边 $A B$ 平行于地面 $M N$ （点 $M$ 、 $P$ 、 $E$ 、 $N$ 在一直线上），且点 $D$ 在边 $A C$ （较长直角边）的延长线上，此时测得边 $A B$ 距离地面的高度 $E F$ 为1.5米，小丽与古树的距离 $A F$ 为16米，求古树的高度 $D E$ ；

(2)、为了尝试不同的思路，小丽又向前移动自己的位置至点 $Q$ ，将直角三角形纸板的三个顶点的新位置记为 $A^{'}$ 、 $B^{'}$ 、 $C^{'}$ （如图②），使直角边 $B^{^{'}} C^{^{'}}$ （较短直角边）平行于地面 $M N$ （点 $M$ 、 $Q$ 、 $E$ 、 $N$ 在一直线上），点 $D$ 在斜边 $B^{'} A^{'}$ 的延长线上，且测得此时边 $B^{^{'}} C^{^{'}}$ 距离地面的高度依然是1.5米，那么小丽向前移动了多少米？

查看试题解析
18. 小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关 $.$ 因此，他们认为：可以借助物体的影子长度计算光源到物体的位置 $.$ 于是，他们做了以下尝试．

(1)、如图 $1$ ，垂直于地面放置的正方形框架 $A B C D$ ，边长 $A B$ 为 $30 c m$ ，在其上方点 $P$ 处有一灯泡，在灯泡的照射下，正方形框架的横向影子 $A' B$ ， $D' C$ 的长度和为 $6 c m .$ 那么灯泡离地面的高度 $P M$ 为多少．

(2)、不改变图 $1$ 中灯泡的高度，将两个边长为 $30 c m$ 的正方形框架按图 $2$ 摆放，请计算此时横向影子 $A' B$ ， $D' C$ 的长度和为多少？

查看试题解析
19. 如图，在正方形网格中，点 $A$ 、 $B$ 、 $C$ 都在格点上，利用格点按要求完成下列作图．（要求仅用无刻度的直尺，不要求写画法，保留必要的作图痕迹）

(1)、在图（1）中，以 $C$ 为位似中心，位似比为1：2，在格点上将 $Δ A B C$ 放大得到 $Δ A_{1} B_{1} C_{1}$ ；请画出 $Δ A_{1} B_{1} C_{1}$

(2)、在图（3）中，线段 $A B$ 上作点 $M$ ，利用格点作图使得 $\frac{A M}{B M} = \frac{2}{3}$

(3)、在图（2）中，利用格点在 $A C$ 边上作一个点 $D$ ，使得 $△ A B D ∽ △ A C B$ ．

查看试题解析
20. 阅读下列材料，解决问题：
配方法是数学中一种很重要的恒等变形方法，我们已经学习了用配方法解一元二次方程，并在此基础上得出了一元二次方程的求根公式．其实配方法还有很多重要的应用．例如我们可以用配方法求代数式的最值及取得最值的条件，如下面的例子：
例：求多项式 $2 x^{2} - 8 x + 1$ 的最小值
解： $2 x^{2} - 8 x + 1 = 2 (x^{2} - 4 x) + 1$
$\begin{array}{l} = 2 (x^{2} - 4 x + 4 - 4) + 1 \end{array}$
$= 2 (x - 2)^{2} - 7$
$\begin{array}{l} ∵ (x - 2)^{2} \geq 0 \end{array}$ ，
$∴ 2 (x - 2)^{2} - 7 \geq - 7$
$∴$ 多项式的最小值为−7，此时， $x = 2$ ．
仿照上面的方法，解决下面的问题：

(1)、当 $x =$ 时，多项式 $- x^{2} - 4 x + 3$ 有最值是；

(2)、若代数式 $M = 2 x^{2} - 3 y^{2} - x - 1 ， N = x^{2} - 3 y^{2} + x - 4$ ，试比较 $M$ 与 $N$ 的大小关系；

(3)、如图，在 $△ A B C$ 中， $B C = a$ ，高 $A D = b$ ，矩形 $E F G H$ 的四个顶点分别在三角形的三边上，设 $H E = x$ ，矩形 $E F G H$ 的面积为 $S$ ．用含有 $x ， a ， b$ 的代数式表示 $S$ ，并求出当 $x$ 的值为多少时， $S$ 的值最大？并判断此时 $S$ 与 $△ A B C$ 面积的关系．

查看试题解析

五、相似三角形的相关证明计算

21. 如图，点E在矩形ABCD的BC边上，将 $△ A E B$ 沿AE翻折得到△AEF，过点F作 $P Q ∥ A B$ ，交BC、AD于点P、Q．

(1)、求证： $△ P E F ∽ △ Q F A$ ．

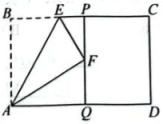(2)、已知 $A B = \sqrt{3}$ ，若△AEF与△AFQ相似，直接写出BE的长．

查看试题解析
22. 已知：如图，在四边形ABCD中，AB∥CD，对角线AC、BD交于点E，点F在边AB上，连接CF交线段BE于点G，CG²=GE•GD．

(1)、求证：∠ACF=∠ABD；

(2)、连接EF，求证：EF•CG=EG•CB．

查看试题解析
23. 如图，矩形 $A B C D$ 中， $B C < 2 A B$ ，点M是 $B C$ 的中点，连接 $A M$ ．将 $△ A B M$ 沿着 $A M$ 折叠后得 $△ A P M$ ，延长 $A P$ 交 $C D$ 于E ，连接 $M E$ ．

(1)、求证： $M E$ 平分 $∠ P M C$ ；

(2)、求证：△EMC∽△MAB.

查看试题解析
24. 已知：如图，四边形ABCD中， $∠ B A D = ∠ B C D$ $= 9 0^{°} ， E$ 为对角线BD的中点，点 $F$ 在边AD上，CF交BD于点 $G ， C F / / A E ， C F = \frac{1}{2} B D$ .

(1)、求证：四边形AECF为菱形；

(2)、 $∠ D C G = ∠ D E C$ ，求证： $A E^{2} = A D \cdot D C$ .

查看试题解析