备战2024年中考数学细点逐一突破真题训练第11章三角形
试卷更新日期:2024-03-13 类型:一轮复习
一、三角形三边关系
-
1. 下列说法错误的是( )A、三角形的三条中线交于一点 B、三角形任意两外角平分线所在直线的交点到三边的距离相等 C、三角形具有稳定性 D、形状相同的两个三角形全等2. 以下列各组长度的线段为边,能构成三角形的是( )A、8,4,3 B、6,8.15 C、4,6,5 D、7,5,123. 如图,在中,AD是边BC上的中线,若 , , 则AD的取值范围是( )
 A、无法确定 B、 C、 D、4. 已知等腰三角形的周长为19,其中一边长为3,则该等腰三角形的底边是( )A、3 B、8 C、3或8 D、135. 八(2)班数学兴趣小组在一次活动中进行了探究实验活动,请你和他们一起活动吧.
A、无法确定 B、 C、 D、4. 已知等腰三角形的周长为19,其中一边长为3,则该等腰三角形的底边是( )A、3 B、8 C、3或8 D、135. 八(2)班数学兴趣小组在一次活动中进行了探究实验活动,请你和他们一起活动吧.
[发现问题]他们在探究实验活动中遇到了下面的问题:如图1,是的中线,若 , 求的取值范围.
[探究方法]他们通过探究发现,延长至点E , 使 , 连接 . 可以证出 , 利用全等三角形的性质可将已知的边长与转化到中,进而求出的取值范围.
方法小结:从上面的思路可以看出,解决问题的关键是将中线延长一倍,构造出全等三角形,我们把这种方法叫做“倍长中线法”.
[问题解决]
(1)、请你利用上面解答问题的思路方法,写出求的取值范围的过程.(2)、如图2,是的中线,且 , 求证: .二、三角形有关的重要线段
-
6. 如图,四个图形中,线段是的高的图是( )A、
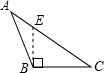 B、
B、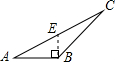 C、
C、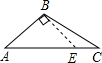 D、
D、 7. 如图, , , 分别是的高、角平分线、中线,则下列结论错误的是( )
7. 如图, , , 分别是的高、角平分线、中线,则下列结论错误的是( ) A、 B、 C、 D、8. 如图,下面是三位同学的折纸示意图,则依次是的( )
A、 B、 C、 D、8. 如图,下面是三位同学的折纸示意图,则依次是的( ) A、中线、角平分线、高线 B、高线、中线、角平分线 C、角平分线、高线、中线 D、角平分线、中线、高线9. 如图,D是BC的中点,E是AD的中点,F是CE的中点,三角形ABC的面积为16,则三角形DEF的面积为;
A、中线、角平分线、高线 B、高线、中线、角平分线 C、角平分线、高线、中线 D、角平分线、中线、高线9. 如图,D是BC的中点,E是AD的中点,F是CE的中点,三角形ABC的面积为16,则三角形DEF的面积为;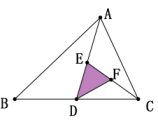 10. 如图所示,AE是的内角平分线,AF是的高, , , 求.
10. 如图所示,AE是的内角平分线,AF是的高, , , 求.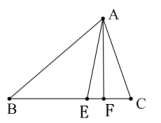 11. 为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小丽在组内做了如下尝试:如图1,在中,是边上的中线,延长到 , 使 , 连接 .
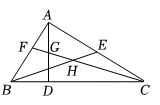
11. 为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小丽在组内做了如下尝试:如图1,在中,是边上的中线,延长到 , 使 , 连接 .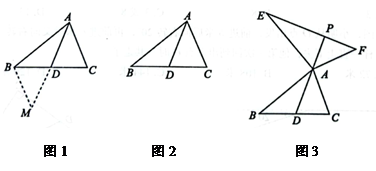 (1)、【探究发现】图1中与的数量关系是 , 位置关系是;(2)、【初步应用】如图2,在中,若 , 求边上的中线的取值范围;(3)、【探究提升】如图3,是的中线,过点分别向外作 , 使得 , 延长交于点 , 判断线段与的数量关系和位置关系,请说明理由.12. 如图,在中, , , 是边上的高,是边的中线,是的角平分线,交于点 , 交于点.
(1)、【探究发现】图1中与的数量关系是 , 位置关系是;(2)、【初步应用】如图2,在中,若 , 求边上的中线的取值范围;(3)、【探究提升】如图3,是的中线,过点分别向外作 , 使得 , 延长交于点 , 判断线段与的数量关系和位置关系,请说明理由.12. 如图,在中, , , 是边上的高,是边的中线,是的角平分线,交于点 , 交于点.①;②;③;④.
其中一定正确的是.(写出所有正确结论的序号)
三、等腰三角形有关证明及计算
-
13. 已知等腰三角形一个内角是 , 则它的底角的度数为( )A、 B、 C、 D、或14. 将一根橡皮筋两端固定在点A , B处,拉展成线段AB , 拉动橡皮筋上的一点P , 当△APB是顶角为120°的等腰三角形时,已知AB=6cm , 则橡皮筋被拉长了( )
 A、2cm B、4cm C、 D、15. 如图, , 为方格纸中格点上的两点,若以为边,在方格中取一点(在格点上),使得为等腰三角形,则点的个数为( )
A、2cm B、4cm C、 D、15. 如图, , 为方格纸中格点上的两点,若以为边,在方格中取一点(在格点上),使得为等腰三角形,则点的个数为( )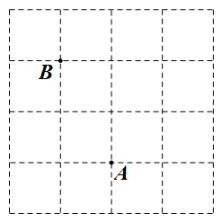 A、 B、 C、 D、16. 在中, , 分别过点B , C作平分线的垂线,垂足分别为点D , E , BC的中点是M , 连接CD , MD , ME . 则下列结论错误的是( )A、 B、 C、 D、
A、 B、 C、 D、16. 在中, , 分别过点B , C作平分线的垂线,垂足分别为点D , E , BC的中点是M , 连接CD , MD , ME . 则下列结论错误的是( )A、 B、 C、 D、四、三角形的四心(内心、外心、重心、旁心)
-
17. 如图,在已知的△ABC中,按以下步骤:(1)分别以B、C为圆心,大于BC的长为半径作弧,两弧相交M、N;(2)作直线MN,交AB于D,连接CD,若CD=AD,∠B=25°,则下列结论中错误的是( )
 A、直线MN是线段BC的垂直平分线 B、点D为△ABC的外心 C、∠ACB=90° D、点D为△ABC的内心18. 如图,在正方形网格中,△ABC的顶点在格点(网格线的交点)上,请仅用无刻度直尺完成以下作图.(保留作图痕迹)
A、直线MN是线段BC的垂直平分线 B、点D为△ABC的外心 C、∠ACB=90° D、点D为△ABC的内心18. 如图,在正方形网格中,△ABC的顶点在格点(网格线的交点)上,请仅用无刻度直尺完成以下作图.(保留作图痕迹)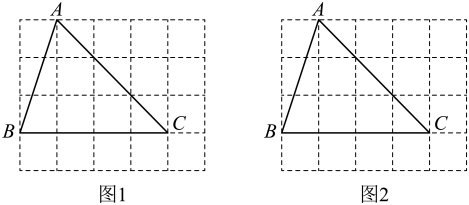 (1)、在图1中作△ABC的重心.(2)、在图2中作 , 且G是格点.19. 如图,是的内切圆, , 过点I作分别交 , 于N,M,若 , , 则的半径是( )
(1)、在图1中作△ABC的重心.(2)、在图2中作 , 且G是格点.19. 如图,是的内切圆, , 过点I作分别交 , 于N,M,若 , , 则的半径是( )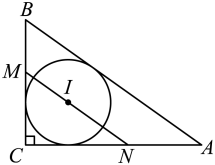 A、 B、 C、 D、
A、 B、 C、 D、五、三角形内角和及内外角关系
-
20. 如图, , , 则的度数为( )
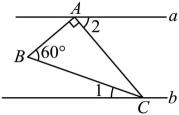 A、 B、 C、 D、21. 如图, , , , , 则的度数等于( )
A、 B、 C、 D、21. 如图, , , , , 则的度数等于( ) A、 B、 C、 D、22. 如图,将三角形纸片沿折叠,当点A落在四边形的外部时,测量得 , , 则为( )
A、 B、 C、 D、22. 如图,将三角形纸片沿折叠,当点A落在四边形的外部时,测量得 , , 则为( )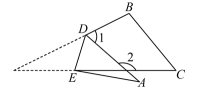 A、 B、 C、 D、23. 如图,把三角形纸片ABC沿DE折叠,当点A落在四边形BCDE外部时,则∠A与∠1、∠2之间的数量关系是( )
A、 B、 C、 D、23. 如图,把三角形纸片ABC沿DE折叠,当点A落在四边形BCDE外部时,则∠A与∠1、∠2之间的数量关系是( )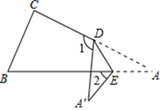 A、 B、 C、 D、24. 如图,把沿对折,叠后的图形如图所示.若 , , 则的度数为( )
A、 B、 C、 D、24. 如图,把沿对折,叠后的图形如图所示.若 , , 则的度数为( ) A、24° B、25° C、30° D、35°
A、24° B、25° C、30° D、35°六、直角三角形有关证明及计算
-
25. 下列三角形中,不是直角三角形的是( )A、中, B、中, , C、中, D、中,三边之比为26. △ABC三边长为a、b、c , 则下列条件能判断△ABC是直角三角形的是( )A、 B、 C、a=12,b=5,c=13 D、27. 如图,已知 , , , , 则°.
 28. 如图,CD为Rt△ABC斜边AB上的中线,E为AC的中点.若 , , 则DE= .
28. 如图,CD为Rt△ABC斜边AB上的中线,E为AC的中点.若 , , 则DE= . 29. 如图,在平面直角坐标系中已知点和点 , 是的中点,若有一动点在折线上运动,直线截所得的三角形为直角三角形,则点的坐标为 .
29. 如图,在平面直角坐标系中已知点和点 , 是的中点,若有一动点在折线上运动,直线截所得的三角形为直角三角形,则点的坐标为 .
七、三角形尺规作图题
-
30. 如图,在的正方形网格中,每个小正方形的顶点叫做格点,经过格点 , 仅用无刻度的直尺在给定网格中画图.(保留作图痕迹)
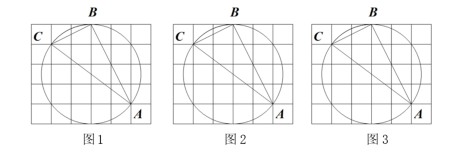 (1)、在图1中,画出的中线.(2)、在图2中,标出圆心 , 并画出的角平分线.(3)、在图3中,画出的边上的高线.31. 图、图、图均是的正方形网格,每个小正方形的边长均为 , 点 , , , 均在格点上,用无刻度的直尺在给定的网格中按要求画图:
(1)、在图1中,画出的中线.(2)、在图2中,标出圆心 , 并画出的角平分线.(3)、在图3中,画出的边上的高线.31. 图、图、图均是的正方形网格,每个小正方形的边长均为 , 点 , , , 均在格点上,用无刻度的直尺在给定的网格中按要求画图: (1)、如图 , 在上画一点 , 连结 , 使;
(1)、如图 , 在上画一点 , 连结 , 使;
(2)、如图 , 在上画一点 , 连结 , 使;
(3)、如图 , 在上画一点 , 连结 , , 使 .32. 如图①、图②均是的正方形网格,每个小正方形的边长均为1,的顶点均在格点上,用无刻度的直尺在给定的网格中按要求画图. (1)、在图①中的线段BC上找一点E , 连接AE , 使为等腰三角形.(2)、在图②中的线段AD上找一点F , 连接BF , 使为直角三角形.33. 图①、图②、图③均为4×4的正方形网格,每个小正方形的边长均为1,每个小正方形顶点称为格点,按下列要求作图:
(1)、在图①中的线段BC上找一点E , 连接AE , 使为等腰三角形.(2)、在图②中的线段AD上找一点F , 连接BF , 使为直角三角形.33. 图①、图②、图③均为4×4的正方形网格,每个小正方形的边长均为1,每个小正方形顶点称为格点,按下列要求作图: (1)、在图①中,作线段MN= , 点M、N均在格点上;(2)、在图②中,作正方形ABCD,使其面积为10,点A、B、C、D均在格点上;(3)、在图③中,作等腰直角三角形EFG,使其面积为 , 点E、F、G均在格点上.
(1)、在图①中,作线段MN= , 点M、N均在格点上;(2)、在图②中,作正方形ABCD,使其面积为10,点A、B、C、D均在格点上;(3)、在图③中,作等腰直角三角形EFG,使其面积为 , 点E、F、G均在格点上.