华师大版数学八年级下册第十七章 函数及其图像 单元测试
试卷更新日期:2024-03-13 类型:单元试卷
一、选择题(每题4分,共48分)
-
1. 下列各曲线中,能表示是的函数的是( )A、
 B、
B、 C、
C、 D、
D、 2. 中国象棋文化历史久远,雅俗共赏,具有广泛的参与度.象棋残局是象棋的基础,《七星聚会》素有“残局之王”的称谓,深受广大棋迷喜爱.如图就是残局《七星聚会》.如果建立平面直角坐标系,使“帥”位于点 , “象”位于点 , 那么“兵”在同一坐标系下的坐标是( )
2. 中国象棋文化历史久远,雅俗共赏,具有广泛的参与度.象棋残局是象棋的基础,《七星聚会》素有“残局之王”的称谓,深受广大棋迷喜爱.如图就是残局《七星聚会》.如果建立平面直角坐标系,使“帥”位于点 , “象”位于点 , 那么“兵”在同一坐标系下的坐标是( )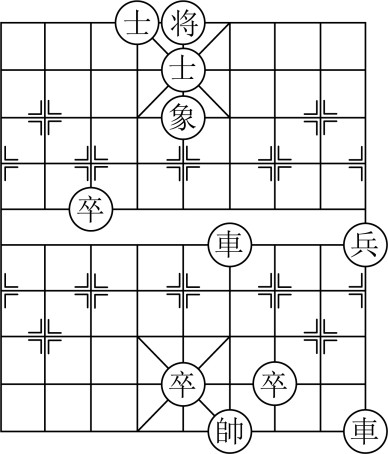 A、 B、 C、 D、3. 爷爷饭后出去散步,从家里出发20分钟后到一个离家900米的街心花园,与朋友聊天10分钟后,用15分钟返回家里.下面图形中表示爷爷离家的距离y(米)与离家时间x(分)之间函数关系的是( )A、
A、 B、 C、 D、3. 爷爷饭后出去散步,从家里出发20分钟后到一个离家900米的街心花园,与朋友聊天10分钟后,用15分钟返回家里.下面图形中表示爷爷离家的距离y(米)与离家时间x(分)之间函数关系的是( )A、 B、
B、 C、
C、 D、
D、 4. 小明用相同的积木玩一个拼图游戏,该积木每个角都是直角,长度如图1所示,小明用个这样的积木,按照如图2所示的方法玩拼图游戏,两两相扣,相互间不留空隙.则图形的总长度与图形个数之间的关系式为( )
4. 小明用相同的积木玩一个拼图游戏,该积木每个角都是直角,长度如图1所示,小明用个这样的积木,按照如图2所示的方法玩拼图游戏,两两相扣,相互间不留空隙.则图形的总长度与图形个数之间的关系式为( )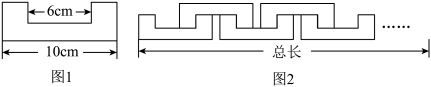 A、 B、 C、 D、5. 将一次函数的图像向右平移5个单位后,所得的直线与两坐标轴围成的三角形的面积是( )A、4 B、6 C、9 D、496. 已知是一次函数图象上的不同的两个点,若 , 则k的取值范围是( )A、 B、 C、 D、7. 点在正比例函数的图象上,则的值为( )A、 B、 C、 D、8. 已知函数 是反比例函数,则 的值为( )A、2 B、-2 C、2或-2 D、任意实数9. 在平面直角坐标系中,将直线沿轴向下平移2个单位后恰好经过原点,则的值为( )A、 B、2 C、4 D、10. 已知在平面直角坐标系中的位置如图所示,将各顶点横坐标不变,纵坐标都乘以后,得到 , 则点的坐标为( )
A、 B、 C、 D、5. 将一次函数的图像向右平移5个单位后,所得的直线与两坐标轴围成的三角形的面积是( )A、4 B、6 C、9 D、496. 已知是一次函数图象上的不同的两个点,若 , 则k的取值范围是( )A、 B、 C、 D、7. 点在正比例函数的图象上,则的值为( )A、 B、 C、 D、8. 已知函数 是反比例函数,则 的值为( )A、2 B、-2 C、2或-2 D、任意实数9. 在平面直角坐标系中,将直线沿轴向下平移2个单位后恰好经过原点,则的值为( )A、 B、2 C、4 D、10. 已知在平面直角坐标系中的位置如图所示,将各顶点横坐标不变,纵坐标都乘以后,得到 , 则点的坐标为( )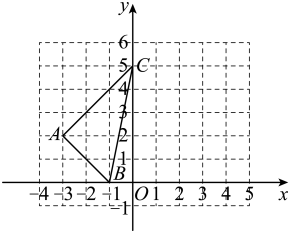 A、 B、 C、 D、11. 如图,点 落在第二象限内双曲线 上,过 两点分别作 轴的垂线段,垂足为 ,连接 ,若 且 ,则 的值为( )
A、 B、 C、 D、11. 如图,点 落在第二象限内双曲线 上,过 两点分别作 轴的垂线段,垂足为 ,连接 ,若 且 ,则 的值为( ) A、4 B、-4 C、2 D、-212. 如图,在直角坐标系xOy中,点A,B分别在x轴和y轴, . ∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是( )
A、4 B、-4 C、2 D、-212. 如图,在直角坐标系xOy中,点A,B分别在x轴和y轴, . ∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是( )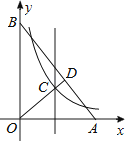 A、2 B、3 C、5 D、7
A、2 B、3 C、5 D、7二、填空题(每题4分,共24分)
-
13. 函数y= 中自变量x的取值范围是 .14. 如图,在平面直角坐标系中,已知点 , 以点O为圆心,长为半径画弧,交x轴的正半轴于点B , 则点B的横坐标为 .
 15. 已知点都在直线上,则 . (填“”“”或“”)16. 如图, 在平面直角坐标系 中, 四边形 是矩形, 点 分别在 轴、 轴上, 点 在函数 ( ) 的图象上, 边 与函数的图象相交于点 D,则阴影部分ODBC的面积为(结果用含k 的代数式表示).
15. 已知点都在直线上,则 . (填“”“”或“”)16. 如图, 在平面直角坐标系 中, 四边形 是矩形, 点 分别在 轴、 轴上, 点 在函数 ( ) 的图象上, 边 与函数的图象相交于点 D,则阴影部分ODBC的面积为(结果用含k 的代数式表示). 17. 如图,直线AB交反比例函数的图象于A,B两点,(点A,B在第一象限,且点在点的左侧),交轴于点 , 交轴于点 , 连结BO并延长交该反比例函数图象的另一支于点 , 连结AE交轴于点 , 连结BF,OA,且.
17. 如图,直线AB交反比例函数的图象于A,B两点,(点A,B在第一象限,且点在点的左侧),交轴于点 , 交轴于点 , 连结BO并延长交该反比例函数图象的另一支于点 , 连结AE交轴于点 , 连结BF,OA,且.
①若 , 则.
②若 , 则的值为.
18. 如图,一块砖的A,B,C三个面的面积比是4:2:1,如果 B面向下放在地上时,地面所受压强为a(Pa),那么 A面向下放在地上时,地面所受压强为Pa.
三、解答题(共7题,共78分)
-
19. 枣庄某公交车每天的支出费用为元,每天的乘车人数人与每天利润利润票款收入支出费用元的变化关系,如下表所示每位乘客的乘车票价固定不变:
人
元
根据表格中的数据,回答下列问题:
(1)、 是自变量;(2)、观察表中数据可知,当乘客量达到 人以上时,该公交车才不会亏损;(3)、请写出公交车每天利润元与每天乘车人数人的关系式: ;(4)、当一天乘客人数为多少人时,利润是元?20. 在平面直角坐标系xOy中的位置如图所示.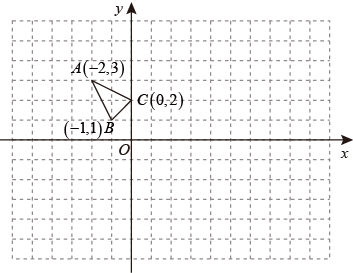
( 1 )作 关于点O成中心对称的 ;
( 2 )将 向右平移 个单位,作出平移后的 ;
( 3 )直接写出 各顶点坐标.
21. 两个水果市场各有芒果15吨,现从向甲、乙两地运送芒果,其中甲地需要芒果16吨,乙地需要芒果14吨,从到甲地的运费为50元/吨,到乙地的运费为30元/吨,从到甲地的运费为60元/吨,到乙地的运费为45元/吨.(1)、设地到甲地运送芒果吨,请完成下表:调往甲地(单位:吨)
调往乙地(单位:吨)
A
①
B
②
③
(2)、设总运费为元,请写出与的函数关系式,并直接写出的取值范围.(3)、怎样调送芒果才能使运费最少?22. 如图1,在平面直角坐标系中,直线分别与x轴、y轴相交于点A、B , 是的角平分线,交直线于点C .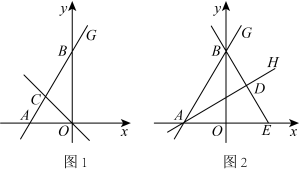 (1)、求点C的坐标;(2)、如图2,是的角平分线,过点B作的垂线交于点D , 交x轴于点E求直线的解析式;(3)、在x轴上寻找点F使得为等腰三角形,请直接写出点F的坐标.23. 如图,在平面直角坐标系中,一次函数 y=kx +b(k≠0)的图象与反比例函数的图象相交于 A(-1,2),B(m,-1)两点。
(1)、求点C的坐标;(2)、如图2,是的角平分线,过点B作的垂线交于点D , 交x轴于点E求直线的解析式;(3)、在x轴上寻找点F使得为等腰三角形,请直接写出点F的坐标.23. 如图,在平面直角坐标系中,一次函数 y=kx +b(k≠0)的图象与反比例函数的图象相交于 A(-1,2),B(m,-1)两点。 (1)、求反比例函数和一次函数的表达式.(2)、过点 B作直线l∥y轴,过点 A 作AD⊥l 于点D,C是直线l上一动点,若 DC=2DA,求点 C的坐标.24. 某公司要印制宣传材料,甲、乙两个印刷厂可选择,甲印刷厂只收取印制费,乙印刷厂收费包括印制费和制版费.
(1)、求反比例函数和一次函数的表达式.(2)、过点 B作直线l∥y轴,过点 A 作AD⊥l 于点D,C是直线l上一动点,若 DC=2DA,求点 C的坐标.24. 某公司要印制宣传材料,甲、乙两个印刷厂可选择,甲印刷厂只收取印制费,乙印刷厂收费包括印制费和制版费. (1)、甲印刷厂每份宣传材料的印制费是元;(2)、求乙印刷厂收费y(元)关于印制数量x(份)的函数表达式,并说明一次项系数,常数项的实际意义;y/元(3)、若印制相同数量,乙印刷厂的收费总是低于甲厂,求印制数量的范围.25. 某水果生产基地在气温较低时,用装有恒温系统的大棚栽培一种新品种水果,如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度与时间之间的函数关系,其中线段、表示恒温系统开启后阶段,双曲线的一部分表示恒温系统关闭阶段 .
(1)、甲印刷厂每份宣传材料的印制费是元;(2)、求乙印刷厂收费y(元)关于印制数量x(份)的函数表达式,并说明一次项系数,常数项的实际意义;y/元(3)、若印制相同数量,乙印刷厂的收费总是低于甲厂,求印制数量的范围.25. 某水果生产基地在气温较低时,用装有恒温系统的大棚栽培一种新品种水果,如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度与时间之间的函数关系,其中线段、表示恒温系统开启后阶段,双曲线的一部分表示恒温系统关闭阶段 .请根据图中信息解答下列问题:
 (1)、这个恒温系统设定的恒定温度为多少;(2)、求全天的温度与时间之间的函数表达式;(3)、若大棚内的温度低于时,蔬菜会受到伤害.问:这天内恒温系统最多可以关闭多少小时,才能避免水果生长受到影响?
(1)、这个恒温系统设定的恒定温度为多少;(2)、求全天的温度与时间之间的函数表达式;(3)、若大棚内的温度低于时,蔬菜会受到伤害.问:这天内恒温系统最多可以关闭多少小时,才能避免水果生长受到影响?